就活学生に送ったオファーの承認率を予測してみた
このブログはAidemy Premiumのカリキュラムの一環で、受講修了条件を満たすために公開しています
自己紹介
大阪の中小企業で、新卒採用業務をしています。
採用業務をする中で、データ分析に興味を持ち、Aidemyを受講しました。
分析を行ったきっかけ・目的
私が勤める企業は、大阪を拠点にマンション開発を手掛けるデベロッパーです。私はその会社で新卒採用を担当しています。
新卒採用における近年の課題は「集客が難しくなってきていること」です。
特に弊社は建築業界でもあるので、就活の早期化と他社との学生の奪い合いが熾烈で、学生獲得に苦戦していました。
そんな中でよく利用していたサービスが、「オファー」と呼ばれるようなメッセージを学生に送り、オファー内容を見た学生に「承認」されれば学生とやり取りができるというサービスです。(興味がなく、辞退されたりスルーされると、「非承認」となります。)
弊社に興味がありそうな学生を検索し、学生のプロフィールを見ては、オファーメッセージを送り続けるという日々を送っているのですが、良い時でも承認率は20%ほどなので、送る学生を間違えれば、多くの時間が無駄になりかねません。
そこで、機械学習を用いて、過去の送付実績をもとにこれから送る学生の承認率をある程度予測できないかと考えました。
実行環境
google colaboratory
Python3.10.12
目次
1.過去の送付データを取得
2.データの可視化
2-1.データ型の変換・統計量の出力
2-2.訓練データとテストデータに分割する
2-3.訓練データと検証データの内容の確認
①性別
2-4.相関の有無の確認
①数値データとの相関の可視化
②「性別」データとの相関の可視化
③「送信者性別」データとの相関の可視化
④「オファー月」ごとの承認有無の可視化
⑤「オファー曜日」ごとの承認有無の割合の可視化
⑥エリアごとの承認有無の割合の可視化
⑦国公私立ごとの承認有無の割合の可視化
⑧「文系/理系」ごとの承認有無の割合の可視化
3.文字列データを数値化
4.教師あり学習(二項分類)でモデルを学習
4-1.ロジスティック回帰の実行
4-2.正解率の高さの原因を探る
検証①学習にあまり関係しない要素を削除して学習させてみる
検証②:過学習を防ぐため、正則化を行う
検証③:データの偏りをなくす
検証③-1アンダーサンプリング
検証③-2 重みづけ
検証③-3 特定のエリアを抽出して予測する
5.モデルの予測
6.まとめ・反省
データセットについて
オファーメッセージを送った学生について、以下の情報が得られました。
承認の有無
オファー年
オファー月
オファー曜日
オファー時間(時)
学生の性別
居住エリア
学校区分
国公私立
専攻(文理)
文系/理系
志望業界1
志望職種1
志望企業タイプ
送信者性別
この15項目をもとに、学生の承認有無を予測していきます。
1.過去の送付データを取得
まずは、CSVファイルを取り込み、データサイズを確認します。
import numpy as np
import pandas as pd
from google.colab import drive
# Googleドライブをマウント
drive.mount('/content/drive')
# ファイルパスを指定してデータを読み込む例
data_df = '/content/drive/My Drive/最終課題/offerlist_all_2.csv'
data = pd.read_csv(data_df,encoding='cp932')
sample_data = data.iloc[:3867, :]
# データの先頭部分を表示
print(sample_data.head())
# 抽出したデータのサイズを確認
print("Sample data shape:", sample_data.shape)
print(f'{sample_data.dtypes} \n')
display(sample_data.head())


3,866名の学生データがありました。

2.データの可視化
2-1.データ型の変換・統計量の出力
文字列データをstr型に変えて、それぞれの統計量を出力します。
sample_data = sample_data.astype(
{
'オファー曜日' : str,
'性別':str,
'エリア' : str,
'学校区分':str,
'国公私立':str,
'専攻(文理)':str,
'文系/理系':str,
'志望業界1':str,
'志望職種1':str,
'志望企業タイプ':str,
'送信者性別' : str
}
)
# 数値データの統計量を表示
display(sample_data.describe())
# カテゴリカルデータの統計量を表示
display(sample_data.describe(exclude='number'))

「オファー年」の項目のminが2020.000000、maxが2024.000000であることから、2020~2024年のデータが含まれていることが分かります。

また、上記出力結果より、どの項目も3866個のデータがあることが分かります。
これにより、欠損値は無いことが確認できました。
2-2.訓練データとテストデータに分割する
日本語の文字列データが多い為、日本語対応させます。
!pip install japanize_matplotlib
import japanize_matplotlib全てのデータを訓練データとテストデータに分割後、「set」という項目で訓練データには0を、テストデータには1をラベリングします。
そして、再度2つのデータを統合します。
from sklearn.model_selection import train_test_split
# データを訓練データとテストデータに分割
train_data,test_data = train_test_split(sample_data, test_size=0.2, random_state=42)
# 各データセットのサイズを確認
print("Train data size:", len(train_data))
print("Test data size:", len(test_data))
# 識別項目の追加
train_data['set'] = 0
test_data['set'] = 1
# 訓練データとテストデータを再結合
all_data = pd.concat([train_data, test_data])
2-3.訓練データと検証データの内容の確認
訓練データの検証データの内容に大きな差が無いかを確認していきます。
①性別
性別ごとに、訓練データと検証データの個数を可視化してみます。
import seaborn as sns
# 男女別 訓練データと検証データの個数
sns.countplot(x='性別', hue='set', data=all_data)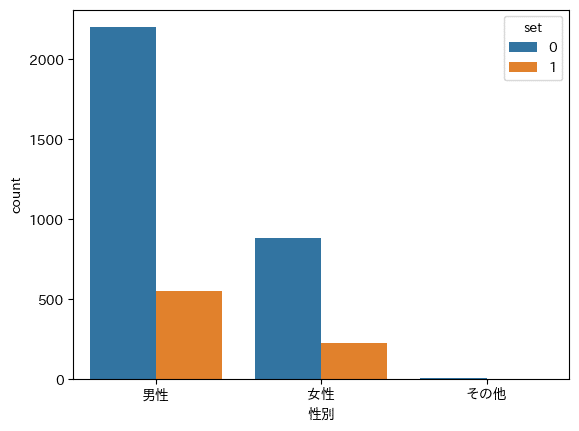
性別によって数に差があるため、比率が分かりにくい結果となってしまいました。
そこで、それぞれの割合を求めて可視化を行うことにしました。
import matplotlib.pyplot as plt
# '性別'カラムの各値の数をカウント
gender_counts = all_data['性別'].value_counts()
# 性別カラムの割合を計算
train_gender_counts = train_data['性別'].value_counts(normalize=True) * 100
test_gender_counts = test_data['性別'].value_counts(normalize=True) * 100
# 訓練データと検証データの割合をデータフレームに統合
ratios_df = pd.DataFrame({
'訓練データ': train_gender_counts,
'検証データ': test_gender_counts
}).T
# NaNを0に変換
ratios_df = ratios_df.fillna(0)
# グラフ作成
ax = ratios_df.plot(kind='bar', stacked=True, figsize=(10, 6))
ax.set_ylabel('割合 (%)')
ax.set_title('訓練データと検証データの性別割合')
ax.legend(title='性別', loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
plt.show()
訓練データと検証データの内容にほぼ相違は無いことが確認できました。
2-4.相関の有無の確認
①数値データとの相関の可視化
承認有無と、数値データである「オファー年」「オファー月」「オファー時間(時)」にそれぞれ相関があるかをヒートマップで可視化してみます。
sns.heatmap(
train_data[['承認有無','オファー年','オファー月','オファー時間(時)']].corr(),
vmax=1,vmin=-1,annot=True
)
残念ながら、承認有無と各項目に相関は無さそうでした。
import seaborn as sns
#男女別 承認なし、承認有の数
sns.countplot(x='性別', hue='承認有無', data=train_data)②「性別」データとの相関の可視化
import matplotlib.pyplot as plt
# 性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['性別', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.xlabel('性別')
plt.ylabel('割合 (%)')
plt.title('男女別の承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
③「送信者性別」データとの相関の可視化
import matplotlib.pyplot as plt
# 送信者性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['送信者性別', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('送信者性別ごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
④「オファー月」ごとの承認有無の可視化
import matplotlib.pyplot as plt
# 「オファー月」ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['オファー月', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('オファー月ごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
月ごとに若干の変動があります。
⑤「オファー曜日」ごとの承認有無の割合の可視化
import matplotlib.pyplot as plt
# 送信者性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['オファー曜日', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('オファー曜日ごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
明らかに土曜日と日曜日に送っているオファーの承認割合が高いことが分かります。
⑥エリアごとの承認有無の割合の可視化
import matplotlib.pyplot as plt
# 送信者性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['エリア', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('エリアごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=90)
承認が全くない/低いエリアがあることが分かりました。
⑦国公私立ごとの承認有無の割合の可視化
import matplotlib.pyplot as plt
# 送信者性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['国公私立', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('国公私立分類ごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
それぞれに大きな差は無さそうです。
⑧「文系/理系」ごとの承認有無の割合の可視化
import matplotlib.pyplot as plt
# 送信者性別ごとの承認有無のカウントを計算
approval_counts = train_data.groupby(['文系/理系', '承認有無']).size().unstack(fill_value=0)
# 承認割合を計算
approval_ratios = approval_counts.div(approval_counts.sum(axis=1), axis=0) * 100
# カラムの順序を変更して、「承認」を下に、「非承認」を上にする
approval_ratios = approval_ratios[[1, 0]]
# グラフ作成
approval_ratios.plot(kind='bar', stacked=True, figsize=(10, 6),color=['blue', 'lightgray'])
plt.ylabel('割合 (%)')
plt.title('文系/理系ごとの承認割合')
plt.legend(title='承認有無', labels=['承認あり', '承認無し'], loc='upper left', bbox_to_anchor=(1, 1))
plt.xticks(rotation=0)
「理系」は承認率が少し低く、「その他」は承認率が少し高い傾向があることが分かります。
3.文字列データを数値化
文字列データを数値に変換し、訓練データと検証データに分割します。
項目が複数ありますので、データを標準化しておきます。
※データの標準化とは:平均が0で分散が1のデータに変換すること。異なる項目のデータであっても同じように比較することができるようになります。
# 文字列で構成されるカラムをOne-Hot_Encodingで数値に変換
all_data_1 = pd.get_dummies(all_data, columns= ['オファー曜日','オファー時間(時)','専攻(文理)',
'志望職種1', "エリア","国公私立","学校区分","文系/理系","志望業界1", "志望企業タイプ",
"性別","送信者性別"])
# 前処理を施したall_dataを訓練データとテストデータに分割
train = all_data_1[all_data_1['set']==0]
test = all_data_1[all_data_1['set']==1].reset_index(drop=True)
#説明変数
df_x = train.drop(['承認有無'], axis=1)
#目的変数
df_y = train["承認有無"]
#文字列型のデータを数値型(0-1)に変換
df_x = pd.get_dummies(df_x)
#欠損値を処理する
df_x = df_x.fillna(0)
#標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
pd.DataFrame(scaler.fit_transform(df_x),
columns=df_x.columns)

4.教師あり学習(二項分類)でモデルを学習
アルゴリズムを選択します。
今回の分析では、「承認」と「非承認」の二項分類を行いたいので、
教師あり学習(分類)の手法を用います。
まずは、ロジスティック回帰で分析を行うことにしました。
4-1.ロジスティック回帰の実行
#ロジスティック回帰
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
X_train, X_val, y_train, y_val = train_test_split(df_x, df_y, test_size=0.2, random_state=42)
# モデルを定義し学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率を計算
accuracy = accuracy_score(y_val, y_pred)
print("正解率:", accuracy)
正解率: 0.9176090468497576
accuracy(正解率)が異様に高いのが気になります。
この原因について、3つの予測を行うことにしました。
予測①:学習に関わる要素の数が多すぎる
予測②:過学習している
予測③:データに偏りがある
3つの予測に対応して、3つの検証を行います。
検証①:学習にあまり関係しない要素を削除して学習させてみる
検証②:過学習を防ぐため、正則化を行う
検証③:データの偏りをなくす
4-2.正解率の高さの原因を探る
検証①:学習にあまり関係しない要素を削除して学習させてみる
まずは、関係する係数を出力します。
下記コードの
model.coef_では、y=ax+bの「a」を、
model.intercept_では、y=ax+bの「b」を予測しています。
print(model.coef_, model.intercept_)▼出力結果
[[-8.48896439e-04 -5.82943341e-02 0.00000000e+00 5.41877057e-01 5.63632671e-01 -2.32459158e-01 -4.08712814e-01 -1.39144557e-01 -2.32078286e-01 -9.41784534e-02 5.62855078e-01 -1.12790495e-02 -1.95139175e-01 2.90851839e-01 4.35249239e-01 1.41549825e-01 -4.29005691e-01 -9.51752415e-02 2.12449882e-01 -6.53588731e-02 -8.09835642e-01 -3.82257320e-02 7.84915499e-02 -2.51564993e-01 -5.16508639e-01 -1.56135658e-01 -1.11094276e-01 -3.45968498e-01 2.54850993e-01 2.48852354e-01 -9.98262881e-01 -9.14827624e-02 3.18788911e-01 4.42944387e-02 -5.48108244e-01 2.71928861e-01 6.52979360e-01 3.94604177e-01 6.29230387e-02 4.20077792e-01 6.11049538e-02 2.84275820e-01 2.62323119e-01 -2.27157433e-01 -3.35242104e-01 4.43927114e-02 2.03326451e-02 -3.93814580e-02 7.47336842e-02 0.00000000e+00 1.24888996e-01 0.00000000e+00 -2.33607929e-02 -2.59977181e-02 2.39341018e-01 1.63951845e-01 -1.84556705e-01 -1.22230268e-02 -1.23735387e-01 -2.95422817e-02 6.47163889e-01 -4.92477401e-02 -1.63323230e-01 -7.70949180e-02 -2.03328493e-02 -6.07255069e-02 -1.30965190e-01 2.13466084e-01 2.25451738e-02 -9.51463532e-02 -3.16575243e-02 -1.49030421e-01 5.56866518e-01 1.36361755e-01 0.00000000e+00 -1.37033054e-01 -7.39294992e-01 -2.80867642e-01 0.00000000e+00 -1.91775954e-01 1.17118984e-02 -3.05557889e-02 -6.72614196e-02 -1.94838864e-02 -1.05399156e-01 -4.02873658e-02 -5.55267000e-01 8.02123991e-01 4.24365377e-01 2.02790532e-01 1.12989630e-01 -2.22949447e-01 -1.02677891e-01 -7.52321498e-02 2.10284139e-01 -1.04688002e-02 2.28058344e-01 -5.39311117e-01 6.79453534e-01 -6.12345795e-01 -4.55560525e-01 5.20577407e-01 -8.59323569e-02 -6.43835717e-02 1.99458248e-01 1.39391092e-01 -7.48523719e-02 9.18337868e-02 -1.72851608e-01 1.54806652e-01 -6.73230604e-02 6.46847297e-02 2.10224924e-02 1.14781799e-01 8.96845417e-02 -6.91135994e-02 -2.07442815e-02 -1.34056162e-01 7.84915499e-02 1.41758971e-02 -9.37309886e-02 -5.72994690e-01 2.55604282e-01 8.95785988e-01 1.37443708e-02 -2.41968730e-02 -7.63090412e-03 -1.66541816e-01 2.30173662e-02 2.03029564e-01 -2.77516035e-01 -5.21390065e-02 -1.89112752e-01 -7.24701521e-02 0.00000000e+00 3.22165090e-01 1.90474798e-01 -3.82723761e-01 -2.26668586e-01 7.98209101e-01 6.83972690e-01 -1.59553271e-01 -9.01330392e-02 2.44559124e-01 -1.80428117e-01 6.92576090e-01 -2.73435080e-01 -1.27369689e-01 1.02155462e-01 -3.44127949e-01 -8.29458286e-02 2.32775018e-02 -2.81698104e-01 3.65570675e-02 4.10801556e-01 -7.41519672e-02 3.03798748e-02 -4.06162041e-02 -3.01307295e-01 -1.15620979e-01 8.58852296e-02 1.66622296e-01 -1.22612774e-01 1.22248747e-01 -1.17407961e-01 4.48127398e-01 -2.32656726e-01 -1.65921163e-01 -3.38736915e-01 -1.28306691e-01 -7.48526890e-01 -1.12564807e-01 -1.86777590e-01 1.71691381e-01 3.89256991e-01 -1.14311895e-01 -2.08596475e-01 6.83318107e-01 2.46245937e-02 -2.50815867e-01 -1.87788760e-01 3.01595421e-01 1.58711323e-01 6.03416434e-01 -3.74064913e-01 -2.27505795e-01 -3.83201310e-01 -2.11148108e-03 2.90446037e-01 -3.94984989e-01 -3.33786669e-01 2.99680802e-01 -1.56786627e-01 1.07439629e-01 4.82834558e-02 -1.02411488e-01 1.01347946e-01]] [-0.00120057]
係数を出力しただけだと、何がどう影響しているのかが分からないので、この出力結果を可視化していきます。
df_coef = pd.DataFrame(model.coef_.T, index=df_x.columns, columns=['coef'])
df_coef.plot.barh(figsize=(8,40))
影響が少ない=係数の絶対値が0.25以下と定義して見ていくと、
「送信者性別」,「性別」,「文系/理系」,「学校区分」,「国公私立」,「オファー月」,「オファー年」が該当しました。
この項目のカラムを削除し、もう一度ロジスティック回帰を行います。
drop_col=['送信者性別','性別','文系/理系','学校区分','国公私立','オファー月','オファー年']
all_data_2 = all_data.drop(drop_col, axis=1)
all_data_2 = pd.get_dummies(all_data_2, columns
= ['オファー曜日','オファー時間(時)','志望業界1','志望職種1',
'専攻(文理)','志望企業タイプ','エリア'])from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# 前処理を施したall_dataを訓練データとテストデータに分割
train_2 = all_data_2[all_data_2['set']==0]
test_2 = all_data_2[all_data_2['set']==1].reset_index(drop=True)
#説明変数
df_x_2 = train_2.drop(['承認有無'], axis=1)
#目的変数
df_y_2 = train_2["承認有無"]
#欠損値を処理する
df_x_2 = df_x_2.fillna(0)
#標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
pd.DataFrame(scaler.fit_transform(df_x_2),
columns=df_x_2.columns)
X_train2, X_val2, y_train2, y_val2 = train_test_split(df_x_2, df_y_2, test_size=0.2, random_state=42)
# モデルを定義し学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train2, y_train2)
# モデルの予測
y_pred2 = model.predict(X_val2)
#正解率を計算
accuracy2 = accuracy_score(y_val2, y_pred2)
print("正解率:", accuracy2)
正解率: 0.9159935379644588
相変わらず正解率は値が高いままでした。
検証②:過学習を防ぐため、正則化を行う
過学習を防ぐため、L1正則化・L2正則化を行っていきます。
L1正則化:「予測に影響を及ぼしにくいデータ」にかかる係数をゼロに近づける手法です。主に余分な情報がたくさん存在するようなデータの回帰分析を行う際に用います。
L2正則化:係数が大きくなりすぎないように制限する手法であり、過学習を抑えるために用いられます。
#L1正則化
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# データをトレーニングセットとテストセットに分割
X_train, X_val, y_train, y_val = train_test_split(df_x_2, df_y_2, test_size=0.2, random_state=42)
# モデルを定義し学習(L1正則化を使用)
model = LogisticRegression(penalty='l1', solver='liblinear',C=0.1, max_iter=1000)
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率を計算
accuracy = accuracy_score(y_val, y_pred)
print("正解率:", accuracy)
正解率: 0.9176090468497576
#L2正則化
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
# データをトレーニングセットとテストセットに分割
X_train, X_val, y_train, y_val = train_test_split(df_x_2, df_y_2, test_size=0.2, random_state=42)
# モデルを定義し学習(L2正則化を使用)
model = LogisticRegression(penalty='l2', solver='lbfgs', max_iter=1000)
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率を計算
accuracy = accuracy_score(y_val, y_pred)
print("正解率:", accuracy)
正解率: 0.9159935379644588
2つの正則化を行った後でも、accuracyにほとんど変化はありませんでした。
検証③:データの偏りをなくす
実際のデータの偏りについて確認していきます。
#元データの承認有無のデータの偏りについて確認
print(sample_data["承認有無"].value_counts())
print(sample_data["承認有無"].value_counts(normalize=True))
約9:1で非承認が多いことが分かります。
y_pred # 予測結果array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,・・・・・
と、全ての結果が出力されました。
このことから、非承認の割合が高いために、全て非承認(0)と予測するだけでaccuracyが高い数値を出力するようになっていたと考えられます。
この分析では、承認(1)を予測できないと意味がないので、これ以降はaccuracyだけでなく、適合率と再現率、F1スコアも算出することにしました。
正解率(Accuracy):予測結果全体がどれくらい真の値と一致しているかを表す指標
適合率(Presision):正と判定した結果のうち、実際に真の値と一致しているかを表す 指標
再現率(Recall):実際に正であるものの中から、どれだけ正と予測できたかを表 す指標で、網羅率を意味する指標
F1スコア:適合率と再現率の調和平均
検証③-1アンダーサンプリング
そして、承認と非承認の割合の偏りを無くすために、アンダーサンプリングを行いました。
アンダーサンプリング:多数派のデータ数を少数派のデータ数に合わせて削減すること。
今回は、0(非承認)をランダムに削除し、1(承認)の数と同数になるようにしました。
#アンダーサンプリングの為のデータ作成
# 1と0のカウント
count_1 = sample_data['承認有無'].value_counts()[1]
count_0 = sample_data['承認有無'].value_counts()[0]
# 0のデータをランダムに削除して1と0の比率を1:1にする
if count_1 > count_0:
sample_data_balanced = pd.concat([
sample_data[sample_data['承認有無'] == 1].sample(n=count_0, random_state=42),
sample_data[sample_data['承認有無'] == 0]
])
else:
sample_data_balanced = pd.concat([
sample_data[sample_data['承認有無'] == 1],
sample_data[sample_data['承認有無'] == 0].sample(n=count_1, random_state=42)
])
# 結果の確認
print("元のデータのカウント:")
print(sample_data['承認有無'].value_counts())
print("\nバランス調整後のデータのカウント:")
print(sample_data_balanced['承認有無'].value_counts())
アンダーサンプリングを行ったデータを用いて、機械学習の前処理を行っていきます。
#アンダーサンプリングをしたデータを用いて、機械学習の準備
from sklearn.model_selection import train_test_split
# データを訓練データとテストデータに分割
train_data,test_data = train_test_split(sample_data_balanced, test_size=0.2, random_state=42)
# 各データセットのサイズを確認
print("Train data size:", len(train_data))
print("Test data size:", len(test_data))
# 識別項目の追加
train_data['set'] = 0
test_data['set'] = 1
# 訓練データとテストデータを再結合
balanced_data = pd.concat([train_data, test_data])
print(balanced_data.head())
▲出力結果
訓練データは587、検証データは147あります。
更に文字列データの数値化・標準化等を行います。
# 文字列で構成されるカラムをOne-Hot_Encodingで数値に
balanced_data = pd.get_dummies(balanced_data, columns= ['オファー曜日','オファー時間(時)','専攻(文理)',
'志望職種1', "エリア","国公私立","学校区分","文系/理系","志望業界1", "志望企業タイプ",
"性別","送信者性別"])
# 前処理を施したall_dataを訓練データとテストデータに分割
train = balanced_data[all_data_1['set']==0]
test = balanced_data[all_data_1['set']==1].reset_index(drop=True)
#説明変数
df_x_3 = train.drop(['承認有無'], axis=1)
#目的変数
df_y_3 = train["承認有無"]
#文字列型のデータを数値型(0-1)に変換
df_x_3 = pd.get_dummies(df_x_3)
#欠損値を処理する
df_x_3 = df_x_3.fillna(0)
#標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
pd.DataFrame(scaler.fit_transform(df_x_3),
columns=df_x_3.columns)再度、ロジスティック回帰を行います。
#ロジスティック回帰(承認:非承認が1:1の時)
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
X_train3, X_val3, y_train3, y_val3 = train_test_split(df_x_3, df_y_3, test_size=0.2, random_state=42)
# モデルを定義し学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train3, y_train3)
# モデルの予測
y_pred3 = model.predict(X_val3)
# 正解率・適合率・再現率・F1スコアを計算
accuracy = accuracy_score(y_val3, y_pred3)
print('正解率:Accuracy = ', accuracy_score(y_val3, y_pred3))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy = 0.5254237288135594
適合率:Precision = 0.0
再現率:Recall = 0.0
F1 score = 0.0
正解率は下がりましたが、その他の値が0.0なので、更に正則化を行っていきます。
#L1正則化
# モデルを定義し学習(L1正則化を使用)
model = LogisticRegression(penalty='l1', solver='liblinear',C=0.1, max_iter=1000)
model.fit(X_train3, y_train3)
# モデルの予測
y_pred = model.predict(X_val3)
# 正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy = ', accuracy_score(y_val3, y_pred3))
print('適合率:Precision = ', precision_score(y_val3, y_pred3))
print('再現率:Recall = ', recall_score(y_val3, y_pred3))
print('F1 score = ', f1_score(y_val3, y_pred3))正解率:Accuracy = 0.5254237288135594
適合率:Precision = 0.5074626865671642
再現率:Recall = 0.5964912280701754
F1 score = 0.5483870967741935
#L2正則化
# モデルを定義し学習(L2正則化を使用)
model = LogisticRegression(penalty='l2', solver='lbfgs', max_iter=1000)
model.fit(X_train3, y_train3)
# モデルの予測
y_pred = model.predict(X_val3)
# 正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy = ', accuracy_score(y_val3, y_pred3))
print('適合率:Precision = ', precision_score(y_val3, y_pred3))
print('再現率:Recall = ', recall_score(y_val3, y_pred3))
print('F1 score = ', f1_score(y_val3, y_pred3))正解率:Accuracy = 0.5254237288135594
適合率:Precision = 0.5074626865671642
再現率:Recall = 0.5964912280701754
F1 score = 0.5483870967741935
正則化を行うことで、正解率に変化はありませんでしたが、適合率・再現率・F1 scoreは向上しました。
検証③-2 重みづけ
データに偏りがある場合、少数派のデータに重みづけを行うことで現実的で信頼性の高い結果を得られることがあるようです。
アンダーサンプリング前のデータを用いて、この重みづけの手法も試してみることにしました。
#ロジスティック回帰(重みづけ有り)
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
X_train, X_val, y_train, y_val = train_test_split(df_x, df_y, test_size=0.2, random_state=42)
# モデルを定義し学習
model = LogisticRegression(max_iter=1000,class_weight='balanced')
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy ', accuracy_score(y_val, y_pred))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy 0.5993537964458805
適合率:Precision = 0.08085106382978724
再現率:Recall = 0.37254901960784315
F1 score = 0.1328671328671329
#非線形SVM(重みづけ有り)
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
# モデルの構築
model = SVC(class_weight='balanced')
# モデルの学習
model.fit(X_train, y_train)
# 正解率の算出
model.score(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
#正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy', accuracy_score(y_val, y_pred))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy 0.9176090468497576
適合率:Precision = 0.0
再現率:Recall = 0.0
F1 score = 0.0
#決定木(重みづけあり)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
# モデルの構築
model = DecisionTreeClassifier(class_weight='balanced')
# モデルの学習
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy', accuracy_score(y_val, y_pred))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy 0.8239095315024233
適合率:Precision = 0.11842105263157894
再現率:Recall = 0.17647058823529413
F1 score = 0.14173228346456693
#ランダムフォレスト(重みづけあり)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
# モデルの構築
model = RandomForestClassifier(class_weight='balanced')
# モデルの学習
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率・適合率・再現率・F1スコアの計算
print('正解率:Accuracy', accuracy_score(y_val, y_pred))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy 0.9159935379644588
適合率:Precision = 0.0
再現率:Recall = 0.0
F1 score = 0.0
#K近傍法(重みづけあり)
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, random_state=42)
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
# モデルの構築
model = KNeighborsClassifier(n_neighbors=10,weights='distance')
# モデルの学習
model.fit(X_train, y_train)
# モデルの予測
y_pred = model.predict(X_val)
# 正解率・適合率・再現率・F1スコアを計算
print('正解率:Accuracy ', accuracy_score(y_val, y_pred))
print('適合率:Precision = ', precision_score(y_val, y_pred))
print('再現率:Recall = ', recall_score(y_val, y_pred))
print('F1 score = ', f1_score(y_val, y_pred))正解率:Accuracy 0.9159935379644588
適合率:Precision = 0.0
再現率:Recall = 0.0
F1 score = 0.0
この中だと、決定木を使って学習した予測モデルが一番精度が高そうです。
検証③-3 特定のエリアを抽出して予測する
データの偏りにより、正解率が以上に高い数値になっていたので、偏りを少なくするため、承認率が高い項目でデータを絞り、学習をさせてみることにしました。
弊社は大阪にしか事業所が無い企業ですので、「近畿地区」に住んでいる学生からの承認率は高いと予測しました。
そこで、「近畿地区」のデータのみを抽出し、実際の割合を確認します。
#承認率が高いであろう「近畿地区」のデータのみを抽出
kinki_area_data = sample_data[all_data['エリア'] == '近畿地区']
#近畿地区のデータの承認有無の数と割合を確認
print(kinki_area_data["承認有無"].value_counts())
print(kinki_area_data["承認有無"].value_counts(normalize=True))
全てのデータと比較すると、少しではありますが承認率が高いことが分かります。(全国:0.09493 近畿地区:0.103759)
試しに近畿地区で学習します。
from sklearn.model_selection import train_test_split
# データを訓練データとテストデータに分割
train_data_kinki,test_data_kinki = train_test_split(kinki_area_data, test_size=0.2, random_state=42)
# 各データセットのサイズを確認
print("Train data size:", len(train_data_kinki))
print("Test data size:", len(test_data_kinki))
# 識別項目の追加
train_data_kinki['set'] = 0
test_data_kinki['set'] = 1
# 訓練データとテストデータを再結合
all_data_kinki = pd.concat([train_data_kinki, test_data_kinki])
print(all_data_kinki.head())
# 前処理を施したall_dataを訓練データとテストデータに分割
train_kinki = all_data_kinki[all_data_kinki['set']==0]
test_kinki = all_data_kinki[all_data_kinki['set']==1].reset_index(drop=True)
#説明変数
df_x_kinki = train_kinki.drop(['承認有無'], axis=1)
#目的変数
df_y_kinki = train_kinki["承認有無"]
#文字列型のデータを数値型(0-1)に変換
df_x_kinki = pd.get_dummies(df_x_kinki)
#欠損値を処理する
df_x_kinki = df_x_kinki.fillna(0)
#標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
pd.DataFrame(scaler.fit_transform(df_x_kinki),
columns=df_x_kinki.columns)
Train data size: 2128
Test data size: 532
from sklearn.model_selection import train_test_split
# データを訓練データとテストデータに分割
train_data_kinki,test_data_kinki = train_test_split(kinki_area_data, test_size=0.2, random_state=42)
# 各データセットのサイズを確認
print("Train data size:", len(train_data_kinki))
print("Test data size:", len(test_data_kinki))
# 識別項目の追加
train_data_kinki['set'] = 0
test_data_kinki['set'] = 1
# 訓練データとテストデータを再結合
all_data_kinki = pd.concat([train_data_kinki, test_data_kinki])
print(all_data_kinki.head())
# 前処理を施したall_dataを訓練データとテストデータに分割
train_kinki = all_data_kinki[all_data_kinki['set']==0]
test_kinki = all_data_kinki[all_data_kinki['set']==1].reset_index(drop=True)
#説明変数
df_x_kinki = train_kinki.drop(['承認有無'], axis=1)
#目的変数
df_y_kinki = train_kinki["承認有無"]
#文字列型のデータを数値型(0-1)に変換
df_x_kinki = pd.get_dummies(df_x_kinki)
#欠損値を処理する
df_x_kinki = df_x_kinki.fillna(0)
#標準化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
pd.DataFrame(scaler.fit_transform(df_x_kinki),
columns=df_x_kinki.columns)
#ロジスティック回帰
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
X_train_kinki, X_val_kinki, y_train_kinki, y_val_kinki = train_test_split(df_x_kinki, df_y_kinki, test_size=0.2, random_state=42)
# モデルを定義し学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train_kinki, y_train_kinki)
# モデルの予測
y_pred_kinki = model.predict(X_val_kinki)
# テストデータ(近畿圏)に対する正解率・適合率・再現率・F1スコアを計算
print('近畿圏のみのデータの場合')
print('正解率:Accuracy = ', accuracy_score(y_val_kinki, y_pred_kinki))
print('適合率:Precision = ', precision_score(y_val_kinki, y_pred_kinki))
print('再現率:Recall = ', recall_score(y_val_kinki, y_pred_kinki))
print('F1 score = ', f1_score(y_val_kinki, y_pred_kinki))近畿圏のみのデータの場合
正解率:Accuracy = 0.8943661971830986
適合率:Precision = 0.0
再現率:Recall = 0.0
F1 score = 0.0
正解率は高いですが、適合率や再現率、F1scoreは0.0と微妙な結果になってしまいました・・・。
その後、正則化も行いましたが、値に変化はありませんでした。
やはり、データの偏りがあまり解消しきれなかったのが原因かもしれません。
5.モデルの予測
以上の結果より、
アンダーサンプリングをした場合だと、ロジスティック回帰の正則化適用後
元のデータのまま場合だと、重みづけを施した決定木のモデルが一番正確に予測ができるということが分かりました。
それぞれのモデルを使って、テストデータの承認率を計算していきます。
①アンダーサンプリング後、ロジスティック回帰の正則化適用
# 承認(1)の割合を計算
percentage_of_ones = np.sum(y_pred == 1) / len(y_pred) * 100
print(f'承認率:{percentage_of_ones:.2f}%')承認率:56.78%
②重みづけを施した決定木のモデル
# 承認(1)の割合を計算
percentage_of_ones = np.sum(y_pred == 1) / len(y_pred) * 100
print(f'承認率:{percentage_of_ones:.2f}%')承認率:11.15%
アンダーサンプリングしたデータについては、承認と非承認が1:1になっている為、承認率も高くなっています。
やはり体感としては、重みづけを施した決定木のモデルが現実的だと感じました。
6.まとめ・反省
データの偏りが与える影響について最初は気づかず、正解率が不自然に高い原因を探るのに時間がかかってしまいました。
しかし、今回うまくいかないときの対処法や考え方を学べたことはとても貴重な体験になりました。
今後も機械学習やデータ分析を通して課題解決を行っていきたいと思います。
