FXを機械学習！〜重回帰分析〜

こんにちは！

前回はFXデータの単回帰分析を行いました。

今回は重回帰分析を行なっていきたいと思います。

単回帰分析と違うところは、説明変数が複数あるところです。

単回帰分析では、

目的変数　円/ドル

説明変数　先月の円/ドル

としましたが、

今回の重回帰分析では、

目的変数　円/ドル

説明変数　円/ドル、円/ユーロ

としました。

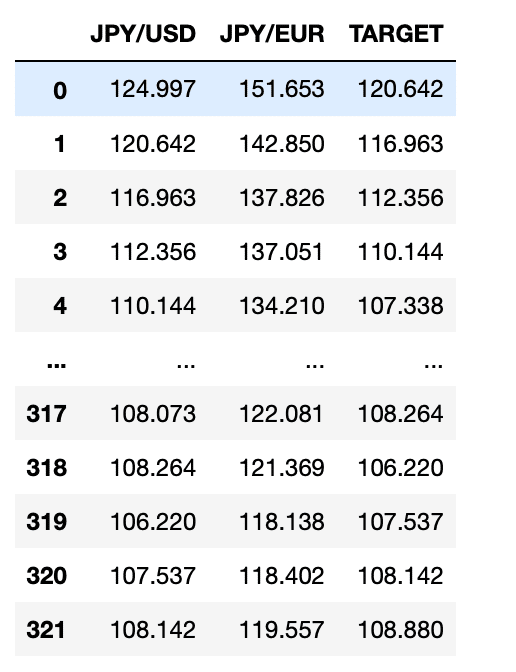
CSVから読み込んだデータがこちら

CSVデータ

これを３次元グラフに表すと、

3次元散布図

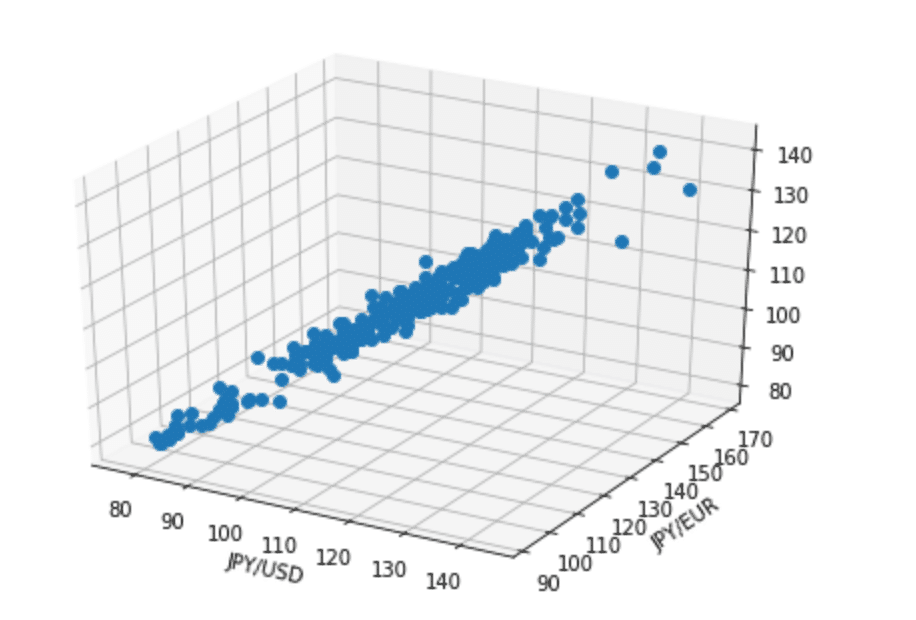
ここで重回帰分析を行なっていきます。
単回帰分析では直線で予測グラフが表されましたが、重回帰分析では平面（または超平面）で予測グラフが表されます。

今回は説明変数２つでの重回帰分析なので、
y=w0+w1x1+w2x2�=�0+�1�1+�2�2
という式で表されます。
x1は先月の円/ドル、x2は先月の円/ユーロです。
w0,w1,w2は学習された重みです。

学習の結果、
w0=3.70254341�0=3.70254341
w1=0.98374897�1=0.98374897
w2=−0.01556721�2=−0.01556721
となりました。

グラフ化すると、

予測グラフ

アングルの問題で平面に見えづらいですが、きれいにデータにそったグラフが描かれているのがわかります（オレンジが平面）。

また、予測精度であるMSEは

MSE=7.524662088736376���=7.524662088736376

となり、単回帰分析の時より精度が上がっているのがわかります。