産業保健職のための疫学・統計学‐データの分析手法：重回帰分析-2調整を視覚的に理解する

重回帰分析をイメージで理解していくための一連のシリーズの2本目の記事となります。ここでは、よく言われる「調整」が何を意味するかを見ていきましょう。

この記事のテーマとなるデータ

この記事では、次の散布図を見ながら、重回帰分析による調整が何を示しているかを考えていきましょう。x軸に足の大きさ、y軸に学力テストの点数をプロットしています。きれいな右肩上がりのグラフですね。読み進む前に、このグラフから読み取れることをちょっと考えてみてください。

はい、もし、足が大きいとテストの成績が上がる！と結論付けてしまった方がいたら、t検定の記事をもう一度読んでみてください。背景因子による調整というものを、分析するときには考える必要がありました。普通に考えると足の大きさとテストの点数が関係あるとは少し考えにくいです。

ただ、それでも一応重回帰分析を実施しましょう。今回の場合、点に対する直線の式は、$${(テストの点数)=\beta_0+\beta_1(足の大きさ)}$$となって、分析した結果、この点に対して、最も距離を短くできる$${\beta_0, \beta_1}$$は、$${\beta_0=-98.3735, \beta_1=8.4815}$$となりました。

これはこれで、データに対してはそれなりに特徴をとらえた線です。ただ、最初にも記載したように、この線は嘘っぱちです。

層別化して調整してみる

それでは、次のように、学年という提示していなかった情報で層別化（塗分けてみる）とどうでしょうか？全体としては右肩上がりですが、それぞれの塗分けられた色だけに着目すると、右肩上がりとはあまり言えなさそうです。

もう少しわかりやすく、各学年を別々のグラフとしてプロットしてみましょう。ここまで分解すると、点の集まり、学年別にみると足の大きさと学力テストの点数には何の関係もなさそうですね？

このように、学年で層別化すると、足の大きさと学力テストの点数に対して、6本の線が引けそうです。次に重回帰分析の式と分析結果が、実際に6本の線を引いているところを見てみましょう。

重回帰分析で調整してみる

もう一度調整前の式をみておきましょう。この分析では、足の大きさが1㎝大きくなると、学力テストの点数が8.4815上昇するというような結果でした。

これに対して、学年を考慮した式を考えると、次のようになります。

$$(テストの点数)=\beta_0+\beta_1(足の大きさ)+\beta_2(2年生)+\beta_3(3年生)+\beta_4(4年生)+\beta_5(5年生)+\beta_6(6年生)+\beta_7(7年生)$$

例で考えてみます。1年生で足の大きさが15㎝だった場合、式は、$${(テストの点数)=\beta_0+15\beta_1}$$となります。$${\beta_2\sim\beta7}$$は1年生のデータではすべてゼロになるので、消えています。他の学年も含めて、次のような形ですね

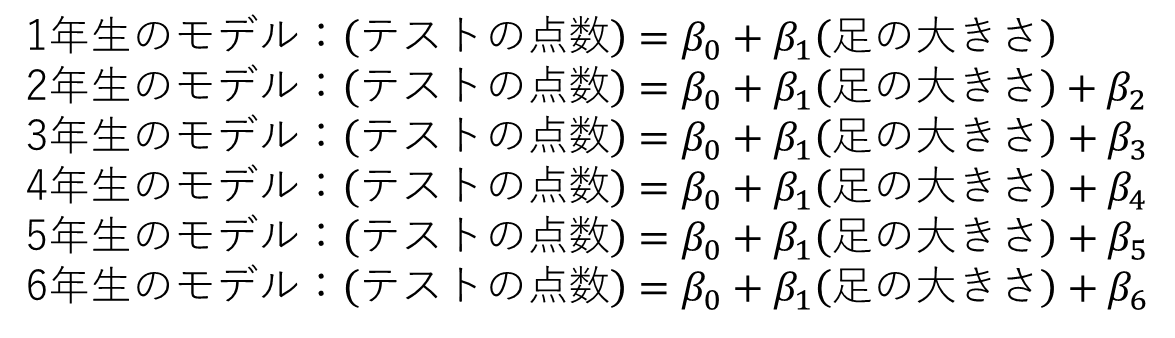
それで、この式の各々の$${\beta}$$を推定する重回帰分析を実施すると次のような結果になります。footの係数$${\beta_0}$$はほぼ0で、学年にかかっている係数が値が1学年増えるごとに増加しているので、足の大きさはテストの点数にはほぼ影響を与えていない一方で、学年が上がるごとにしっかりと点数が上昇していくというような結果です。

この係数を実際のデータに当てはめて線を引いてみると、次のような形です。このように、式が表現されることで、足の大きさの背景因子、学年を調整してテストの点数との関係を調べることができました。

まとめ

この記事では、重回帰分析で調整するということのイメージについて解説してきました。複数の直線を一つの直線で表すということができれば、このように、一つの結果（学力テスト）を二つの変数（足の大きさと学年）で調整して、その関係を紐解くことができます。

次の記事では重回帰分析のシリーズのまとめとして、実際にありそうな人事労務関係のデータ（私が作成した架空のデータです）を分析していくような過程を見ていきます。