
G検定 4-2 13. 誤差関数
シラバス 13. 誤差関数 をまとめていきます。
目標
・誤差関数の基礎的な知識を理解する
・代表的な誤差関数を理解する
・適用するタスクに応じて、適切な誤差関数を選択できる
キーワード
Contrastive loss, Triplet Loss, カルバック・ライブラー情報量 (KL), 交差エントロピー, 平均二乗誤差
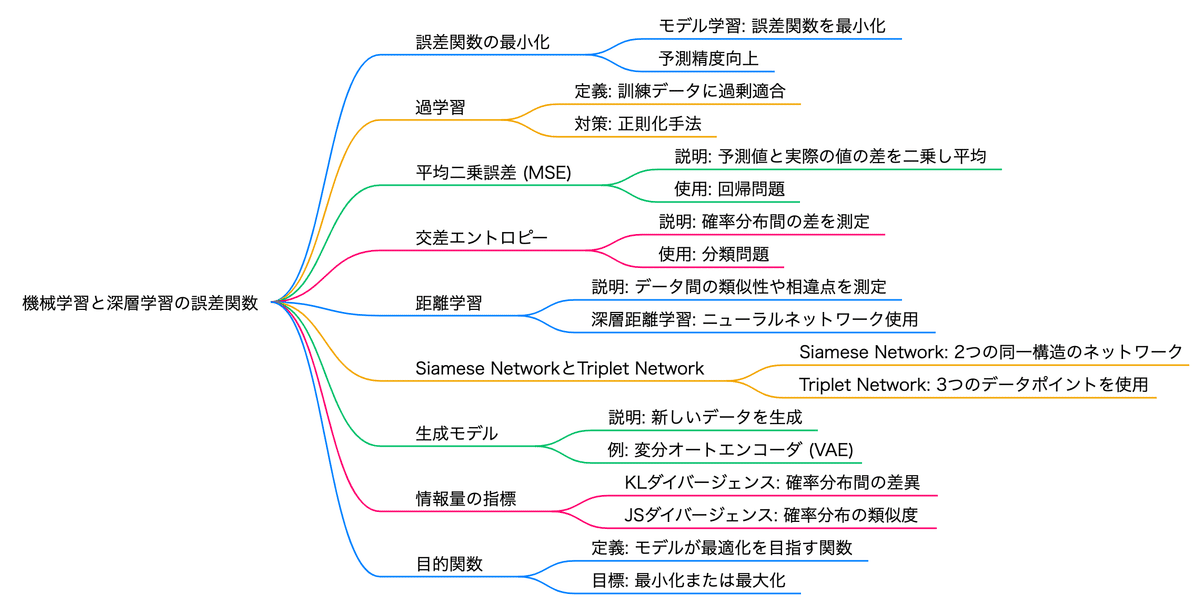
誤差関数(損失関数)とは?
誤差関数(損失関数)は、モデルの予測結果と実際の正解値(ground truth)との間の差を数値的に表現する関数です。この差を「損失」または「誤差」と呼びます。損失関数の値が小さいほど、モデルの予測が正確であることを意味します。ディープラーニングでは、この損失を最小化することを目的としてモデルのパラメータ(重みやバイアス)を調整します。
損失関数は、モデルの学習プロセスにおいて以下のような役割を果たします:
評価: モデルの性能を定量的に評価する。
最適化: 勾配降下法などの最適化アルゴリズムを用いて、損失を最小化する方向にパラメータを更新する。
誤差関数を最小化することでモデル学習が行われ、適切な予測ができるようになる。
過学習に注意が必要。
対応策は総じて正則化と呼ぶ。
損失関数の種類
損失関数は、主にタスクの種類(分類問題か回帰問題か)に応じて選択されます。以下に代表的な損失関数を分類ごとに紹介します。
1. 分類問題で使用される損失関数
分類問題では、モデルが各クラスの確率を予測し、その確率と正解ラベルとの間の誤差を測定します。
クロスエントロピー損失(Cross-Entropy Loss)
主に多クラス分類問題で使用される損失関数。
モデルが正しいクラスに高い確率を割り当てるほど損失が小さくなります。
ヒンジ損失(Hinge Loss)
サポートベクターマシン(SVM)などで使用される損失関数。
主に二値分類問題で利用され、マージンを最大化するようにモデルを訓練します。
2. 回帰問題で使用される損失関数
回帰問題では、モデルが連続値を予測し、その予測値と実際の値との誤差を測定します。
平均二乗誤差関数 (Mean Squared Error, MSE)
モデルが予測した値と実際の値の差を二乗し、平均を取ることで誤差を評価する関数です。
誤差が大きいほど値も大きくなり、小さくすることでモデルの性能を改善できます。
回帰問題の誤差関数として用いられることが多い
平均絶対誤差(Mean Absolute Error, MAE)
外れ値に対してMSEよりもロバスト(頑健)です
ハッバー損失(Huber Loss)
MSEとMAEの特性を組み合わせた損失関数。
外れ値に対してロバストでありながら、誤差が小さい場合にはMSEのように振る舞います。
損失関数の選択基準
損失関数を選択する際には、以下の点を考慮します:
タスクの種類: 分類問題か回帰問題か。
データの特性: 外れ値の有無やデータのスケール。
モデルの目的: 高い精度が必要か、ロバスト性が重要か。
例えば、外れ値が多いデータセットでは、MSEよりもMAEやハッバー損失が適しています。一方、分類問題ではクロスエントロピー損失が一般的に使用されます。
交差エントロピー (Cross Entropy)
損失関数(目的関数)で、分類タスクや確率的出力の評価に役立ちます。
確率分布間の差を測る方法で、特に分類問題でどれだけ予測が正確かを評価します。
交差エントロピー誤差関数 (Cross Entropy Loss)
交差エントロピーは、2つの確率分布の類似性を測る指標で、「真の確率分布」と「予測される確率分布」の差を測定します。
主に次の目的で使用されます:
真のクラスラベルを予測分布で説明できるかを評価する。
予測が正しいか、どの程度かを測るコスト関数として。
交差エントロピーの用途
二値分類タスク
交差エントロピーは「バイナリ交差エントロピー(Binary Cross-Entropy)」として使われます。
例: スパムメール検出や疾患予測モデル。
多クラス分類タスク
ソフトマックス層と組み合わせるとよく用いられ、各クラスに属する確率を出力する。
例: 画像分類(犬/猫/鳥)。
交差エントロピーの性質
交差エントロピーは、予測確率が真のラベルに近ければ小さくなる性質があります:
正しいクラスの予測確率が高い ⇒ log(高い値)\log(\text{高い値})log(高い値) は小さい負の値 ⇒ 損失が小さくなる。
間違ったクラスを予測する ⇒ log(低い値)\log(\text{低い値})log(低い値) は大きな負の値 ⇒ 損失が大きくなる。
なぜ交差エントロピーを使うのか?
出力が確率分布(Softmax や Sigmoid 関数などを使用)を前提とするタスクで有効。
損失が連続的で滑らかに変化し、勾配降下法に適している。
理論的には、情報エントロピーに基づいており、情報論の観点での正しさを持つ。
距離学習と深層距離学習
回帰問題、分類問題の枠組みに当てはまらないケースを入力、出力データを工夫したり、誤差関数を工夫することで解決。
距離学習(Metric Learning)と深層距離学習(Deep Metric Learning)は、データ間の距離や類似性を学習するための手法です。これらの手法は、特に画像認識や顔認証、推薦システムなどの分野で広く利用されています。
距離学習 (Metric Learning)
データの類似性や相違点を測るための距離を自動で学ぶ手法です。
距離学習の目的は、同じクラスに属するデータポイント間の距離を小さくし、異なるクラスに属するデータポイント間の距離を大きくすることです。これにより、データを効果的に分離するための特徴空間を構築します。
深層距離学習 (Deep Metric Learning)
深層距離学習は、深層学習技術を用いて距離学習を行う手法です。具体的には、ニューラルネットワークを使用してデータを埋め込み空間に変換し、同じクラスのデータが近く、異なるクラスのデータが遠くなるように学習します。
埋め込み空間の生成: データポイントを特徴ベクトルに変換し、類似性を反映した空間を構築します.
損失関数の設計: 深層距離学習では、Contrastive LossやCircle Lossなどの損失関数を使用して、データ間の距離を最適化します。これにより、同じクラスのデータポイントが近くに配置され、異なるクラスのデータポイントが遠くに配置されるようにします.
アプリケーション: 深層距離学習は、顔認識、異常検知、クラスタリングなど、さまざまなタスクに応用されています。特に、少ないサンプル数のクラスや未知のクラスに対しても高い性能を発揮することができます.
Siamese Network (サイアミーズネットワーク)
深層距離学習。同じ構造を持つ2つのネットワークを使用し、互いにデータを比較するニューラルネットワークモデルです。
Triplet Network (トリプレットネットワーク)
深層距離学習。3つのデータポイント(アンカー、ポジティブ、ネガティブ)を使って距離を学習するモデルです。
Contrastive Loss (コントラスト損失)
深層距離学習に使う誤差関数。
ペアとなるデータ間の距離を最小化し、非ペアのデータ間の距離を最大化することを目指す損失関数です。
Triplet Loss (トリプレット損失)
深層距離学習に使う誤差関数。
アンカーとポジティブの距離を最小化し、アンカーとネガティブの距離を最大化する損失関数です。
生成モデルにおける誤差
生成モデル(Generative Model)の誤差は、モデルが期待通りの出力を生成する能力を評価する重要な指標です。(G検定 6−5 30. データ生成)
生成問題 (Generative Problem)
新しいデータを生成することを目的とした問題で、画像生成などで応用されます。
生成モデル (Generative Model)
入力データを学習して新しいデータを生成するモデルです。その目的は、データの確率分布を学習して、与えられたデータと同様の特徴を持つ新たなデータを作成すること
生成モデルにおける主な誤差の種類とその原因
(1) 再構成誤差(Reconstruction Error)
概要: 主にオートエンコーダなどの生成モデルで評価される。入力データを再現する際の生成結果との違いを表す。
原因: 学習が不十分、モデルが入力データのパターンを正しく捉えられていない場合に発生。
例: 入力画像をノイズレスに再現できていない。
(2) 分布間距離(Divergence Metrics)
概要: モデルが生成するデータ分布と、元のデータ分布の違いを測定する。
代表的な距離計算:
カルバック・ライブラー情報量Kullback-Leibler(KL)ダイバージェンス
イェンゼン・シャノン情報量Jensen-Shannon(JS)ダイバージェンス
Wasserstein距離(Earth Mover's Distance, EMD)
原因: モデルがトレーニングデータ分布を適切に学習できていない。
(3) ノイズやアーチファクト
概要: GAN(生成対向ネットワーク)などで見られる問題で、生成されたデータに不自然なノイズやアーティファクトが含まれる。
原因: ジッターや訓練時の不安定性、過学習による影響。
(4) サンプル品質と多様性のトレードオフ
概要: 高品質なサンプルを生成する場合、多様性が失われることがある。
原因: モデルがモード崩壊(Mode Collapse, 一部のパターンに偏る)を起こしている。
(5) 適合誤差と一般化誤差
概要: トレーニングデータへの過度な適応(過学習)によるズレ。
原因: データセットが偏っている、正則化が不足している。
深層生成モデル (Deep Generative Model)
ディープラーニングを用いてデータから生成プロセスを学び、新しいデータを生成するモデルです。
変分オートエンコーダ (Variational Autoencoder, VAE)
データの潜在特徴を学習し、新しいサンプルを生成するためにオートエンコーダを変分推論で強化したモデルです。
カルバック・ライブラー情報量をベースとした誤差関数が最適計算に使われます。
目的関数
目的関数 (Objective Function)
モデルが最適化しようとする目標を定義する関数で、特にその値を最低(または最大)にすることを目指します。
