倍になるのはいつか

3/30の443名から4/4には891名へ。891/443=約2.01。
つまり東京は今(2020/4/4)、5日間で2倍のペースで累計感染者数が増加している。
【2020/4/17追記】4/17現在、東京は10日間で2倍程度のペースになっている。以下、文中に最新版グラフを追記。
【2020/5/17追記】5/17現在、東京は218日間で2倍程度のペースになっている。以下、文中に最新版グラフを追記。
【2020/7/11追記】「第2波」の感染状況を把握するには別の見方が必要になってきたようだ。ぜひ続編「増えているか減っているか」もお読みいただければ幸いである。

ウイルス感染はその仕組みからして「指数関数的に」拡大していくことは避けられない。「指数関数的に」拡大するということは、その拡大ペースを知るためには「何日間で何人増えたか？」ではなく「何日間で何倍になったか？」を把握する必要があることを意味する。（仮に毎日1.1倍になるペースだとしたら、今10人なら次の日新たに1人、今100人なら次の日新たに10人、今10万人なら次の日新たに1万人が感染することになる。ウイルスは母数が何人かはお構いなく、前日x倍率で感染を広げていくのだ。）そんな時に状況を把握するために使われるのが、今回新型コロナウイルスのグラフでもよく登場する「対数グラフ」というものだ。

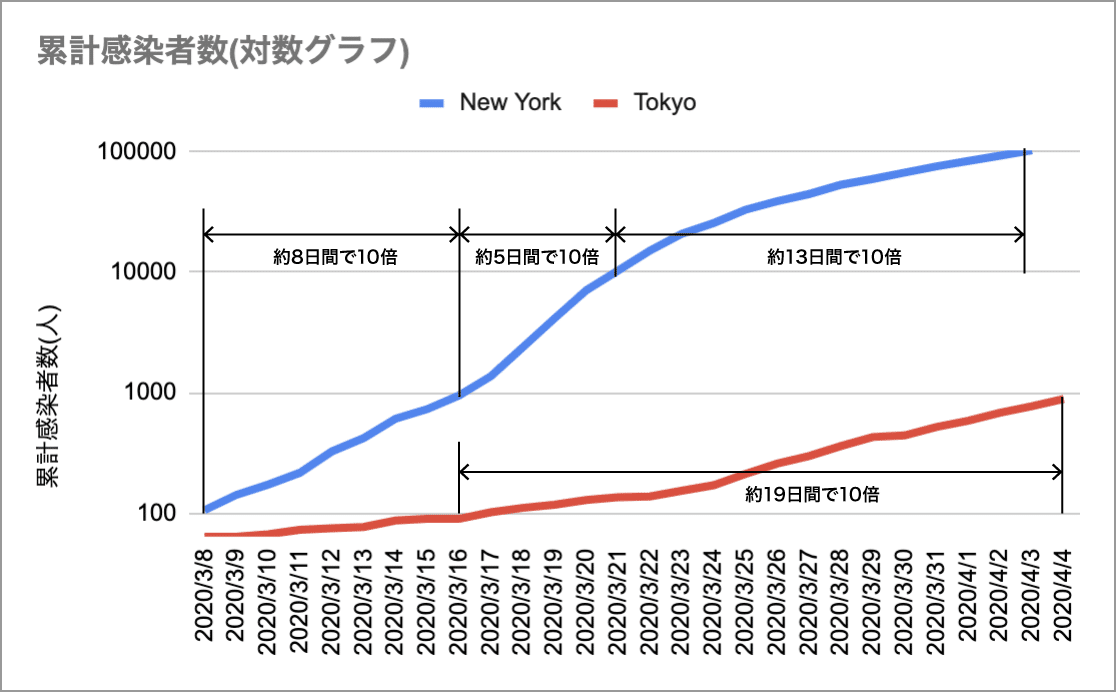
以下は、2020/3/8から2020/4/4までの東京都とニューヨーク州の累計感染者数のグラフである。（なお、東京都のデータは東京都 新型コロナウイルス陽性患者発表詳細から、ニューヨーク州のデータはNY Times Coronavirus (Covid-19) Data in the United States から取得している。）

まずは、通常のグラフ。

下に張り付いているように見える赤い線が東京都のデータであり、比較するのが難しい。これを対数グラフにしてみるとどうなるか。

縦軸の目盛りを見るとわかる通り、100人から1000人に、1000人から10000人にと、感染者数が10倍になるのに何日間かかっているかがわかりやすくなる。実際に直近のデータで見てみると、ニューヨークは10倍（1万人から10万人）になるのに約13日間、東京は10倍（100人から1000人）になるのに約19日間かかっていることがわかる。

しかし、ここで直近数日間の動きをもう少しよく見てみると、ニューヨークは傾きがもう少しなだらかになってきているし、逆に東京はわずかながら傾きが急になっているように見える。試しに直近３日間の傾向を元に対数グラフ上に直線を引いてみると以下のようになる。

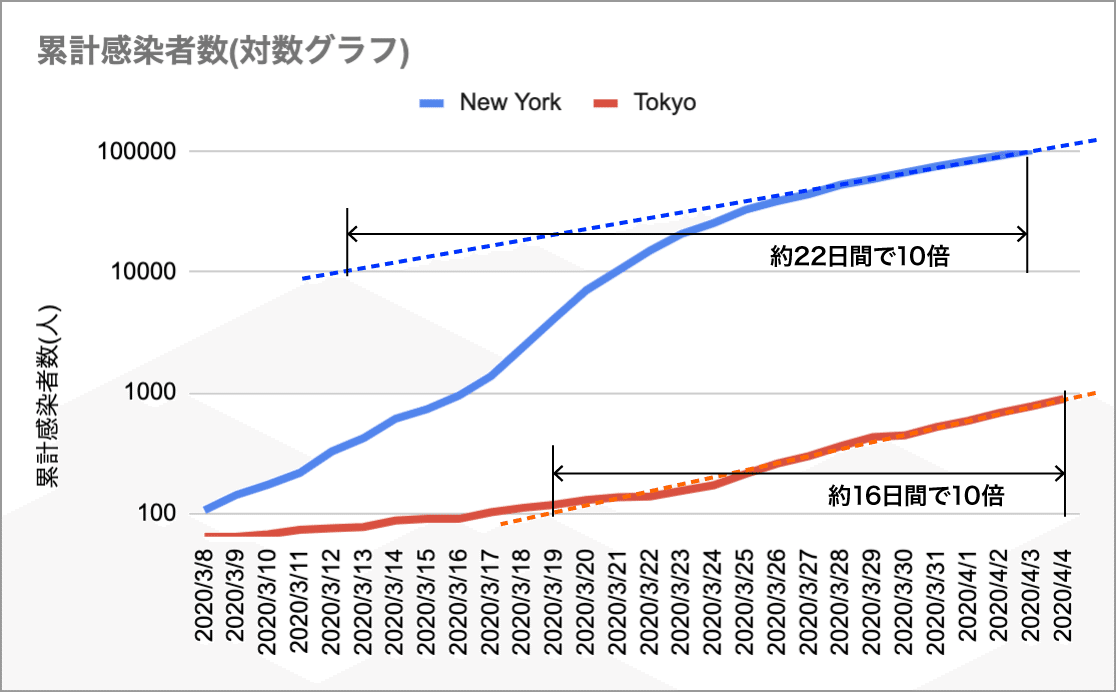
直近３日間の傾向をみると、どうやらニューヨークは約22日間で10倍くらいのペースになっているのに対して、東京は約16日間で10倍くらいのペースになっているようだ。ニューヨークはペースが落ち、東京はペースが上がっている。東京はやはり要注意だ。

対数グラフの傾き

このように、「何日間で何倍になるペースか？」は、対数グラフの傾きから読み取ることができる。しかし、毎日グラフに直線をあてがって傾きを測るのは面倒である。そこで、上のデータを元に「10倍になるのに何日間かかるペースか」を数式で求めたいのだが、それは以下の式で求めることができる。（参考：片対数グラフ，両対数グラフの傾きの意味）

高校の数学で出てきたlogだ。計算はコンピュータがやってくれるので、何はともあれ実際のデータを入れてみることにしよう。検査や集計のタイムラグなどを考え、直近3日間のデータを元に計算してみると以下のようになる。

お、先ほどの対数グラフに直線を当てがった値とほぼ一致している。どうやら式は合っていそうだ。さて、実はこのlogというのはlog10（常用対数）のことである。そこで、今度はこれをもう少し一般化して、n倍になるのにかかる日数を求める式にしてみよう。

10がnになっただけである。では、n=2として、先ほどと同じデータを入れてみよう。

直近３日間のデータを元に計算すると、ニューヨークは約7日で2倍に、東京は約5日で2倍になるペースで感染が拡大していることがわかる。ようやく冒頭の結論に到達した。

ペースは上がっているか？

さらに、こうして数式化ができると、そのペース自体がどう推移しているかも計算することができるようになる。

ニューヨークは、3/11時点（累計感染者数217名）から2週間、ほぼ「2日で倍」という猛烈なペースで感染が拡大したことがわかる。ただ、ここ1週間はペースダウンしてきている。一方の東京は「10日で倍」くらいのペースを保ってきたのだが、ここにきて「5日で倍」のペースに上がってきている。（直近は横ばい傾向にも見えるものの決して油断は禁物だろう。）

【2020/4/17追記】4/17現在、東京は再び「10日で倍」のペースを取り戻している。おそらくこれから数字に現れてくるはずの緊急事態宣言後の行動変容の効果でさらにペースが落ちていくことを期待したい。

【2020/5/17追記】5/17現在、東京の累計感染者数の倍加日数（2倍になるのにかかる日数）は218日までペースが落ちている。（直近7日間の増加率を元に計算。）そろそろこのグラフも役目を終え、このまま収束へ向かうことを期待したいところである。

直感と数学

「何日間で何人増えたか？」ではなく「何日間で何倍になったか？」という指数関数的な増加を、日々報告される感染者数だけで直感的に感じることはとても難しい。（しかも実際に医療の現場のキャパシティとして問題になるのはあくまで何人の方である。）しかし、一見直感的でなさそうな数学を使うことで、このような直感しづらい事象を、「〇〇日で倍」といったように少し直感に近づけることもできる。「数学は役に立つ」のである。（ちなみに、倍になるのにかかる時間を「倍加時間」という。また「対数」に興味を持った方がいたら、こちらのページの解説などがわかりやすいかもしれない。）

最後に

この記事で示しているのは、あくまで冒頭に示した累計感染者数のオープンデータのみを使った単純な計算結果であり、予測ではないことはご注意いただきたい。実際には、そもそも感染者数は検査数にも左右されるので、実態との乖離がある可能性がある。また、当然それぞれの都市の人口以上に無限に（ドラえもんのバイバインのように）増え続けるわけではないし、「密閉・密集・密接」を避ける行動など、わたしたちの日々の行動変容が今後の拡大ペースを抑えることにもつながる。（行動変容は1〜2週間ほど遅れてデータに現れてくるはずだ。）今はやはり、人との接触を出来るだけ避ける行動が重要であることは間違いない。

「欧米に近い外出制限を」　西浦博教授が感染者試算

なお、「指数関数的増加」に関連する話題としては、ロジスティック関数というものを使って人口の上限を考慮し、増加率がいずれは低下していくことを示した、WIREDの『指数関数的に拡散する新型コロナウイルスの対策として、「カーヴの平坦化」こそ重要である数学的な根拠』という記事も参考になるだろう。

また、この記事では、あくまで「何日で倍になるか」を計算しているが、もちろん同じ直近3日間のデータから「1日で何倍になるか（何%増加するか）」という計算もできる。（そちらの方がもっと計算は単純だ。）4/4時点で、東京はおよそ前日比15%で推移している計算になる。