
増えているか減っているか
一旦収束に向かったかに思えた日本国内の感染状況だが、連日報道されているように再び感染が「第2波」として拡大しつつある。4月はじめ、指数関数的に拡大するウイルス感染を「倍になるのはいつか」という見方で把握することについて書いたが、第2波についてはそれだけでは状況を正しく把握することはできなそうである。状況はよくなっているのか悪くなっているのか?感染は拡大しているのか収束しているのか?今回は第2波を前提に「コロナで数学」第2弾として改めて考えてみようと思う。
何の増減が大事か?
増えている減っているという話をする前に、そもそも「何が」増えているもしくは減っていることが大事なのか、Whatについてまず改めて確認したい。
メディアでは連日「新規感染者数」ばかりがクローズアップされるが、そもそも、本当に注目すべき数字は「新規感染者数」だけでいいのだろうか。経済を止め、日常生活を制限することが妥当かどうかは、それだけでなく、感染したら症状はどれくらい重く辛いのか、死に至る危険はどれくらいあるのか、治るとしてどれくらい長引くのか、後遺症はどれくらい残るのか、といった、そのインパクトの大きさも同時に見る必要があるだろう。そのためには、新規感染者数だけでなく、入院者数、重症者数、死亡者数などの数字が重要になる。
では、それらのデータは実際どうなっているだろうか。まずは、少しグラフを巻き戻して第1波(4月)の状況を振り返ってみよう。

日々のばらつきや曜日の影響をならした7日間の移動平均線を見てみると、4月の時点では、新規感染者数と入院者数、重症者数のグラフはあまりタイムラグもなく同じ傾向を示していることがわかる。(死亡者数は最後に訪れる結果なので遅れて傾向が現れている。ただし4/13から集計方法が変わっている点は注意。)
これは、高熱が何日も続くなど、明らかに入院治療が必要そうな人に絞って検査を行なっていたから、ということが理由の一つとして考えられるだろう。その方針が適切だったか議論はあるにせよ、いずれにしてもこの4月の時点では「新規感染者数」に注目していれば、入院者数、重症者数の傾向もつかめ、医療体制は大丈夫か、ひいては感染を防ぐ行動制限は妥当か、といった本当に知りたいことが把握できたのである。
では、同じグラフで現在(2020/7/11)の状況はどうなっているだろうか。

6月後半から新規感染者数は増え始めたが、入院者数は6月はまだ減少傾向か横ばいである。7月に入って入院者数はやや増加に転じているが、重症者数はいまだ減少傾向である。これは、4月に比べて対象範囲を広げて検査を行なっていることや、いまだ決定的なワクチンや治療薬はないとしても、医療の現場の体制や対処法が確立されてきたことなどが理由として考えられるだろう。これもまたいろいろな見立てがあるだろうが、いずれにしても4月のように「新規感染者数」だけを見ていても全体像は把握しづらくなっているとは言えそうだ。
第2波はどうやら第1波とは状況が違うらしい。つまり、1日の新規感染者数が同じでも第1波と第2波では意味が違うのである。このまま感染者数は増えても重症化する人は増えないのか、タイムラグがあるだけで再び重症化する人も増え医療体制が逼迫してしまうのか、第2波がどんな様相を見せるのかはまだまだよくわからないというのが現状ではないだろうか。
ちなみに、感染者数は増えても死亡者数はそれほど増えていないのは日本国内だけでなく、世界的な傾向でもあるようだ。
当然、楽観論も悲観論も様々ある。感染者は増えても重症者が増えないのであれば、風邪やインフルエンザのようなものとして、新規感染者数をいちいち気にする必要はなくなるだろう。
とはいえ、である。本当にそうなったらいいなと思うのだが、日本国内の直近の入院者数や重症者数の傾向を移動平均線で注意深く見てみると、緩やかながらそれぞれ増加傾向にはあるし、世界的にも例えばアメリカでは感染者数だけでなく死亡者数も再び増加に転じている。
個人的には楽観的な希望も持っているものの、同時に悲観的なシナリオとして今後再び入院者数や重症者数が増えてしまう可能性を考えると、やはり新規感染者数という数字に意味がないとは思えず、今後の状況の変化の兆しを一早く知ることができる指標として、引き続き注目すべき指標ではないかと思うのである。
どんなペースで増えているか減っているか?
ここまで、「新規感染者数」というWhatの意味を改めて考えてきたが、次に、それが今どんなペースで増えているのか、Howについても改めて考えてみたい。
前回の記事では、「何日で倍になるか?」という倍加時間と呼ばれる指標を使って、感染拡大のペースを把握することを考えたが、この時に使っていた数字はあくまで「累計の」感染者数が何日で倍になるか?であった。これは、流行の最初の波を把握するにはよいが、第1波で感染したほとんどの人はすでに治っていて他の人には感染させないわけで、一旦収束したあとの次の波を考えるのに、第1波を含めた累計が倍になるペースを考えるのはもはや適切ではない。
そこで出てくるのが、よく耳にするようになってきた再生産数R、すなわち「1人が何人にうつすか」という指標だ。これがわかれば、今までの累計に関わらず、Rが1より小さければ感染者は減り、Rが1より大きければ感染者は増えるということがわかる。(ちなみに、人口が減るか増えるかを把握するための出生率も同じような考え方に基づいたものである。)
しかし、ここで話をややこしくしているのが、再生産数には、基本再生産数R0(=誰も免疫を持っていない状態を想定した素の再生産数)と実効再生産数Rt(=現状に即した実際の再生産数)の2種類があることだ。データからわかるのは実効再生産数Rtだが、それはあくまで、
Rtが1より小さい=今のままなら感染者は減る
Rtが1より大きい=今のままなら感染者は増える
ということであり、この「今のままなら」というところが重要だ。
これを混同して「Rtが1を下回ったからほっといても減り続ける。(だから1を下回った後の自粛は必要ない)」とは言い切れない。「Rtが1を下回ったから今のままなら減り続ける。(自粛をやめたらどうなるかわからない)」のである。もしロックダウンや自粛が必要ないのなら、解除後もRtは1より小さいままであるはずで、そうなることを期待したが、やはり解除したら1を超え、感染者数は再び増え始めているのが現実である。
再生産数はどうすればわかるか?
さて、では再生産数はどうすれば求めることができるだろうか。まず、基本再生産数R0については、当初は2.5程度と言われたり、いやもっと小さいのではと言われたりしているが、何らかの対策や行動制限が行われている今の状況では正確にはわからない。
では、実効再生産数Rtの方はというと、これもいろんな定義や計算式があり、さらに話をややこしくしているが、基本的な考え方についてはこの動画がわかりやすく簡潔にまとまっていると思う。
【実効再生産数の考え方】
— 新型コロナクラスター対策専門家 (@ClusterJapan) May 29, 2020
北海道大学 小林鉄郎 による再生産数についての解説第2弾です。
今回は実効再生産数の考え方について解説します。#新型コロナクラスター対策ゼミ pic.twitter.com/vOZnscPuvK
動画にもあるように、もし「誰が誰にうつしたか」が正確にわかれば、単純にRtはうつされた人数/うつした人数、で求めることができる。3人が次に6人にうつしたことがわかればRt=6/3=2というわけだ。しかし、現実には「誰が誰にうつしたか」をすべて把握するのは不可能である。しかも、そもそも把握できているデータ(検査数)が少ない、集計にタイムラグ(感染>発症>診断>報告で約2週間)がある、データが不完全(報告日しかわからないなど)などといった状況が推計をいっそう難しくし、その結果いろいろな定義や計算モデルが存在することにもなっている。上の動画で紹介されているのはいわゆる西浦モデルとも言われているものだが、最後の残り数秒のところで唐突にめちゃくちゃ難しそうな数式が出てきて面食らってしまう。

(「実効再生産数とその周辺」より)
数学が得意な人は、解説を見ながらじっくり自分の手で計算してみたり、プログラミングが得意な人はGitHubのソースを見ながらJupyter notebookでプログラムを動かしてみると、なるほどと理解できるかもしれない。ただ、私自身も興味はあるもののなかなかそんな時間は取れていない。
同じようなコンセプトでもっと簡単なモデルはないのだろうか?今後の対策に活かしていくには、より簡易的でリアルタイム性を重視したモデルでも十分意味があるのではないだろうか。実は、上記の一見めちゃくちゃ難しそうな資料の最後に、次のような指標が対案として紹介されている。それは「直近7日間の新規感染者数が、その前7日間の新規感染者数より多いか?」というものだ。なんだか拍子抜けするほど簡単だが、これは1931年にスペイン風邪を分析したStallybrassによって提案されたRatio of dispersibilityという考え方に基づくものであるらしい。


(「実効再生産数とその周辺」より)
実際に、直近のデータで見てみると、計算するまでもなく直近7日間(7/3〜7/9)の新規感染者数は、その前7日間(6/26〜7/2)の新規感染者数より多いことがわかる。
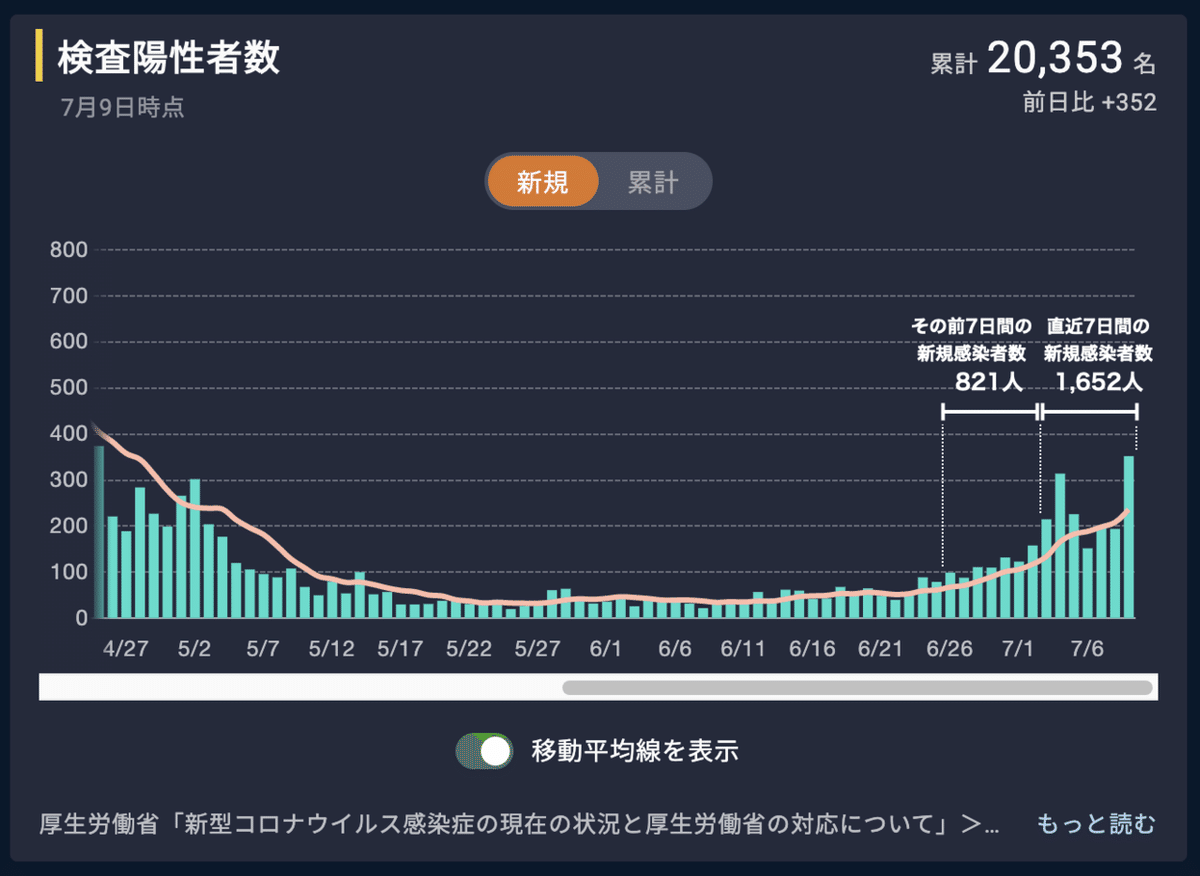
(「新型コロナウイルス国内感染の状況」に加筆)
明らかに増えていることはわかったが、具体的にどのくらいのペースで増えているのだろうか?まずはRatio of dispersibilityを求めてみよう。計算は簡単で「直近7日間の新規感染者数/その前7日間の新規感染者数=1652/821=2.01」となる。先週の感染者に対して今週はその2倍の感染者が新たに生まれている。もし仮に感染者の世代交代のペースがちょうど1週間だとすると、この2.01がそのまま実効再生産数Rtということになる。

どのくらいのペースで増えているか減っているかを知りたいだけなら、このRatio of dispersibilityで十分な気もするのだが、一応これを実効再生産数Rtに換算することを考えてみよう。これまでの分析から実際の感染者の世代交代のペース(平均世代時間)は約5日間とのことである。そこで、2.01を「5/7乗」すると、これが、東洋経済オンライン「新型コロナウイルス国内感染の状況」のグラフにある実効再生産数Rtの値になる。

(「新型コロナウイルス国内感染の状況」に加筆)
ちなみに、なぜ単純に2.01に5/7をかけるのではなく「5/7乗」する必要があるかというと、7日間で2.01倍なので、1日あたり何倍かを考えるためには「7回繰り返すと2.01になる倍率」を求める必要があるのだ。具体的に計算してみると少しわかりやすいかもしれない。結果は確かに上のグラフと同じ1.65になる。

余談だが、1930年にさきほどのRatio of dispersibilityを提案したStallybrassもこれを勘違いしていたらしく、90年前の疫学の教科書の間違いに気づいた西浦氏は思わずビックリマークを書いてしまったらしい。

(「実効再生産数とその周辺」より)
ここまでの計算をまとめて書いてみると、簡易的な実効再生産数Rtを求める式は次のようなものになる。

なお、このあたりの話も含めて、以下の動画で西浦氏による解説を見ることができる。如何せん全体的に難しい話が多いのだが、今回紹介した話は59分あたりから10分くらいなので、興味をもたれた方をぜひ見てみて欲しい。
感覚と数学をつなぐ言葉とイメージ
さて、ここまで読んでいただいた方はどれほどいるだろうかやや不安であるが、前回に続いて「コロナで数学」第2弾として、今回は第1波と第2波の違いや実効再生産数について取り上げてみた。最初に書いたように、これからは新規感染者数だけでなく、入院者数や重症者数も注目すべきだし、ウイルスによる体への影響と行動制限による社会や経済への影響のバランスも考えなければならない。
また、結論から言えば、少なくとも今回紹介した簡易的な実効再生産数は、1より大きい=今週は先週より新規感染者数が増えているよね、という、言ってみればただそれだけの、特に今のように明らかに増えている時には言われなくてもわかるようなことではある。ただ、その傾向を感覚だけではなく数学的なモデルとして計算することで、増えているか減っているかがより確実にわかるし、その増え方のペースもわかるのである。
コロナに限らず、現実の世界で起きていることを感覚的に語ることも大事だが、数学やアルゴリズムの世界には、またそれとは違った面白さがある。文系と理系、右脳と左脳といった分け方を安易に使いたくはないが、いろいろな記事を見ていても、感覚的な話や思想的な話と、数式やプログラミング言語を使ったとても専門的な話のあいだに分断があり、それらをつなぐような言葉やイメージがすっぽりと抜けているように常々感じている。これはどちらが正しいとか優れているいうことではなく、数学やアルゴリズムを扱う側もそれで全てがわかったような気にならず、以前反証主義について紹介したように、正しさの限界についても常に謙虚でありたいし、何より数学やアルゴリズムを含めた科学やテクノロジーをブラックボックスにしてしまわない工夫がもっと必要だと思うのだ。
つくることでわかる
このような問題意識は、数年前にNHK EテレのAI特集番組で2分×12回のアニメーションで「ディープラーニング」の基本的な概念を紹介するコーナーの企画製作に関わった時にも感じていた。その時にも、ビジネス書などに一般向けとして書かれているような感覚的な説明でもなく、かといって数式やプログラムなども使わずに、ニューラルネットワークの基本からバックプロパゲーション、過学習、CNN、RNN、GAN、深層生成モデル、深層強化学習といった概念をそれぞれ2分間のアニメーションで説明することに挑戦した。(ちなみに当時はこのコーナーはウェブ上で見ることができ、よい反応もいただいたりしていたが現在は残念ながら見ることができない。)
このnoteでは「わかるとつくる」をテーマに記事を書いているが、この「コロナで数学」にせよ「2分でディープラーニング」にせよ思うことは、人に伝えるために「つくる」こと自体がなにより「わかる」につながるということだ。そして、つくってみるとまたたくさんの「わからない」も生まれる。続けられるかどうかわからないが、今後もこういった数学やアルゴリズムの世界を自分自身も学びながら、できるだけわかりやすく伝えられるようなコンテンツや記事を書いていけたらと思う。
この記事が気に入ったらサポートをしてみませんか?


