ヒューリスティックコンテスト(マラソン)、ゲームAIコンテストで使う武器まとめ
ものづくりとプログラミングとルービックキューブが大好きなにゃにゃんです。今回は競技プログラミングに関する内容です。
この記事の執筆時点ではもうすぐAHC002というヒューリスティックコンテストが開かれます。
これに向けて過去問を解いて準備をしていて、ヒューリスティックコンテストやゲームAIコンテスト(基本的にまとめて「ヒューリスティックコンテスト」と言うことにします)における様々な武器やTIPSがわかってきました。それを自分のメモも兼ねてまとめます。なお、深さ優先探索や幅優先探索など、アルゴリズムコンテストでもよく出てくるアルゴリズムについては省きました。ただでさえ記事の文字数が結構多くなってしまったので…
この記事は私が今後精進していく中で新たな発見があったら随時追記していこうと思います。
ヒューリスティックコンテストとは
ヒューリスティックコンテストは、ある問題が与えられて、それに対する解をコードで提出する、プログラミングコンテストの一種です。
普通のプログラミングコンテストは解が一意に定まる問題に挑戦することに対し、ヒューリスティックコンテストでは「この問題に対してなるべくこのような状態に近づけてください」というような問題が出ます。最適化問題などが頻繁に出ます。
ゲームAIコンテストとは
ゲームAIコンテストもプログラミングコンテストの一種ですが、その名の通りゲームAI(ゲームを自動で対戦するプログラム)を作るコンテストです。ヒューリスティックコンテストとは近いようでそんなに近いわけでもないので、この記事では分けて書くことにします。ただ、ヒューリスティックコンテストでもゲームAIの知識が使える場合もあるのでなんとも言えませんね。
大事なこと
まず、ヒューリスティックコンテストもゲームAIコンテストも、深さ優先探索と幅優先探索と以下で紹介する貪欲法さえわかっていれば十分楽しめます。ぜひ気軽に挑戦しましょう!
ヒューリスティックコンテストは、解を導くことについては簡単な場合が多いです。何も知識がない状態でも、とりあえず貪欲法や乱択を使った解法で解をつくり、それを見て改善していくことで十分楽しめます。
以下では「〇〇法のポイント」をいっぱい挙げますが、必ずしも一部または全てを実装しないと動かないものではありません。基本的な概念と実装方法さえわかれば、とりあえず動きます。そして、ほぼ必ずスコアは良くなります。
最初から凝った実装をすると私もよくバグらせます。まずは基本的な最低限の実装をして、それに追記する形でポイントを押さえていくのが良いです。
そしてヒューリスティックコンテストでとても大事なことですが、なるべく抽象的に書けるようにしましょう。プログラム内では同じような処理をたくさんすることがとても多いです。処理を細かくグループに分け、それぞれの処理を関数にしてきちんとした名前をつけるとバグが少なく、バグがあってもすぐ直せるプログラムになります。ちなみに以下で私の実際の提出リンクを貼っていますが、提出したのがヒューリスティックコンテスト始めて間もない頃だったので全く抽象的に書けていないことがあります。反面教師にしてください。
ヒューリスティックコンテストは問題の特性によって良いスコアを出せるコードが特に大きく変わります。解法選択も大きいですが、下に書く「〇〇法のポイント」は、なるべく汎用的なものを書きましたが問題によってはスコアが良くならないものもあると思います。
ヒューリスティックコンテスト(マラソン)編
ここからしばらくゲームAIではなくヒューリスティックコンテストで使うアルゴリズムについて解説します。
全体像
ここで紹介するアルゴリズムが互いにどんな関係を持っているのかを図で示します。

貪欲法は単純な手法でそれなりに良い解を1つ作る手法
ビームサーチは貪欲法の発展で、貪欲法以上の解を1つ作れる
山登り法は貪欲法などで作った初期解を洗練していく手法
焼きなまし法は山登り法の発展で、山登り法よりも局所解に落ちにくい
遺伝的アルゴリズムは解の多様性を使ってたくさんの解を同時にそれなりに良いものにするアルゴリズム
と思っていただけると良いと思います(異論受け付けます)。
なお、記事としてはこのまま記事の順番に読んでいただけると一番わかりやすいと思いますが、実際に技法を学ぶ際には、
貪欲法 -> 山登り法 -> 焼きなまし法 -> ビームサーチ -> (遺伝的アルゴリズム)
とすると、即戦力になってかつわかりやすいと思います。
遺伝的アルゴリズムはヒューリスティックコンテストでほとんど出番がない(と私は思っている)ので、カッコをつけました。ですが、遺伝的アルゴリズムと他のアルゴリズムを併用するととても良い解を導ける場合もあります。
山登り法
ヒューリスティックコンテストでかなりの場合に有効なのが焼きなまし法ですが、その簡易版とも言えるのが山登り法です。
山登り法はある初期解(ランダムに作ったものでも貪欲に作ったものでもなんでも良いです)を少しずつ変化させて、だんだんと解を洗練していく手法です。
例として、解が0から9の数字で構成された配列であるとしましょう。
解の配列が例えば
0123456789012であるとします。ここから要素を一つ選んで、例えば以下のように8番目の要素を7から0に変更します。
0123456789012
0123456089012ここでできた新たな解は、前のものとは異なります。ですが、もとの解と新たな解は「近い」と言えます。要素が1つだけ違うので、まあ大体一緒だということですね。このように、もとの解を少しだけ変えて新たな解を得ることを、「近傍を取る」などと言うこともあります。近傍の取り方は解の形式や問題の特徴によります。
さて、近傍を取ったらその近傍(新たな解)がもとの解よりも良い状態か(基本的にはスコアが良いか)を見ます。良い状態になっていたらもとの解を新たな解で置き換え、悪くなっていたら置き換えません。
山登り法は以下の実装をしています。
def scoring(state):
return stateのスコア
state = 初期状態を適当に作る
score = 初期状態のスコアを計算する
while 現在までの実行時間 < 制限時間:
new_state = 近傍を取る
new_score = scoring(new_state)
if new_scoreがscoreよりも良い:
state = new_state
score = new_score山登り法は、「今ある解のすぐ近くは点数が悪いが、もう少し遠いところにもっと良い解がある」という場合に弱いです。この弱点を克服したのが焼きなまし法です。
以下は山登り法における私が思うポイントです。
近傍のスコア計算は差分を取って高速に
山登り法はwhileのループ回数が多ければ多いほど良いです。そして多くの場合、スピードのボトルネックは近傍のスコア計算にあります。スコア計算について、例えばスコアが部分スコアの和で表されているとしたら、部分スコアを全て配列に保存しておいて、
new_score = score - 部分スコアの変更した部分 + 新たに計算した変更部分の部分スコアと高速に書くことができます。
状態遷移を高速に
状態遷移も高速にできる場合が多いです。例えば配列の要素を一つ変更するだけなら、近傍を完全な形で保持しておく必要すらない場合があります。例えば、解が配列であるとして、近傍として配列のidx番目をnumに置き換えるなら、idxとnumの情報だけ変数に格納しておいて、解を更新する時に配列のidx番目をnumに変更すれば良いです。
時間管理は毎回やらなくても良い
経過時間は毎ループ確認しなくても問題ない場合が多いです。私の場合、適当な変数としてtを使って、毎ループtをインクリメントし、tが一定以上になったらt=0として経過時間を更新します。このとき、ループ回数が2^Nごとに時間を更新するとすれば、ビット演算を用いて高速にtが一定以上かをチェックできます。
また、毎ループやる必要がないが、一定期間ごとに更新したい値が他にもあれば、時間の更新と同時に行ってしまいます。
状態を変化させたあとに貪欲法をかけたものを近傍にしても良い
少しの状態変化でほぼ必ずスコアが悪化する場合は、後述の貪欲法を使って近傍を作っても良いです。「巨大近傍」という方法に近い気がします。
以上のポイントをまとめて詳しく疑似コード(Pythonに似ています)を書くとこうなります。
def scoring_part(idx, num):
部分スコアを計算する
return 部分スコア
state = [3, 1, 4, 1, 5, ..., 9, 2, 6] # 状態
part_score = [scoring_part(idx, state[idx]) for idx in range(len(state))] # 部分スコアを全部保管した配列
score = sum(part_score) # スコアは部分スコアの和とする
t = 0
while 経過時間 < 制限時間:
num = randint(0, len(state) - 1) # 変更後の数をランダムに決める
idx = randint(0, 9) # 変更するインデックスをランダムに決める
# new_stateを必ずしも作る必要はない
score_plus = scoring_part(idx, num) # idx番目の部分スコアを計算する。
new_score = score - part_score[idx] + score_plus # 近傍のスコアを少ない計算量で求める
if new_scoreがscoreよりも良い:
score = new_score
state[idx] = num # 状態更新も一箇所の変更のみならこれで良い
part_score[idx] = score_plus # 部分スコアの更新も忘れずに
t++
if tが一定以上:
t = 0
経過時間を計測
# その他頻繁に行う必要のない処理があれば一緒にやる
焼きなまし法
焼きなまし法はヒューリスティックコンテストで出てくる定番中の定番のアルゴリズムだと思います。仕組みは山登り法に酷似していますが、山登り法では点数が良くなった場合のみ変化を受け入れますが、焼きなまし法では点数が低くなっても、ある確率で受け入れます。
点数が低くなっても変化を受け入れる可能性があるというのは、山登り法の欠点である「今ある解の周辺の点数は少し低いが、もう少し遠くの解は今よりもスコアが良い」という場合に、少し遠いところにあるより良い解に確率的にたどり着けることを意味します。
焼きなまし法では温度関数と確率関数が新たに出てきます。詳しい理論は私も知らないのですが、とりあえずうまくいきやすいメジャーな方法を書きます。
焼きなまし法は以下の疑似コードで表せます。
def temperature(経過時間, 制限時間):# 温度関数
return 温度
def prob(score, new_score, 経過時間, 制限時間): # 確率関数
return 変化を受け入れる確率
state = 初期状態を作る
score = 初期状態のスコアを計算する
while 現在までの実行時間 < 制限時間:
new_state = 近傍を取る
new_score = 近傍のスコアを計算する
if prob(score, new_score, 経過時間, 制限時間) > random():
state = new_state
score = new_score主要な処理は山登り法と同様ですが、変化を受け入れるかを決めるif文が変わりました。
温度関数と確率関数は具体的に、例えば点数を最大化する場合には以下のように書きます。
start_temp = 20
end_temp = 5
def temperature(経過時間, 制限時間):
x = 経過時間 / 制限時間
return pow(start_temp, 1 - x) * pow(end_temp, x)
def prob(score, new_score, 経過時間, 制限時間):
d = new_score - score
if d >= 0:
return 1
return exp(d / temperature(経過時間, 制限時間))温度関数は以下のように書くこともよくあります。
def temperature(経過時間, 制限時間):
x = 経過時間 / 制限時間
return start_temp + (end_temp - start_temp) * x温度関数は他にも様々な関数が考えられますが、基本的にはstart_tempからend_tempに徐々に移動する単調減少の関数で表されます。
そして、確率関数は、点数が上がっていれば必ず1を返し、点数が下がっていれば、
・まだ時間があまり経過していなければ、exp(悪化量(負) / 大きな値(正))を返す
・焼きなまし終盤では、exp(悪化量(負) / 小さな値(正))を返す
という挙動をします。ここで、大きな値や小さな値と書いたのは温度関数が返す値で、単に「温度」とも呼ばれます。
確率関数と変化を受け入れるか決定するif文の挙動を言葉で説明すると、序盤は多少大きな点数の悪化もそこそこの確率で受け入れ、終盤は小さな点数の悪化も滅多に受け入れないという挙動をします。温度が高い序盤はより良い解を探して冒険し、温度が低い終盤は今ある解を洗練することに力を注ぎます。
焼きなまし法を使うことで、山登り法よりもスコアが上がることがあります。
焼きなまし法は山登り法の発展なので、ループ回数が命なことに変わりはありません。焼きなまし法のポイントは山登り法のポイントに加えて以下です。
最初/最後の温度はだいたい序盤/終盤のスコア変動の上限くらい
こう書いたのですが、この考えに固執しすぎず、スコア変動の上限くらいの値を適当に入れてみて統計的に点数が上がる値を見つけましょう。ただ、ものすごく時間が溶けるのでコンテスト終盤でやると良いです。
温度と確率は事前計算すると速くなることがある
温度と確率はときに10^7回から10^8回計算することがあります。これだけの回数毎回関数を呼んで計算するのはなんとなく無駄な気がします。事前計算して配列に値を格納しておいて、その値を呼び出すと多くの場合で高速になります。焼きなまし全体が10倍速になった場合もありました。所詮時間経過と確率を返すので、精度はそこまで高くなくても良いです。概ね時間経過は10^4要素、確率は10^5から10^6要素あれば十分だと思います。
最高スコアの状態を保存しておく
焼きなまし法でも時々、あまり良くない状態にハマって抜け出せなくなることがあります。最高スコアを叩き出したあとしばらく周辺を探索してみたもののスコアは上がらず、最高スコアの解からどんどん離れていってしまう場合があります。そんなときはある時刻におけるそれまでの最高スコアの解を常に保持しておき、一定時間点数が上がらなかったら強制的に最高スコアの状態に戻すようにすると良い場合があります。やりすぎると狭い範囲しか探索できなくなるので、ほどほどにすると良いと思います。
同スコアが多く存在する問題では、同じスコアの状態を複数保存しておく
スコアが整数で刻みが大きい場合などは、同点の解がたくさんできることがあります。そんなとき、一つの解に固執して探索すると局所解にハマってしまう場合があります。このような場合には同じスコアの状態を見つかった都度保存しておいて、各状態について一定時間ごとに強制的に見ていくことを繰り返すと局所解にハマりにくくなると思います。これは「多点スタート」と呼ばれる焼きなましの技法に近くて、多点スタートを様々な時刻に行うイメージです。
でもこのような場合はスコアをオリジナルの評価関数に置き換えて刻み幅を小さくした方が良いかもしれません。
初期解によってスコアが大きく変わる場合がある
山登り法でも焼きなまし法でも初期解を作ってそれを改善します。山登り法では初期解から単調にスコアが良くなるところを探しますが、焼きなましはそうではなく、比較的広い解空間を探索できます。ですが、温度や制限時間によっては解空間のあまり広くない範囲を探索することになることがあり、その場合は初期解によってスコアが大きく変わる場合があります。多点スタートで乗り切る方法もあると思いますが、高速化や温度調整を少し頑張り、上に書いた最高点保持などもあわせて使うとうまくいくことが多い気がします。
最後に焼きなまし法が活躍した問題と私の提出を貼ります。
本番25位でした。解説記事はこちらです
貪欲法
貪欲法は前述の山登り法や焼きなまし法で使う初期解を作るのに役に立つことが多いほか、とりあえずそのまま提出して正の得点を得るのにもよく使えます。
多くの場合において、解を作る場合には少しずつ解を構成していくことが可能です。例えば配列を要素0番目から順番に埋めていくなどです。
例として解のidx番目に0から9までのどれかから数を選んで入れることを考えます。このとき、貪欲法では基本的に、全てのパターンについてスコアを計算し、一番その時点でのスコアが良かったものを採用します。時間的な制約が厳しかったり、考えられる手が多すぎたりしたら私は乱択を使うこともあります。基本的な実装を擬似コードで示します。
def scoring(idx, num):
return state配列のidx番目にnumを代入したときのスコア
state = []
for idx in range(N):
best_score = 悪いスコア # 考えうる最悪スコアよりも悪いスコアで初期化する
best_num = -1
for num in 考えうる手: # 考えうる手を全部試してみる。多すぎたら乱択を使うこともある
score = scoring(idx, num) # その時点でのスコア
if scoreがbest_scoreより良い:
best_score = score
best_num = num
state.append(best_num)貪欲法は常に真に最適な解を返すとは全く限りません。ヒューリスティックコンテストではなくてアルゴリズムのコンテストでも、よく「未証明のgreedy(貪欲)は危険です」と言いますね。でもそれなりに良い解を出してくれるので、山登り法や焼きなまし法の初期解によく使えます。
ポイントを以下にまとめます。
未完成の解ではスコアが計算できない場合は適当に乱択で残りを埋めても良い
必ずしも解を構成している途中で点数が計算できるとは限りません。そのような場合は埋めていない残りの解を乱択で埋めて、全部埋めた場合のスコアを用いたりします。貪欲法だけで最終的な解を作ることは少ないので、貪欲法で作る解はそれなりに良ければ良いです。
高速化にそこまで恩恵はないが、しておくと良い場合が多い
試行回数が命である山登り法や焼きなまし法と違って、貪欲法はそこまで高速化しなくても問題はありません。ただ、基本的には貪欲法が終わったら他の時間をいっぱい使うアルゴリズムで解を洗練するので、貪欲法が高速であればあるほど多少良い場合が多いです。高速化には前述の通り点数を差分で計算することができることが多いです。また、これも上と同じことを言いますが、様々なパターンを試す中でそれぞれ配列を生成してスコア計算すると遅いので、配列をいちいち作らずにスコア計算できると良いです。
最後に貪欲法が活躍した問題と私の提出を貼っておきます。
この問題で私は記事執筆時点の世界最高点を持っています。ちなみに乱択の貪欲法のみを使っています。
解説記事はこちら
ビームサーチ
ビームサーチは前述の山登り法や焼きなまし法とは全く違うアルゴリズムで、貪欲法に近いです。
貪欲法では解を少しずつ埋めていく場合、一番スコアが良い手を採用していましたが、ビームサーチではスコアが良い上位複数個の解を使います。イメージ図は以下です。採用する解の個数は2個で、×を書いた状態は上位2つの状態に入らなかったので探索を打ち切った(枝刈りした)ことを示します。
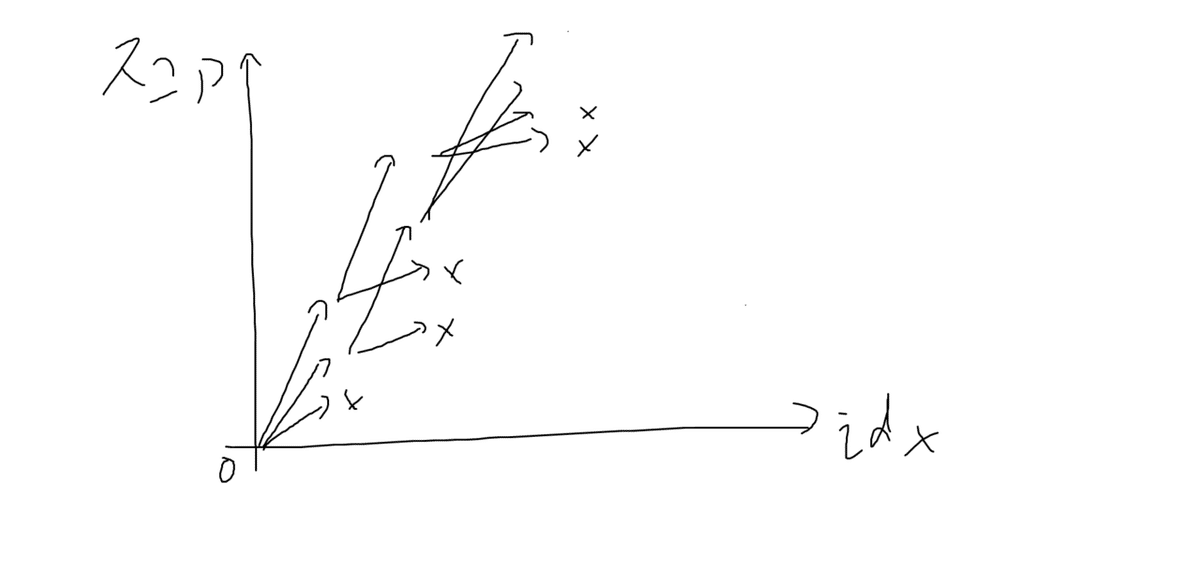
解配列のidx番目の値を埋めるとき、とりあえず全てのパターン(場合によっては乱択も可)を試します。その中で上位M個(この定数Mをビーム幅と言います)選んで、選んだM個それぞれの状態について、idx+1番目を埋めます。その後、またスコア上位M個選び、同じことを繰り返します。擬似コードにすると以下になります。わかりやすさ重視のため、少し効率が悪い疑似コードです。
def scoring(state):
return stateのスコア
states = [[初期スコア, 初期状態]] # 基本的には初期状態は空の配列になると思います
for idx in range(解の長さ):
next_states = []
for _, state in states:
for num in 考えうる手:
next_state = copy(state)
next_state.append(num)
# next_statesにスコアと次の状態を入れておく
next_states.append([scoring(next_state), next_state])
next_states.sort() # スコアが良い順にソートする
states = [] # statesを初期化
for next_state_idx in range(min(ビーム幅, len(next_states)):
score, next_state = next_states[next_state_idx]
states.append([score, next_state])ビームサーチでは貪欲法以上に良い解が得られます。貪欲法では、例えば「解配列の要素idx番目までではあまりスコアが良くないが、そのあと挽回して最後にはとてもスコアの良い解になる」といった場合には対応できません。ビームサーチでは上の「あまりスコアが良くない」と書いた部分が、その時点での他の解とあわせて上位M個に入っていればその後も探索を続けられます。
当然ですが、ビームサーチではビーム幅が大きければ大きいほど良いスコアの解が出力されます。実際には実行制限時間やメモリ制限との兼ね合いがあるのでビーム幅は無難な値を設定することになります。
ビーム幅の弱点は色々ありますが、その中の一部を改善したものにchokudaiサーチというものがあります。アルゴリズムとしてはビームサーチとは別物ですが、ビームサーチと似た場面で使えます。この記事では触れませんが、chokudaiさんの書いたわかりやすい記事があるので貼っておきます。
ビームサーチのポイントは以下です。
初期にビーム幅未満しか状態がないなら無駄にビーム幅まで状態を増やさない
上の擬似コードで、min(ビーム幅, len(next_states))と書いた部分があります。ここについての話です。例えば一つの状態から考えうる次の状態が10個あり、ビーム幅が1000の場合、最初の3要素を埋めるまでは、考えうる全ての状態数がビーム幅より少ないです。ここで無理にstates配列にビーム幅ぶんの要素を持つようにしようとしてstates配列に同じ状態を複数入れてはいけません。そうするとせっかく大きなビーム幅を持っていても中身を見ると同じ状態が大量に存在することになってしまいます。
状態をいちいち保持しない
前述と似た話ですが、上の疑似コードでnext_statesは必ずしも完璧な状態配列を含む必要はありません。例えば、元となる状態のインデックスと、次の手として選んだ値であるnumを保持するだけでも良いです。
statesの更新のときに少し処理が面倒になりますが、この方が圧倒的に高速に、そしてメモリも少なくなります。ビームサーチは時間とメモリの両方がネックとなるアルゴリズムだと思います。なるべく両方の面で軽くしましょう。
最後にビームサーチが活躍した問題と私の提出です。
この問題で私は記事執筆時点の全提出で10位の点数を保持しています。
遺伝的アルゴリズム
私自身実際のコンテストの問題で使ったことはないのですが、場合によっては使えるかもしれないので書いておきます。
これまで紹介してきたアルゴリズムが一つのとても良い解を作るアルゴリズムなのに対し、遺伝的アルゴリズムはたくさんの解で構成された集団の底上げをするアルゴリズムです。
遺伝的アルゴリズムは、生物が交叉して子孫を作っていく仕組みに着想を得たアルゴリズムです。
遺伝的アルゴリズムではまずたくさんの解(ここでは個体と呼びます)を基本的にはランダムに作ります。そして2個体を選んで、「遺伝子を混ぜ」、子供を作ります。例えば解が配列で表されるなら、子供の配列の各要素は親1と親2のどちらかからとってきたものにします。そして子供を親にして、また同じように交叉させていきます。たまに突然変異として解配列の要素を一つランダムに変えたりします。
遺伝的アルゴリズムは多様性を武器にして解を洗練していくアルゴリズムです。
遺伝的アルゴリズムには様々な実装方法がありますので、それを踏まえたポイントをまず書いて、最後に擬似コードを載せます。
子供の作り方
親の出来が良ければたくさんの子供を作り、出来が悪ければ少ない子供を作る、という実装方法がありますが、これでは極端に集団の中でスコアの高い親の遺伝子が大量の子供に受け継がれ、遺伝的アルゴリズムの肝である多様性が失われることがあります。こうなると局所解にハマる危険性があるのです。私のおすすめは2つの親を選んだら子供を必ず2つ作ることです。
世代間での交叉もできるようにする
遺伝的アルゴリズムでは、世代を超えての交叉を許す場合と許さない場合があると思いますが、私は許した方が良いと思っています。一つの問題で試験的にしか遺伝的アルゴリズムを使ったことがありませんが、世代を超えての交叉を許したほうが点数が上がりました。また、世代を区切らないと時間管理が楽になることが多いと思います。
親を必ずしも子供で置き換えなくても良い
最初の説明ではわかりやすく、子供を必ず受け入れて親に昇格させるような書き方をしましたが、必ずしもそうする必要はありません。ここまでに解説したポイント2つを実装すると、親2つから、子供と親をあわせて4個体が生成されます。この4個体のうちからスコアの良い2個体を選んで、元の親と同じ場所に格納すると良いと思います。
遺伝的アルゴリズムは局所探索が苦手
遺伝的アルゴリズムは多様性でスコアを上げるアルゴリズムです。よって、「良い感じではあるが解空間の近くにもっと良い解がある」といったことが頻繁におきます。それを回避する私がやっている方法は、子供を作ったときに子供に軽い焼きなまし法を行うことです(実際には親にも子供よりさらに軽い焼きなまし法をかけたりもします)。こうすることで、世代を重ねるごとに焼きなまし法の試行回数が増えていき、自然と局所探索もされた解ができあがります。
最初の親はランダムに作ったほうが良い
最初の親を作る場合、貪欲法を使いたくなる人もいると思います。ですが、遺伝的アルゴリズムは多様性が大事です。貪欲法を使うと往々にして解の多様性があまりなくなってしまいます。最初の親はランダムに作るのが良いと思います。
では私が使う実装方法を擬似コードで示します。
def anneal(state):
stateに対して焼きなまし法を行う
parents = [ランダムにN個分解を作る]
while 経過時間 < 制限時間:
parent1_idx = ランダムに選んだ親1のparents配列内のインデックス
parent1 = parents[parent1_idx]
parent2_idx = ランダムに選んだ親2のparents配列内のインデックス
parent2 = parents[parent2_idx]
child1 = 親1と親2の子供
child2 = 親1と親2の子供
anneal(child1) # 子供1に軽い焼きなまし
anneal(child2) # 子供1に軽い焼きなまし
parents[parent1_idx] = 親2つと子2つの中で1番目にスコアが良いもの
parents[parent2_idx] = 親2つと子2つの中で2番目にスコアが良いもの
経過時間を更新する
この実装を見た上でさらにポイントですが、遺伝的アルゴリズムも高速化が命です。山登り法と焼きなまし法で書いたのと同じポイントを意識すると良いと思います。
遺伝的アルゴリズム+他のアルゴリズム
くどいようですが、遺伝的アルゴリズム単体はたくさんの解で構成された集団の底上げをするアルゴリズムです。
この特徴のために遺伝的アルゴリズム単体でヒューリスティック問題に対して有効な場合はあまりないと思います。しかし、この特徴をうまく使い、他のアルゴリズムと組み合わせるととても良い解が得られることがあります。
例として、解のスコアは正負どちらにもなり、0に近いほど良いという問題を考えましょう。また、解配列を半分で切り、小解配列2つに分けたとしても解配列として機能し、分けたそれぞれでスコアが計算でき、さらに、解配列全体のスコアは小解配列のスコアの和であるとします。
2つの小解配列についてそれぞれ遺伝的アルゴリズムを施して、「それなりに良いスコアを持つ小解配列」がたくさん得られたとしましょう。便宜上2つに分けた小解配列のi番目をそれぞれAiとBiとします。
小解配列の集合Aと、別の小解配列の集合Bのそれぞれi番目、j番目の小解配列AiとBjを取ってくるとします。例えばAiは-10点というスコアを持っていて、Bjは+11点というスコアを持っているとします。問題設定により、解全体のスコアは小解配列AiとBjのスコアの和です。足してみると、AiとBjをくっつけた解のスコアは-10+11=1点です。スコアは0に近いほど良いので、このスコアはかなり良いです(AiやBjのスコアよりも0に近づきました)。
このように、解配列を複数個に切って、それぞれ遺伝的アルゴリズムでたくさんそれなりに良い解を作ると、小解配列の選び方によってはスコアがうまく相殺して、最終的なスコアがとても良くなる場合があります。
このように、遺伝的アルゴリズムは単体ではあまりヒューリスティックコンテストには使えないかもしれませんが、問題との相性や工夫次第では大きな力を発揮することもあると思います。まあそんな問題に出くわしたことは今のところないのですが…
ゲームAIコンテスト編
ここから先はゲームAIコンテストについてです。
全体像
ゲームAIコンテストの多くはいかに多く探索を進めるかで勝敗が決まります。
ゲームの多くは自分がこう行動して、相手がこう行動して…という連続で進んでいきます。これをいかに先読みするかでそのゲームAIの強さがかなり決まります。
また、ゲームはその状態(盤面など)の評価が難しいからこそゲームなのですから、いかにその状態を評価するかでも強さが決まります。しかし、評価関数を作る体系的な手法はないので、この記事では探索アルゴリズムについて解説します。
探索アルゴリズムについて、各アルゴリズムの関係性を図にして紹介します。

大きく分けてminimax法から派生したアルゴリズムとモンテカルロ木探索があります。しかし、私は記事執筆時点でモンテカルロ木探索に詳しくないので(詳しくないから派生アルゴリズムがあるのかも知らないのですが)この記事ではminimax法系のアルゴリズムについて書きます。
それではここから探索アルゴリズムについて詳しく見ていきましょう。
minimax法
あなたがゲーム(2人でやることを想定します)をプレイするとして、何を考えながらやるでしょうか。基本的には、「自分がこういう手を打ったら相手はこう打ってきて、そうしたらこう打とう…」みたいに考えると思います。
これをもう少し具体的に考えましょう。
自分はもちろん自分が考える自分にとって最善の手を打ちます。相手はどう打ってくるでしょうか。相手は相手にとっての最善手=自分(私)にとって一番不利な手を選んで打つのではないでしょうか。そして、どの手が良くてどの手が悪いかは自分で決めるしかないので、結局、ゲームは以下の繰り返しになります。
先手: 先手にとって一番有利な手=後手にとって一番不利な手を選ぶ
後手: 先手にとって一番不利な手=後手にとって一番有利な手を選ぶ
これ以外の場合は必ずこの場合よりも有利になるため、考えなくても良いです。
実際にゲーム木(ゲームが進むにつれて出てくる盤面をノードにした木)を描いて考えてみましょう。
前提として、minimax法ではゲーム木の葉(深さNまで先読みするなら、深さNのノード(=盤面))でしか評価値を計算しません。私がminimax法を理解する上で引っかかったところなので明示的に書いておきます。
ではゲーム木を描いてみましょう。

ゲーム木はこのような見た目をしています。現在の盤面からどんどんと手を進めていって、末端(事前に決めた深さN)のノードで評価値を、別途評価関数を自分で用意して計算します。
この図の例では3手先まで読むことにしていて、一番下のノードで評価値を数字で表しています。評価関数の作り方に決まりはありませんが、基本的には0なら互角、負なら自分が不利、正なら自分が有利となるようにします。
また、ここも躓きポイントなのですが、minimax法での評価値は必ずAI視点で作ります。コードを書いているとだんだん「これはAI視点なのか相手視点なのか、どっちで評価すれば良いんだ…」となってしまうので最初に書いておきます。
さて、末端ノードで評価値を得たら、次はこの評価値をどんどん深さの浅い(図だと上方向の)ノードに反映していきます。この反映のしかたにminimax法の真髄があります。
前述の通り、
先手: 先手にとって一番有利な手=後手にとって一番不利な手を選ぶ
後手: 先手にとって一番不利な手=後手にとって一番有利な手を選ぶ
という流れでゲームは進んでいきます。これを「AI」と「相手」という言葉で書き換えましょう。
AI: AIにとって一番有利な手を選ぶ
相手: AIにとって一番不利な手を選ぶ
これを先ほどのゲーム木に適用してみましょう。

末端ノードはたくさんありますが、その1つ上のノードであるD、E、Fで採用する評価値はそれぞれ1つずつです。例としてノードDで採用する評価値を考えてみましょう。DからG、DからHは共にAIが操作する番です。よって、GとHで評価値が高い方(AIに有利な方)の評価値を選びます。よって、ノードGの評価値である5をノードDに適用します。同じようにしてノードEにはIの評価値10を、FにはKの-2を適用します。
これでノードD、E、Fに適用する評価値が得られました。次はBとCの評価値を考えましょう。

ノードB、Cから伸びる辺は相手が操作する番です。よって、AIにとって一番不利な手による評価値を採用します。ノードBについて考えれば、Bから伸びるノードDとEのうち、評価値の低い方を採用します。よってBで採用する評価値はノードDの5となります。同様にしてノードCで採用する評価値は-2です。
さて、これで次にどの手を選べば良さそうなのかが明らかになりました。BとCで評価値が高い方に向かって手を打てば良いです。つまり、ノードBに向かって手を打ちます。
ここまで具体例を使ってminimax法を紹介しましたが、これをコードに落としてみましょう。擬似コードです。
class board:
def expand():
return そのnodeから到達できる全てのノードの集合
def next_player():
return 次のプレイヤー
def evaluate(node):
return nodeのAIプレイヤーにとっての評価値
def minimax(node, depth, player):
if depth == 0:
return evaluate(node)
next_player = node.next_player()
if player == ai: # aiの番: 評価値が一番大きい手を選ぶ
val = -inf # とても小さい値で初期化
for next_node in node.expand():
val = max(val, minimax(next_node, depth - 1, next_player))
else: # 相手の番: 評価値が一番小さい手を選ぶ
val = inf # とても大きい値で初期化
for next_node in node.expand():
val = min(val, minimax(next_node, depth - 1, next_player))
return valnegamax法
negamax法はminimax法の実装が違うだけのバージョンです。上の擬似コードを見るとわかると思うのですが、if文でvalのmaxとminを変えています。これをなくすのがnegamax法です。
negamax法では、評価値の正負を逆にすればAIにとっての評価値だったものが相手にとっての評価値に早変わりするという性質を使います。
擬似コードを見るのが早いと思うので早速見てみましょう。
class board:
def expand():
return そのnodeから到達できる全てのノードの集合
def next_player():
return 次のプレイヤー
def player():
return 手番を持つプレイヤー
def evaluate(node):
return nodeのnode.player()にとっての評価値
def negamax(node, depth):
if depth == 0:
return evaluate(node)
val = -inf # とても小さい値で初期化
for next_node in node.expand():
val = max(val, -negamax(next_node, depth - 1)) # negamax関数にマイナスがついている
return valポイントは2つあります。
evaluate関数でminimax法ではAIにとっての評価値を返していたものが、negamax法ではそのノードで手番を持つプレイヤーにとっての評価値を返します。
また、negamax関数内でnegamax関数を再帰呼び出しする際にマイナスがついています。これを先ほどゲーム木と同じ図にして考えてみましょう。

これが評価値が求まった状態です。末端ノードで手番を持つのは相手なので、minimax法で使った評価値にマイナスがついています。
この評価値にマイナスをつけたものの中で一番値が大きいものをノードD、E、Fに適用します。言葉にするとなんだか複雑ですのでコードを参考にしてください。適用するとこうなります。

そしてまたこれらの評価値にマイナスをつけたもののうちの最大値をノードBとCに適用しましょう。

ノードBとCの評価値にマイナスをつけたときの最大値(つまり最小値)を持つノードが一番良さそうな手の先にあるノードです。minimax法と同じ結果になりましたね。
追記したい内容
私の力が途中で尽きたことにより、とりあえずalpha-beta法、nega-alpha法、MTD-f法、nega-scout法はまた今度追記することにします。
また、私があまり理解していないという理由でモンテカルロ木探索を書けませんでしたので、いつか追記したいです。
他にも「これ書いてくれ!」とか「ここ間違ってる!」とかありましたらコメントやらTwitterのDMやらメンションやら飛ばしてください。
今文字数を確認したら17000字超えていました。長いですね…次のアップデートでは2万字を突破しそうな勢いです。
