
NIRSの信号処理について考えてみる〜⑦GLMによる波形の近似〜
NIRSについての記事は今回がラストかなー。
これに関しては小野先生のテキスト[1]に倣ってやっているからコードは記載しないということで。
これまでとの違い
⑥までの記事では,得られた波形に対してノイズを除去したり関心のある周波数帯域の信号を抽出したりという,観測された波形そのものにアプローチしていた。
一方で,今回の方法は得られた波形に対して直接何かをするのではなく,モデル関数を定義して,実際の波形に対するモデル関数の当てはまりを見るというもの。
つまりあれだよ。回帰分析だよ。
HRFによるモデル化
ここで大変というか考えないといけないのは,モデル関数がどのようなものになるのかということ。
もちろん単純な線形モデルになるわけではなく,例えばブロックデザインだとRestとTaskの繰り返しを考えて,Taskのタイミングで波形の山ができて,Restでは波が落ち着くというような周期関数に近い形になる。
さらに,血流変動データの場合は単純な正弦波の形にはならず,血流動態反応関数(HRF: Hemodynamic Response Function)という,あるタイミングで瞬間的に脳活動が生じた際の血流信号の時間変化を模したものが考えられている。
NIRSデータに対しては,このHRF(とブロックデザインのモデル)を使ってモデル化する。
実際にやってみる
ここでは,Rest (20 sec) → Task (20 sec)を9回繰り返すブロックデザインを想定してやってみる。HRFとブロックデザインのモデル波形はこんな感じになる(図1)。なお,ブロックデザインの縦軸は本来は0か1かでしかないことには注意(単にこの図の作り方がよろしくない)。

次に,実際のNIRSデータに対する脳活動のモデル関数を作るために上の2つを畳み込む。そうするとこんな感じの波形になる(図2)。

これでモデル関数の完成…と思いきや,実際のNIRSデータにはベースラインが全体的に正もしくは負の値にずれたり,時間が経つにつれて上昇したり(これがドリフト)するものもある。
これも考慮する必要があるので,脳活動のモデル関数のほかに,ベースラインシフトのモデル関数とベースラインドリフトのモデル関数も作成する。これらは例えばこんな感じ(図3)。
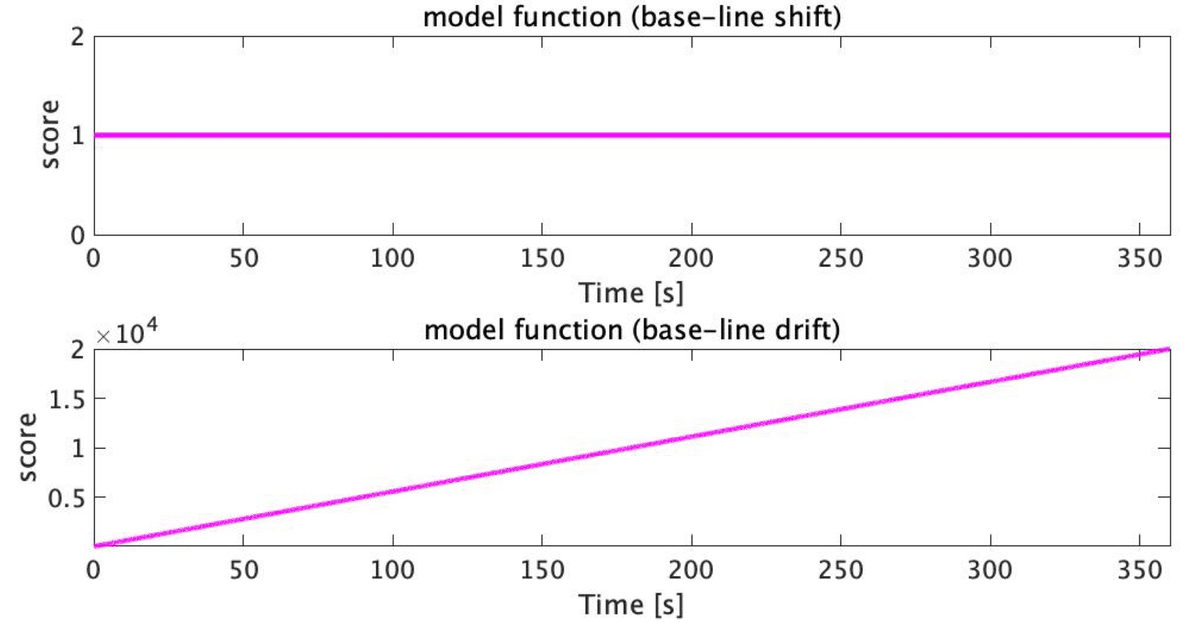
それで,ここまでの3つを使って実際のNIRSデータを説明してみようということになる。具体的には図4の通り(この記事で言いたいことはここだけ)。

回帰分析がわかればこれも特に問題なく理解できるかなと。
これを条件別にとか群別にとかやって,注目したい要因の効果を調べるという流れになるのかな。
実際のNIRSの信号に対して周波数云々を調べたりフィルタリングしたりという作業をしないというのは簡単かもしれないけど,次のような点には注意が必要かな。
モデル関数による近似の結果であるため,実際の脳活動の結果とは異なる可能性がある。
(上に関連して)実際の波形は得られない(rawデータは別として)。
例えば複数の条件がランダムな順序で設定されている場合は,各データの条件に応じてモデル関数を作成する必要がある。
刺激や計測領域などによってはHRFのパラメータを調整する必要がある。
個人的には,⑥までのように実際の信号から目的の波形を得るという方法を使う方が好きかなー。
最後に,HRFについてだけど,これはSPMが必要になる。これはwebで検索すれば色々なバージョンのものが公開されているので,自分の実行環境に応じて導入してほしい。HRFのパラメータについては図5の通り(これ僕もわからない部分が多いから,詳しい方がいたら教えてほしい)(これ図というより表かな?)。

NIRSデータの処理についてはこんな感じ。長々とお疲れさまでしたー。
参考文献
[1] 小野弓絵 (2018) MATLABで学ぶ生体信号処理,コロナ社,pp117-122
