見出し画像

NIRSの信号処理について考えてみる〜④フーリエ変換からウェーブレット変換へ〜

N.

さあ今回も「ざっくりと」やっていきましょー。


フーリエ変換の限界と短時間フーリエ変換

前回の記事でフーリエ変換にも限界があるよーという話をしたけど，これはフーリエ変換をすると時間情報が失われてしまうというもの。

具体的には，振幅の情報と時間の情報があったものを振幅の情報と周波数の情報に変換するから，「どの周波数の波がいつ発生したのか」がわからなくなってしまう（図1）。

図1　フーリエ変換の限界

これを改善したものが「短時間フーリエ変換」。

どういうものかというと，「いつ」の情報もほしいなら「変換する範囲を区切ってしまえばよくない？」というもの。具体的には図2のような感じ。こうすればどのタイミングでどの波が発生しているのかがわかる。

図2　短時間フーリエ変換のイメージ

これで万事解決だね…と思いきやそうでもない。

例えば，波の変化をもっと細かく見たいからといって変換の時間幅を狭めると，周波数の検出性能が低下（周波数分解能が低下）してしまう。

これは「不確定性関係（不確定性原理）」と呼ばれ，具体的には「時間分解能と周波数分解能はトレードオフの関係にある」というものだが（図3），数学的に内在する問題であるために解決する方法はないとのこと。

図3　フーリエ変換における不確定性関係のイメージ

Q. 「トレードオフ」ってなんぞや？
A. 一得一失。時間を細かく調べようとすれば周波数情報が大雑把になるし，周波数を細かく調べようとすれば時間情報が大雑把になる。


時間も周波数も知りたい欲張りな方のために

実際に周波数解析をしてみると，時間情報と周波数情報って常に同じくらい重要というわけではないことが多くて，高周波帯域では時間情報を細かく見たいし，低周波帯域では周波数情報を細かく見たくなる。それぞれの特徴を考えてみれば「そうだよねー」ってなると思う（図4）。

図4　時間を優先するか周波数を優先するか

図4のように，周波数に応じて分解能を変化させるという都合のいいことが「ウェーブレット変換」だとできる。

ウェーブレット変換について，数学的な話や厳密なことは僕も理解し切れていない難しいのでいつものように要点だけざっくりと説明する。

何をするかというと，基底関数（ベースとするもの）としてマザーウェーブレットという波のかけらを決めて（←これは色々とあってそれぞれに特徴はあるものの，明確な選択基準があるわけではないとのこと），これを解析したい波に対して「シフト（平行移動）」と「スケーリング（拡大縮小）」を繰り返して解析対象との相関をとっていく（図5）。

図5　ウェーブレット変換をものすごく簡単にまとめるとこんな感じ

もっと簡単に言えば，高周波→低周波という流れで調べる時だと，

  • マザーウェーブレットを決めます。

  • マザーウェーブレットをぎゅっと縮めます。

  • 縮めたマザーウェーブレットを解析対象の波の始まりから終わりに向かって平行移動させながら，マザーウェーブレットと解析対象の波との各部分での類似性を見ます（図6）。

  • 最後まで行ったら縮めたマザーウェーブレットを少し伸ばしてまた同じことをします。

  • これを繰り返します。

図6　マザーウェーブレットのシフトのイメージ

図6は動画の方がわかりやすいかなと思うので，以下の動画（10:45–11:16の部分）を紹介します（この部分について，左側だけじゃなくて右側も何気に重要）。

「YouTube 【Andrew Nicoll】The Wavelet Transform for Beginners」


さらに細かく言えば，マザーウェーブレットのシフトとスケーリングを連続的に行う「連続ウェーブレット変換（CWT: Continuous Wavelet Transform）」と，これを離散的に行う「離散ウェーブレット変換（DWT: Discrete Wavelet Transform）」に分けられるんだけど，この辺は簡単に説明できるほど理解し切れていないので「ざっくりと」の範囲を超えてくるから特徴だけまとめておく（図7）。

図7　CWTとDWTの特徴の比較


実際にやってみよう

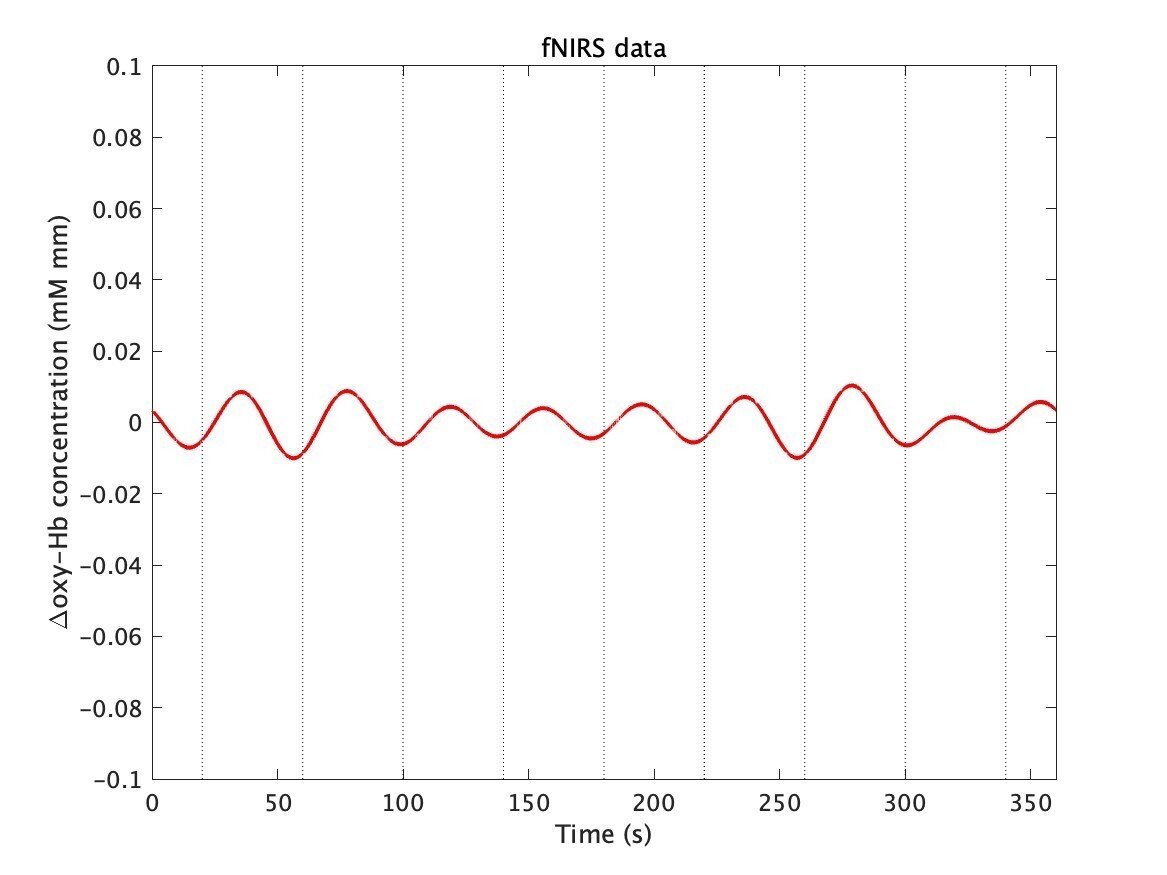
じゃあ実際にNIRSデータを用いてどんな周波数の波がいつ発生したかをMATLABで調べてみようというで，わかりやすくするために実際のNIRSデータを綺麗にしたものをサンプルとして使ってみる。これは前回までと同様に応答成分が約0.025 Hzのデータで，さらにこの付近の成分を含むように元のデータ（諸々の処理前のデータ）から特定の帯域の成分を抽出したもの（図8）。

図8　サンプルデータ

MATLABのヘルプセンターを参考に，スカログラム（時間–周波数解析の結果の図の一種）を出力する。はいどーん（図9）。

図9　サンプルデータ（図8）のスカログラム

（ちなみに短時間フーリエ変換でも同じような図を作ることができるんだけど，短時間フーリエの場合は「スペクトログラム」で，ウェーブレットの場合は「スカログラム」なんだとか）

図9を見てみると，0–360秒にかけて一貫して約0.025 Hzの成分が含まれていることがわかる。さらに振幅との関係に注目すると，図8で振幅が大きめのところでは図9でも振幅が大きいものとして表示されている。あと図8で微妙に変な波になっている部分では図9でもかなり低い周波数成分が含まれているとされている。

いやー，これは便利だね。何がいつ発生したかが一目で分かる。

ちなみに，図9の白い線は「円錐状影響圏（cone of influence）」の境界線で，ここよりも外側の部分は結果が歪んでいる可能性があるから注意してねということを示している。

なんで結果が歪むかは図6を見てみると気付くかなと。マザーウェーブレットが一部しか表示されてないでしょ？だからマザーウェーブレットとの相関が綺麗に取れない。あと低周波帯域だとマザーウェーブレットは横長になっているから，データの両端だと表示されない部分が大きくなる。だから低周波帯域の円錐状影響圏は高周波帯域よりも大きくなる…と僕は解釈している。

さてさて，今回は図9のようなスカログラムを出力するコードを載せて終わろうかな。次回は多重解像度解析について書く予定。

x＝data;

num = 1:length(x);
sig = x(num, 1);
fb = cwtfilterbank('SignalLength', length(x), 'SamplingFrequency', Fs);
[cfs, frq, coi] = wt(fb, sig);
t = (0:length(x)-1)/Fs;
pcolor(t, frq, abs(cfs));
shading interp;
hold on
plot(t, coi, 'w-', 'LineWidth', 2)
hold off
xlabel('Time (s)')
ylabel('Frequency (Hz)')
c = colorbar;
c.Label.String = 'Magnitude';
ylim([0.01 0.1])
title('Scalogram')

このコードだと，マザーウェーブレットは"Morse"を使うみたい。
あとFsは前回までと同じくサンプリング周波数ね。


まとめ

厳密には色々と足りない・間違っているかもしれないけど，簡単にまとめると以下の通りかな。

  • フーリエ変換：どんな波が含まれているかがわかります。

  • 短時間フーリエ変換：どんな波がどこに含まれているかがある程度わかります。

  • ウェーブレット変換：どんな波がどこに含まれているかが結構いい感じにわかります。

…ね？ざっくりしているでしょ？


参考文献



いいなと思ったら応援しよう！