超難問を解く(その1)
問題
川合秀実さんの数独研究のページで最も難しいと紹介されている問題を解いてみます(SE11.7)。
⇒ 川合秀実の数独研究に関するドキュメント #01
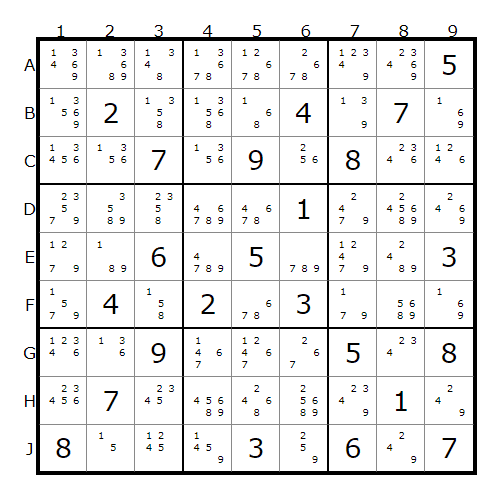
解き方(概要)
解き方の概要は次の通りです。記号の意味はあとで説明します。
-68DF5 → 47DF5 89E46 → 矛盾
∴[68]DF5
-47DF5 → 68DF5 [24]H5
2H5 → 矛盾
4H5 → 矛盾 (+-1C9 → 1A3)利用
∴[47]DF5
[47][68]DF5
-47E46 → 89E46 [24]E8
2E8 → 矛盾
4E8 → 矛盾
∴[47]E46
-89E46 → 47E46 -47DF5 矛盾(既出)
∴[89]E46
[47][89]E46
-39GJ8 → 24GJ8
→ 矛盾 (+-1C4 → 1J3)(+-2D9 → 2H3)利用
∴[39]GJ8
-24GJ8 → 24H79
→ 矛盾 (+-1C1 → 6F9)(+-4C8 → 4J3)利用
∴[24]GJ8
[24][39]GJ8
[24][39]H79
2E8 → 矛盾 (+-2A5 → 4G1)利用
4E8 → 解ける (+-2J3 → 2C9)利用
8E8 → 矛盾 (+-8D2 → 58H46)利用
9E8 → 矛盾
説明
では 順に説明します。
-68DF5 → 47DF5 89E46 → 矛盾
∴[68]DF5
DF5に 68がどちらも入らない とすると 矛盾が起きます。
この場合 47DF5 89E46 で
このあと 基本手筋で解いていくと 矛盾が起きることがわかります。
それで DF5のどちらかに 68どちらか が入る とわかります。
記号の意味
DF5: セルD5 と セルF5 を結合した領域
47DF5: DF5に47が入る
-68DF5: DF5に68が入らない
[68]DF5: 6または8が DF5に入る
-47DF5 → 68DF5 [24]H5
2H5 → 矛盾
4H5 → 矛盾 (+-1C9 → 1A3)利用
∴[47]DF5
DF5に 47がどちらも入らない とすると 矛盾が起きます。
この場合 68DF5 [24]H5 となりますが、
2H5のときは 基本手筋だけで 矛盾が起きることがわかります。
4H5のときは DFCで 1A3 がわかります(詳細は後述します)。
あとは 基本手筋で 矛盾が起きることがわかります。
それで DF5どちらかに 47のどちらか が入る とわかります。
DFC:
あるセルに ある数字が 入るか入らないか の2択で推論します。
DFCは Digit Forcing Chains の略です。
今の場合は 68DF5 なので 1B5 になり
4H5 から 4GJ8 14A7.C9 2AC8 2H79
24G1.J3 1GJ3 14C19
また [89]E2 [89]E8 89E28 7E6
[12]E1 124CEG1 -14A1 -14A2 14A37
すると
1C9なら 1A3、-1C9でも 1F9 1A3 で
必ず 1A3 とわかります。
このように
1C9 と -1C9 から 1A3 を確定する ような推論を
DFC と呼びます。
記号の意味
A7.C9: セルA7 と セルC9 を結合した領域
+-1C9: 1がC9に入るか入らないか の2択
+-1C9 → 1A3:
1C9 または -1C9 どちらの場合も 1A3 になる
[47][68]DF5
DF5には 47のどちらか と 68のどちらか が入る とわかります。
-47E46 → 89E46 [24]E8
2E8 → 矛盾
4E8 → 矛盾
∴[47]E46
E46に 47がどちらも入らない とすると 矛盾が起きます。
この場合 89E46 [24]E8 となりますが、
2E8のときも 4E8のときも、
基本手筋で 矛盾が起きることが わかります。
それで E46どちらかに 47のどちらか が入る とわかります。
-89E46 → 47E46 -47DF5 矛盾(既出)
∴[89]E46
E46に 89がどちらも入らない とすると 矛盾が起きます。
この場合 47E46 -47DF5 となりますが、
これは矛盾が起きます(説明は前述しています)。
それで E46どちらかに 89のどちらか が入る とわかります。
[47][89]E46
E46には 47のどちらか と 89のどちらか が入る とわかります。
-39GJ8 → 24GJ8
→ 矛盾 (+-1C4 → 1J3)(+-2D9 → 2H3)利用
∴[39]GJ8
GJ8に 39がどちらも入らないとすると 矛盾が起きます。
この場合 24GJ8 となりますが、
[89]E8 で [89]E46 なので 1E2 5J2
24A7.C9 1B79 で [68]B5
[68]DF5 なので [24]H5 58H46
6H1 167G456
+-1C4 から 1J3
(1C4なら 1G5 1J3,
-1C4 なら 1C1 1J3)
+-2D9 から 2H3
(2D9なら 2H3,
-2D9なら 2C9 4D9 4H5 4G1 2H3)
あとは 基本手筋で 矛盾が起きることがわかります。
それで GJ8どちらかに 39のどちらか が入る とわかります。
-24GJ8 → 24H79
→ 矛盾 (+-1C1 → 6F9)(+-4C8 → 4J3)利用
∴[24]GJ8
GJ8に 24がどちらも入らない とすると 矛盾が起きます。
この場合 24H79 24G1.J3 1GJ2 [89]E2
となりますが、
[89]E46 なので [24]E8
[68]H5 [68]DF5 1B5
[24]E8 なので 1[24]A7.C9 39B78 58DF8
+-1C1 から 6F9
(1C1なら 1F3 6F9,
-1C1なら 1C9 6F9)
+-4C8 から 4J3
(4C8なら 4E4 4J3,
-4C8なら 4C1 4J3)
あとは 基本手筋で 矛盾が起きることがわかります。
それで GJ8どちらかに 24のどちらか が入る とわかります。
[24][39]GJ8
[24][39]H79
GJ8には 24のどちらか と 39のどちらか が入る とわかります。
H79には 24のどちらか と 39のどちらか が入る とわかります。
2E8 → 矛盾 (+-2A5 → 4G1)利用
2E8のとき 矛盾が起きます。
4GJ8 で 24A7.C9 1B79 [68]B5
[68]DF5 2H79 で 4H5 24G1.J3
+-2A5 から 4G1
(2A5なら 2C9 9H9 4J8 4G1,
-2A5なら 2G5 4G1)
あとは 基本手筋で 矛盾が起きることがわかります。
4E8 → 解ける (+-2J3 → 2C9)利用
4E8のとき 矛盾なく 最後まで解けます。
2GJ8 で 24A7.C9 1B79 [68]B5
[68]DF5 4H79 で 2H5 24G1.J3
+-2J3 から 2C9
(2J3なら 9J8 4H9 2C9,
-2J3なら 2D3 2C9)
あとは 基本手筋で 最後まで解けます。
8E8 → 矛盾 (+-8D2 → 58H46)利用
8E8のとき 矛盾が起きます。
[89]E46 で 1E2 5J2
+-8D2 から 58H46
(8D2なら 8F5 58H46,
-8D2なら 8A2 8H6 5H4)
9J46 [24]J8 3J8
あとは 基本手筋で 矛盾が起きることがわかります。
9E8 → 矛盾
9E8のとき 矛盾が起きます。
[89]E46 で 1E2 5J2
[24]J8 で 3J8
あとは 基本手筋で 矛盾が起きることがわかります。
まとめ
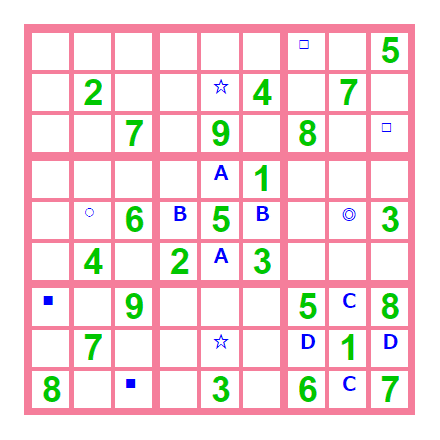
この問題は、
AA BB CC DD を中心に ☆☆○◎□□■■に特徴的な構造があり、
◎の候補を調べ ると 解くことができます。
