
ケーキを横に切る理系少年たち
こんにちは、hachchchです。
今回はケーキを横に切って三等分する方法を考えたのでそれを説明する試みです。
「ケーキを三等分する問題」の話を知っている方は本題から読むことをおすすめします。
ケーキの切れない非行少年たち
突然ですが、
「ケーキの切れない非行少年たち」という話をご存知ですか?
これは児童精神科医の宮口幸治氏が勤務経験を下に著した書籍で、非行少年たちはケーキを等分に切ることができなかったという話が有名です。
僕が中学生のとき、ケーキを三等分に切らせる問題がある種のIQテストとして流行っていました。
ケーキを三等分する
一般に、ケーキを三等分に切る切り方はこういう切り方になります。

こんな感じに切り目をY字のようにするのが正しい切り方です。
これで三等分できていることを簡単に説明します。
上の図は切り目が全て中心を通っていて、別の切り目に対する角度は120°になっています。
円の角度は360°なのでケーキを120°の3つに切り分けている上の図はケーキを三等分に切れていることがわかりますね。
それに対して非行少年たちの切り方は多くの場合中心を通らず横に切ったりしています。

(切り目の線がちょっと歪んでるのは気にしないで)
切り目の間隔は均等ですが、真ん中の部分の面積は明らかに大きいです。
横に等しい間隔でケーキを切った場合、真ん中の部分の面積は他の部分の面積の約2.3倍になってしまい、3等分にはなりません。
本題
ここまではケーキの切れない非行少年の話で、ここからが本題、数学の時間になります。
先ほど、ケーキを三等分する方法はY字の形に切り分けると言いましたが、面積が三等分になればいいので本当は横に切って三等分する方法があるのではないでしょうか。
実際、積分を用いることで半円の面積を計算することが可能なので、
積分区間を3つに分けてどこからどこまで切れば三等分になるのかを計算できそうです。
円の方程式から計算する
円を描く関数は$${x^2+y^2=r^2}$$(rは半径)と習ったはずです。
そしてこれをyについて解くと、$${y=\pm\sqrt{r^2-x^2}}$$となります。これは半円を描く関数で、正のときyの値が円の中心以上における半円を描きます。

横に切る場合、切り目は左右対称になるので正負どちらかの面積を三等分に切れればいいでしょう。
半円の積分
ここからは半円を積分していきます。
半円の方程式をf(x)とおいて、$${2\int_{-r}^{r}{f(x)dx}}$$を計算することで円の面積になるでしょう。
今回はケーキを3つに切り分けるわけですから積分区間をa,b,rとおいて計算をしたいです。
まず、$${\int_a^b{\sqrt{r^2-x^2}dx}}$$を計算する必要があります。
根号を含む積分は置換積分を用いてうまいこと根号を外すのがセオリーです。
そこで、$${x=rsinθ}$$と置きましょう。
すると$${\sqrt{r^2-x^2}}$$は$${\sqrt{r^2-r^2sin^2θ}}$$になり、これは$${rcosθ}$$に変形します。
また$${dx=rcosdθ}$$、積分区間a,bは$${arcsin(\frac{a}{r}),arcsin(\frac{b}{r})}$$になり、
積分は$${\frac{r^2}{2}\int_{arcsin(\frac{a}{r})}^{arcsin(\frac{b}{r})}{(1-cos2θ)}dθ}$$になります。
これを計算すると$${\frac{r^2}{2}[θ+\frac{sin2θ}{2}]_{arcsin(\frac{a}{r})}^{arcsin(\frac{b}{r})}}$$です。
なんだか$${arcsin(\frac{a}{r})}$$がごちゃごちゃするので丸ごとA,Bと置きましょう。
ちなみに$${rsinA,rsinB}$$でa,bを求めることができます。
最終的に$${\frac{r^2}{2}(B+\frac{sin2B}{2}-A-\frac{sin2A}{2})}$$となります。
これで、積分区間A,B($${-\frac{π}{2}≦A,B≦\frac{π}{2}}$$)における半円の面積を求める関数を作ることができました。
3等分できる間隔を求めよう
さっきの関数を用いてa,bからb,rまでの面積が同じことを表す方程式を立てましょう。
そして、その方程式は
$${4B+2sin2B-2A-sin2A=π}$$
です。
後はA,Bを求めればいいだけです。
灯台下暗し
しかし、ここで筆者は苦戦します。
問題はこの方程式はA,B2つの変数が残ったままです。
いろいろな方法を用いてA,Bについて解こうとしましたが行き詰まってしまいました…
しばらくここで諦めかけていたところ、半円はy軸に左右対称であるということをなんとか思い出し、A=-Bとおけることを考えつきました。
考えてみれば簡単なことですが無駄に時間をかけてしまいました。
結果
さあAを-Bに置き換えようということで、
この方程式は$${6B+3sin2B=π}$$になります。
ここまで計算できれば後はコンピューターに任せるだけ。
一応マクローリン展開して3次方程式の解の公式を使えば手計算で近い値を出せそうですが日が暮れてしまいます。
Bは約0.268になりました。
ラジアンである0.268を$${b=rsinB}$$に代入し長さのbに変換するとだいたい$${0.265r}$$です。
つまり中心から縦に半径×0.265[m]の位置に横向き切れ目を入れ、
中心から縦に-半径×0.265[m]の位置にもう一つ横向き切れ目を入れてできる3つの面積が同じ、すなわち$${y=0.265r,-0.265r}$$がケーキを三等分する切れ目の線というわけです。
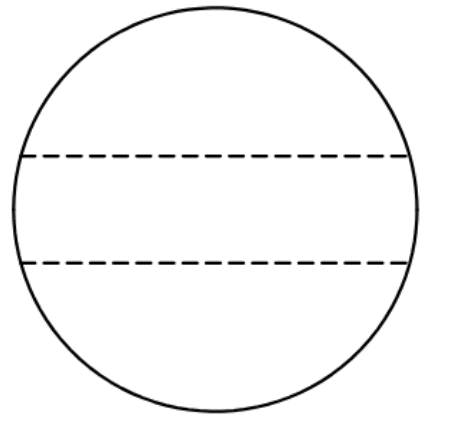
やったぜ
実際に面積は三等分になっているのか?
しかし喜ぶのはまだ早いです。
実際に面積を求めてみなければ三等分になっているかは分かりません。
では、先程の半円の方程式を積分して面積が3等分になっているか確かめてみましょう。
$${\int_{-0.265r}^{0.265r}\sqrt{r^2-x^2}dx=2\int_{0}^{0.265r}\sqrt{r^2-x^2}dx}$$
$${=2\int_{0}^{0.268}r^2cos^2θdθ}$$
$${=r^2[θ+\frac{sin2θ}{2}]^{0.268}}$$
$${=0.523r^2}$$
$${=\frac{π}{6}r^2}$$
となりました。
ここで$${πr^2}$$は円の面積の公式ですね。
それを2で割ると半円の面積、そして更に3で割る(円の面積公式を6で割る)と半円の面積の3分の1です。
しっかり面積を3等分できています!
横に切って三等分は不公平?
これで、横に切ってケーキを三等分する方法がわかりましたが、
実際に試さないほうがいいと思います。
なぜなら、ケーキは放射状にいちごやクリームが配置されていることが多く、3次元的に考えると体積が異なる場合が多いです。
ということで実用的には放射状にも対称なY字に切った方が争いが少なくなるというのが結論です。
