
量子力学を概観する(6)「光と量子論」
量子力学は古典力学と並ぶ物理学の2本柱の一つです。
これらはミクロ/マクロの物理学として区別され,量子力学はミクロ=原子などの微粒子の運動を表すことができます。
本連載では,数式の導入などは行わず,量子力学とは何かを概観していきます。
学問の勉強というよりは手軽に読んでいただけるような読み物を目指していきます。
今回のテーマは「光と量子論」です。
光のエネルギー
波としての光
光のエネルギーは非常にシンプルな数式で示すことができます。
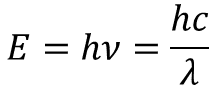
ここでhはプランク定数,cは光速なので定数です。
つまり,光のエネルギーは振動数や波長の逆数に比例します。
特に重要となるのは波長との関係です。
粒子としての光
さて,以前の記事で粒子と波は異なる性質を示すものの同一であるということをお話ししました。
先ほどの光のエネルギーは振動数や波長の逆数に比例するとお話ししました。
これらのパラメータは連続な値をとります。
光を波と考える(=古典力学で考える)と当然の結果です。
しかし,粒子のエネルギーは連続な値をとらず,離散的な値しかとらないことになっています。
まず,光は光子という粒子で考えることにします。
量子力学ではこの粒子1つ1つに着目してエネルギーや波動関数を考えています。
光子1つの運動エネルギーを計算すると次のようになります。

ここでmcは光子の重さです。
では光子の重さはどれくらいでしょうか?
正解は「光子に重さは存在しない」,つまり0となっています。
まぁ,実際は限りなく0に近いだけでわずかに重さはあるはずです。
ですが,限りなく0に近いというのがポイントで,光子1つのエネルギーは限りなく0に近いと言えます。
これは波としての光のエネルギーと矛盾していますよね?
ここにはいろいろな解釈があると思いますが,のうむなりの解釈をさせていただきます。
まず,先ほど計算した運動エネルギーは光子1つのエネルギーです。
一方の波としての光のエネルギーの式は,光子1つの話ではありません。
つまり,個々にエネルギーを持つ光子の集団が波としての光と解釈すれば,光子のエネルギーの総和をとり,マクロに見ると連続的になるということです。
光のメカニズムの前に
ヤブロンスキー・ダイアグラムは光のメカニズムを説明するのに最も有用な方法です。
その前にスピン多重度の概念を知る必要があります。
電子と軌道
スピン多重度の前に軌道と電子の話をします。
以前に波動関数の話をした際に,s軌道やp軌道といった話をしました。
電子の入る軌道は複数種類あり,それは異なるエネルギーを持つことになります。
今はややこしいので,原子にできる軌道(原子軌道)のみを考えます。
(分子軌道は分子軌道理論やボルンオッペンハイマー近似などで考える必要があり,話が膨大になるため割愛)
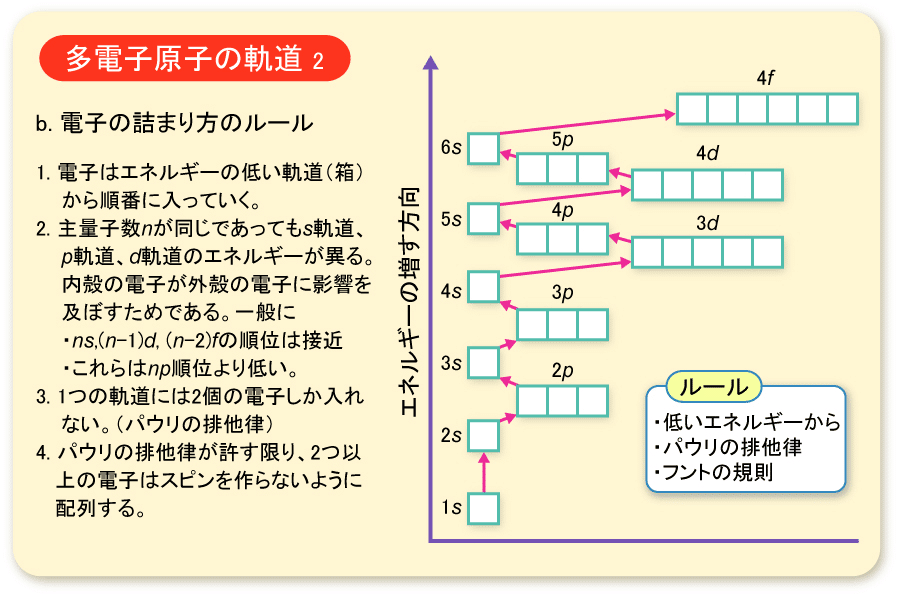
まあ,d軌道は5つ全て等価ではなく,原子や電子状態で大きく変化するんですが・・・(このあたりは以前の記事をご参考に)。
電子はエネルギーの低い軌道に入っていきますが,2つのルールに基づいて軌道が決められます。
・Pauliの排他原理
・フント則
Pauliの排他原理
パウリの排他原理(パウリのはいたげんり、英: Pauli exclusion principle)とは、2つ以上のフェルミ粒子は、同一の量子状態を占めることはできない、という原理である[1]。
Wikipediaにも書かれている通り,各軌道に入ることのできる電子の数は2つまでです。
2つ入る場合も,電子スピン(upとdownの2種類がある。磁石のS極とN極,電荷のプラスとマイナスのような関係。)は必ず逆向きになります。
電荷で例えると,プラス同士の電荷が狭い場所に2つ入るのは静電反発(斥力)で不安定だが,プラスとマイナス同士であれば引力なので安定というイメージです。
フント則
軌道には2つまで電子が入れると話しましたが,同じエネルギーの軌道が複数ある場合(p軌道やd軌道など),電子はなるべく別の軌道に入るようになります。
例えば,2人までは入れる部屋が3つ,3人いる場合,3人はバラバラの部屋に入るほうが広く使うことができますよね?
イメージとしてはそのような感じです。
スピン多重度
次にスピン多重度の話をしましょう。
まず,電子の数が偶数の場合,原子軌道に電子を占有していくと次のようになります。
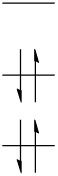
この状態をS0と呼びます。
ここから1電子が1つ上のエネルギー準位に移ったとしましょう。
すると軌道図は以下のようになります。
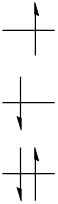
この状態をS1と呼びます。
高いエネルギーの電子のスピンが反転することもあります。
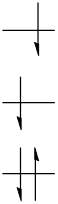
この状態をT1と呼びます。
これらS0,S1,T1のことをスピン多重度と言います。
それぞれ同じ電子数ですが,状態ごとのエネルギーは異なり,S0<T1<S1となっています。
一般にS0は最も安定な電子状態であることから基底状態,S1やT1はエネルギーが高くなった状態であることから励起状態と呼びます。
光を量子論で考える場合,この基底状態と励起状態が重要になってきます。
ヤブロンスキー・ダイアグラムと行きたいところだけど・・・
ここらの基礎があれば,ようやく光のメカニズムやヤブロンスキー・ダイアグラムについて説明できます。
が,ここまででかなりのボリュームになってしまったので次回に回します。
(前後編の予定はなかったけど)
少し複雑なところはかなり簡略的に解説してきましたが,ここらは光化学の基礎として重要な部分です。
光化学の成書などで詳しく書かれているので,興味のある方はそちらをご覧ください。
(もちろん,コメントで質問も歓迎します)
それでは,また。
