
量子力学を概観する(3)「シュレディンガー方程式」
量子力学は古典力学と並ぶ物理学の2本柱の一つです。
これらはミクロ/マクロの物理学として区別され,量子力学はミクロ=原子などの微粒子の運動を表すことができます。
本連載では,数式の導入などは行わず,量子力学とは何かを概観していきます。
学問の勉強というよりは手軽に読んでいただけるような読み物を目指していきます。
今回のテーマは「シュレディンガー方程式と波動関数」です。
シュレディンガー方程式とは?
シュレディンガーの猫
今回のテーマである「シュレディンガー方程式」の前に,以前の記事の紹介をさせていただきます(笑)。
「シュレディンガー方程式」って何なのさ?
では本題に移ります。
大学で物理や化学を専攻してきた人はご存じと思いますが。
そもそも「シュレディンガー方程式」って何なのさ?
と言う人も多いと思うます。
シュレディンガー方程式は条件(難しく言うと,次元数,時間依存かどうか,運動の種類など)により細かくは変化していきますが,大きくまとめると全て以下の式で表現できます。
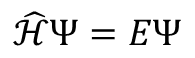
この式におけるEはエネルギー,ハミルトニアン(Hみたいなやつ)は演算子と言います。
演算子とは簡単に言うと計算の指示みたいなもので,微積分の記号(d^2/dx^2など)です。
「微積分なんてわかんねーよ」と言う人に説明するなら,足し算や引き算の記号(所謂「+たす」や「−ひく」)と同じと考えてもらって大丈夫です。
シュレディンガー方程式に戻ります。
残りの記号ψは「波動関数」です。
波動関数とは,電子や原子がどのような空間に存在するかを示す関数で,化学の場合は電子の位置=分子軌道を考えます。
つまり,シュレディンガー方程式は波動関数=電子の位置=分子軌道を求めるために使う方程式です。
波動関数(分子軌道)を求める目的は?
ではなぜ波動関数(分子軌道)を求める必要があるのでしょうか?
その例をいくつか紹介していきます。
その1:分子の反応点がわかる
分子軌道は1つではなく,ことねるエネルギー準位でいくつか描けます。
エネルギー準位ん低い順に電子が入っていくので,電子の入る最も高いエネルギー準位の軌道(HOMO:High Occupied Molecular Orbital)と電子の入らない最もエネルギーの低いエネルギー準位の軌道(LUMO:Low Unoccupied Molecular Orbital)が存在します。
Dield-Alder反応をはじめとしたフロンティア軌道理論に基づく反応では,HOMOやLUMOが重要になり,分子中の反応点が決まります。
また,芳香族化合物の場合,置換基効果によりベンゼン環上のどの炭素上にHOMO/LUMOが分布するかが変化します。
一般に求電子反応は電子豊富な場所で進行しますが,これは最もエネルギーの高い電子が存在する位置であるHOMOのある位置で反応が進行します。
その2:分子の分極もわかる
さきほどのHOMO/LUMOの話は,分極の説明もできます。
わかりやすい例がカルボニル基です。
カルボニル基は炭素がδ+,酸素がδ-の分極を形成しています。
実際のカルボニル基はHOMOが酸素上,LUMOが炭素上に多く分布しています。
波動関数と確率密度
既にお話しした通り,波動関数は電子の分布を表す関数です。
しかし,その関数(分子軌道)の中で存在しやすい場所=確率密度が存在します。
この確率密度は波動関数を2乗することで求められます。
これをグラフ化するとわかりやすいです。
まず,1s,2s,2p軌道の波動関数を考えてみましょう。

波動関数のグラフ
波動関数をグラフ化したものが以下になります。
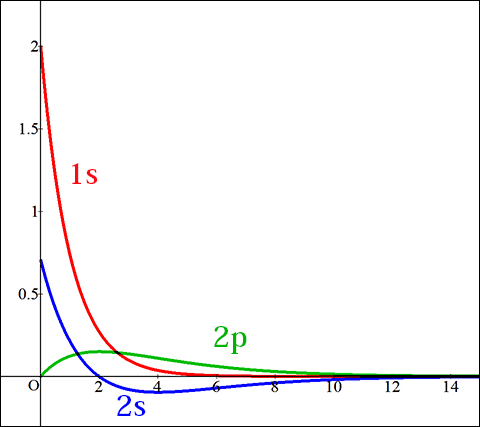
このグラフは横軸が座標(分子軌道の中心からの距離),縦軸が関数の強度(≒分布している割合)です。
なお,縦軸が負になっているものがありますが,これは位相が異なることを示しており,電子が存在しないというわけではありません。
確率密度のグラフ
確率密度は名の通り「確率」なので,正の値しかとりません。
そのため,2乗することで縦軸が正の値しかとらなくなります。
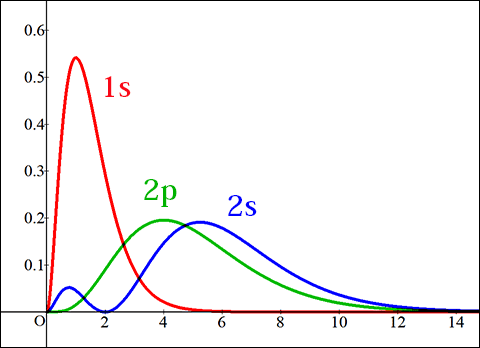
このように,軌道によってどの位置に電子が存在しやすいかが全く異なってきます。
1s軌道は中心に近い位置に存在しやすく,同じ形状の2s軌道は1s軌道より外側の方が存在しやすくなります。
まとめ
今回は「シュレディンガー方程式と波動関数」についてお話してきました。
講義などではシュレディンガー方程式の数式の導入や1次元ポテンシャツなど様々な計算?のようなことをしますが,個人的にはなぜシュレディンガー方程式が重要かを講義でも話したらいいのになと思っております。
そのため今回は,シュレディンガー方程式が波動関数を求めるということ,その波動関数が何に重要なのかをお話してきました。
ざっくりとシュレディンガー方程式が何かを知るきっかけになれば幸いです。
それでは,また。
