
量子力学を概観する(5)「量子ドット」
量子力学は古典力学と並ぶ物理学の2本柱の一つです。
これらはミクロ/マクロの物理学として区別され,量子力学はミクロ=原子などの微粒子の運動を表すことができます。
本連載では,数式の導入などは行わず,量子力学とは何かを概観していきます。
学問の勉強というよりは手軽に読んでいただけるような読み物を目指していきます。
今回のテーマは「量子ドット」です。
イントロダクション
「量子ドット」を取り上げたわけ
今回は少し趣向を変えて量子力学のアプリケーションを取り上げます。
アプリケーションといえば量子コンピュータが有名ですが、のうむ自身あまり詳しく無いのと、他に詳しい解説している所も多い(と思う)ので、量子ドットをテーマにしました。
井戸型ポテンシャルの解説
量子ドットについて紹介する前に井戸型ポテンシャルについて簡単に解説します。
数式を解いたりはせず、初見の方が大雑把にどのようなものかを知ってもらうため、少しのうむなりの解釈も加えています。
井戸型ポテンシャルは時間に依存しない1次元のシュレディンガー方程式に関するモデルです。
シュレディンガー方程式については過去記事をご覧ください。
井戸型ポテンシャルではまず1次元の軸(つまりはx軸)を考えます。
この軸上の0からLまでの範囲に電子が存在すると仮定します。
電子が存在できない範囲は電子が入れない高エネルギーな空間(V=∞)と考えます。
一方、0からLの範囲では自由に電子が存在し得るので周りにエネルギーがほとんどないとします(V=0)。

さて、仮定で述べたように、電子は0からLの範囲に存在します。
この範囲内における確立密度の合計(積分)は1になります(確立密度については以前解説したので割愛します)。
電子はこの空間を動き回りますが、0やLの近くでは高エネルギーの空間に近いため、電子は反発して存在しにくくなります。
つまり0やLに近づくにつれ、確立密度は0に近づきます(ただし、0にはならない!)。
つまり波動関数を書くと次のようになります。
(nの値は主量子数ですが、粒子のエネルギーのようなものです。)
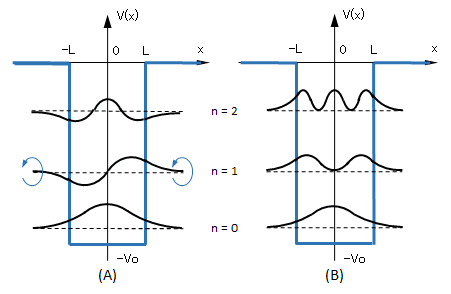
と簡単にはこのようになります。
細かく解説すると量子ドットの話ができなくなるのでここまで。
量子ドットについて
そもそも量子ドットとは?
話を量子ドットに戻しましょう。
量子ドットについて、Wikipediaには次のように書かれています。
量子ドット(りょうしドット、英: Quantum dot (QD)、古くは量子箱)とは、3次元全ての方向から移動方向が制限された電子の状態のことである。
と少し難しい表現だと思います。
先ほど解説した「井戸型ポテンシャル」を3次元に拡張したものが量子ドットです。
言葉では分かりにくいと思いますので写真で見てみましょう。

https://www.sigmaaldrich.com/JP/ja/products/materials-science/energy-materials/quantum-dots
どうですか?
綺麗ですよね。
量子ドットはどのように使われるのか?
では量子ドットは何に使われるのでしょうか?
まず、このように綺麗な単色光を出せることからレーザーへの応用が挙げられます。

また、綺麗な発光を生かし、LEDにかわる新たなディスプレイ材料としても期待されています。
発光色をそのまま生かせるので、有機ELと同じような色の鮮やかさやエネルギー効率、薄型化など特徴です。
どうやらQLEDと呼ばれているみたいです(のうむも最近まで知りませんでした)。

量子力学の観点から見た量子ドット
量子ドットは3次元にした井戸型ポテンシャルと紹介しましたが、もう少し深く見て見ましょう。
量子ドットは半導体の一種と考えることができます。
そのため、エネルギーや発光特性については、半導体と同じバンド理論で説明できます。
(バンド理論は固体物理学や無機化学の分野なので、本連載では解説を省略します。)
量子ドットが半導体と異なる点は、大きさです。
量子ドット1つの大きさは、ド・ブロイ波長と同程度の数nmほどでとても小さいです。
その大きさの違いにより、発光色が変化します。

https://www.nanosysinc.com/quantum-dot-basics/
量子ドットの構造
少し量子力学から離れた観点ですが、量子ドットの構造についてみていきましょう。
量子ドットは所謂コア–シェル構造を持ちます。
つまり、CdSeなどのコアに有機分子などからなるシェル構造の2つからなります。
先ほど量子ドットの大きさで発光色が変わると言いましたが、厳密にはコアの大きさと言えます。

まとめ
今回は量子力学のアプリケーションとして「量子ドット」について紹介してきました。
量子力学が実生活でどのように役立つのか、現代科学としてどのような研究が行われているのかについて知っていただけたかと思います。
本連載「量子力学を概観する」では、このようなトピックについても取り上げていこうと思っております。
それでは、また。
