ノーマルタイプのパチスロの連チャンとハマリのゲーム数を定義する
機種ごと設定ごとに、連チャンやハマリのゲーム数を明確に定義します。
はじめに
この記事では、ノーマルタイプのパチスロの「連チャン」と「ハマリ」についての、私なりの定義をご紹介したいと思います。
ホールのデータ表示機には100ゲーム以下の当たりが連チャンとして表示されます。しかし、”機種や設定にかかわらず一律でよいのか？” という疑問を私は抱きます。
一方、ハマリの表示はありません。何となく、”300ゲームを超えたらハマリで、600ゲームを超えたら大ハマリかな～？”と私は感じます。
そこで、この記事では「連チャン」や「ハマリ」を私なりに明確に定義しようと思います。具体的には、当選確率を基にしてゲーム数を定義します。
最終的には、機種ごと設定ごとに、連チャンやハマリのゲーム数が明確に定義されます。
成果として、設定推測や波読みに役立てたり、連チャンやハマリの発生の仕組みを理解できるようになります、
また、連チャンやハマリの議論は前提が曖昧なために噛み合いにくいという印象を受けます。その打開策になればとも思います。
最後までお付き合い頂ければ幸いです。
連チャンとハマリの定義（大枠の定義）
※ あとで細分化した定義をしますので、今は大枠です。
早速ですが、私は連チャンとハマリを以下のように定義したいと思います。
２回に１回の頻度(=50%)で発生する早い当たりを、連チャンと定義する
10回に1回の頻度(=10%)で発生する遅い当たりを、ハマリと定義する
100回に1回の頻度(=1%)で発生する遅い当たりを、大ハマリと定義する
ゲーム数ではなく確率で定義するわけです。
この定義に従えば、ボーナス確率によって、すなわち、機種や設定によって、連チャンやハマリのゲーム数は変わります。
台の設定が分からないから意味がないと思われますか？そんなことはありません。
たとえば、設定6のハマリの定義を台の履歴に当てはめてみます。台のハマリの頻度が10%より明らかに多ければ、設定は6より低いだろうと推測できます。（あくまで活用方法の一例です）
※ 当たりはBIGとREGの両方とし、ボーナス確率はBIGとREGの合成確率（合算確率とも言います）とします。
※ ゲーム数の起点（0ゲーム目）はボーナス終了直後、もしくは朝一とします。
具体例
では、連チャンは何ゲームまでで、ハマリは何ゲームから、になるのでしょうか？
ボーナス確率が分かっていれば、計算で求めることができます。（計算方法は後で説明します。）
例として、キングハナハナ30の設定5で計算してみましょう。ボーナス確率は1/145です。
計算結果は、
100ゲーム以下での当選は連チャン
334ゲーム以上での当選はハマリ
666ゲーム以上での当選は大ハマリ
となります。
次に、マイジャグラーVの設定6で計算してみましょう。ボーナス確率は1/114.6です。
計算結果は、
79ゲーム以下での当選は連チャン
264ゲーム以上での当選はハマリ
526ゲーム以上での当選は大ハマリ
となります。
いかがでしょうか？ 実戦での感覚にまあまあ合致しているのではないでしょうか。
計算の仕方
※ 数式が嫌いな人は、次の大見出しまで読み飛ばしてかまいません。
連チャンやハマリのゲーム数の計算方法を説明します。長くなりますので、前半と後半の２段階に分けて説明します。
計算方法（前半）
ボーナス確率が1/145のケースを例にします。この場合、当たらない確率は 144/145 です。
100ゲームの間に一度も当たらない確率は、
となります。
「一度も当たらない」の否定は、「少なくとも一度は当たる」です。
否定ですから、全体の確率（=1）から上記の確率を引きましょう。
これは、100ゲームまでに少なくとも一度は当たる確率です。
このように、「～ゲームまでに少なくとも一度は当たる確率」を求めたい場合は、「～ゲームまで当たらない確率」を計算して、１から引けばよいのです。
上の式をExcelで計算すると、答は0.499になります。
つまり、当選確率が1/145の場合に100ゲームまでに当たる確率（※1）は約50%、になります。
※１の補足
”100ゲームまでに少なくとも一度は当たる確率” は、”100ゲームまでに当たる確率”、と言い換えてよいのです。なぜなら、実戦では、ボーナス終了時点でゲーム数を0にリセットし、そこから新たにゲーム数のカウントを始めるからです。
計算方法（後半）
上で示したのは、あるゲーム数までに当たる確率を求める式でした。
実際に欲しいのは、これとは逆に、確率を与えてゲーム数を求める式です。
まず、ゲーム数をNとして、これまでと同じ式を書いてみましょう。
確率をPと書きます。
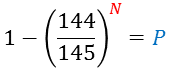
より一般化するために、当選確率を 1/q と書きましょう。当選確率が1/145ならq=145です。当たらない確率 は 1-1/q と書けます。
この式の意味は、
”当選確率が1/qの場合にNゲームまでに当たる確率はPである ”
ということです。
この式をいじくると、次の式を導くことができます。
欲しかった式はこれです。
※導出は巻末の参考記事1をご参照ください
式(1)を使えば、確率Pを与えてゲーム数Ｎを求めることができます。
※ ExcelのLOG関数を使えば楽に計算できます。
連チャンの最大ゲーム数を計算したい場合は、式(1)のPに0.5(=50%)を代入してゲーム数Nを求めます。50%の確率（2回に1回の頻度）でそのゲーム数までに当たる、ということになります。
ハマリの最小ゲーム数を計算したい場合は、Pに0.9(=90%)を代入してNを求め、そのNに1を足します。
Nゲームまでに当たる確率は90%ですから、N+1ゲーム以上で当たる確率は10%（10回に１回の頻度）になるというわけです。
連チャンとハマリの定義（細分化した定義）
連チャンとハマリを、もう少し細分化して定義し直します。
連チャンは、連チャン1と連チャン2のふたつに分割します。
ハマリは、その深さによって複数に分類します。
まずは、具体例を見ていただきましょう。
グラフに「超劇ハマリ」は表示していません
小ハマリ、ハマリ、大ハマリの右端は無限です
表の赤字部分は説明に使います。
グラフに「超劇ハマリ」は表示していません。
小ハマリ、ハマリ、大ハマリの右端は無限です
※ グラフでは「連チャン1」「連チャン2」を「連1」「連2」と略しています。これ以降も、しばしば略して書きます。
表の見方を説明します。
キングハナハナ30の設定5を例にします。図1bで赤字にしている行です。
連チャン1： 1～42 ゲーム
連チャン2： 43～100 ゲーム
中間： 101～200 ゲーム
小ハマリ： 201 ゲーム以上（無限まで）
ハマリ： 334 ゲーム以上（無限まで）
大ハマリ： 666 ゲーム以上（無限まで）
超劇ハマリ： 999 ゲーム以上（無限まで）
という意味になります。
「連チャン2」と「中間」の最初のゲーム数は、前の区間の次のゲームであることにご注意ください。
※キングハナハナ30の設定5を例に選んだのは、上のように分かりやすい数字が多く出てくるからです（それだけの理由です）。
（もしかしたらメーカーは意図して1/145という確率にしたのかもしれませんね。）
「区間」で当たる確率
細分化した定義の大きな特徴は、連チャンなどを区間で定義していることです。
そしてまた、連１～小ハマリの４つの区間での当選確率が、すべて等しく25%（＝1/4）になるように定義していることです。
※ したがって連１～小ハマリは、おおむね均等にランダムに発生すると期待されます。（もちろん、必ずそうなるとは限りません）
図にすると次のようになります。
大ハマリと超劇ハマリは省略した
図2の赤い数字は、その区間で当選する確率です。
（注記）正確に言うと、その区間の前までは当選せず、その区間で初めて当選する確率です。
区間で当選する確率の算出方法を説明します。
0ゲーム目を起点として各区間の境界のゲーム数までに当選する確率が下図の青い数字になるように、式(1)を使って各区間のゲーム数を決めます。
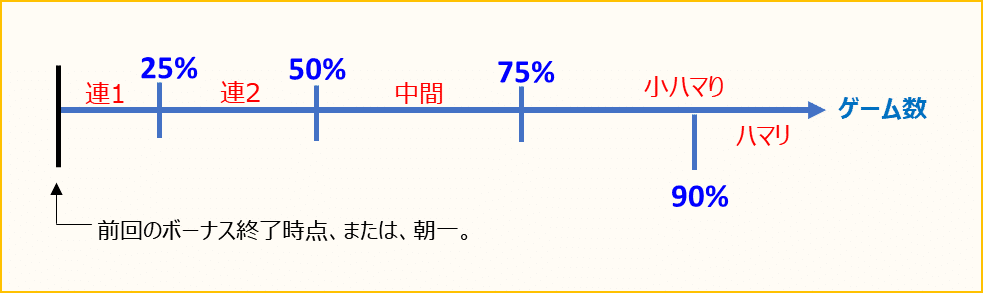
連チャンは連と略した。大ハマリと超劇ハマリは省略した。
各区間で当選する確率は、図3から以下のように算出できます（※2）。
「連2」の区間は、50%-25% = 25%
「中間」の区間は、75%-50% = 25%
「小ハマリ」の区間は、 100%-75% = 25%
「ハマリ」の区間は、 100%-90% = 10%
※２の補足 ： 引き算でよい理由
興味ある方だけ読んで頂ければ結構です。
外れる確率をaとします。例えば、当たる確率が1/145であれば、外れる確率aは144/145です。
下式の左辺は、200ゲームまでに当たる確率から100ゲームまでに当たる確率を引いたものです。
左辺は右辺に書き換えることができます。
右辺は、最初の100ゲームは当たらずに、次の100ゲームまでに当たる確率を意味しています。つまり、101ゲーム～200ゲームの区間で当たる確率というわけです。
区間の境界のゲーム数の算出
各区間の境界のゲーム数は、式(1)に下表のPを代入して計算します。「小ハマリ」より後は、求めたNに1を足すことに注意してください。
連チャンとハマリの定義（最終形）
さきほどの細分化した定義を、連チャンとハマリの定義の最終形とします。
この記事の冒頭に書いた大枠の定義との矛盾はありません。
整理して下に示します。
超超劇劇ハマリを追加した
図4のように定義することによって、機種ごとに設定ごとに連チャンやハマリのゲーム数が明確に決まります。前に示したマイジャグラーVとキングハナハナ30の定義表が具体例です。
実際の機種の連チャンやハマリのゲーム数（定義表）
別紙で実際の機種の定義表を公開しています。巻末の参考記事2をご参照ください。（無料or有料）
BIGのみ、REGのみ、の定義表も載せています。
式(1)を使えば誰でも計算できますが、手間賃と思って購入してもらえると嬉しいです。
キングハナハナ30とマイジャグラーVの定義表は無料ですので、ぜひご覧下さい。
Zone表：キングハナハナ30（無料）｜ワイボン ♡パチスロ (note.com)
Zone表：マイジャグラーV（無料）｜ワイボン ♡パチスロ (note.com)
注記： 参考記事2では定義表のことを「Zone表」と書いています。もともとは別の記事（参考記事３）のために作った資料で、その記事では「区間」のことを「Zone」と呼んだからです。Zoneは単に「区間」という意味で、当たりやすい区間という意味の「ゾーン」ではありません。
区間の当選確率が同じなのに、区間の長さが変わる理由
ここで、頭に刻み込んでおいてほしいことがあります。
「連1」、「連2」、「中間」、 「小ハマリ」のそれぞれの区間での当選確率はどれも25%です。しかし、区間の長さは等しくありません。
連1が最も短く、順に長くなっていきます。小ハマリに至っては長さは無限です。
以下に理由を説明します。
まず、～ゲームまでに当たる確率をグラフで見てみましょう。
ゲーム数が増加するにつれて、グラフの傾きは小さくなっていきます。
このため、区間の当選確率が同じ25%でも、区間の長さはだんだん長くなっていくわけです。
では、なぜグラフの傾きは小さくなっていくのでしょうか？
"～ゲームまでに当たる確率"は、"～ゲームまで当たらない確率"を１から引いて求めました。
よって、答は ”～ゲームまで当たらない確率” にあります。そのグラフは下のようになります。
このグラフの傾きは、なぜ小さくなっていくのでしょうか？
考えやすくするために、ボーナス確率を1/2としましょう。
当たらない確率は1/2ですから、Nゲームまで当たらない確率は、
と計算できます。
つまり、ゲーム数が１増えるごとに、そのゲームまで当たらない確率は、1つ前の確率の半分、半分、半分・・・となっていくのです。1/2が1/4に、1/4が1/8に、1/8が1/16に・・・となっていくわけです。
このため、グラフの傾きはだんだん小さくなっていくのです。
※ ボーナス確率が1/145の場合は、当たらない確率は144/145=0.993ですから、上の説明の「半分」を「0.993倍」に置き換えればいいです。
補足
実戦では、「ここまでハマったから、そろそろ当たるだろう」と思うことがあります。あるいは、逆に「ゲーム数が増えるほど当たりにくくなる」と感じることもあります。
一見、図5や図6が、その裏付けになっているように見えます。しかし、それは間違いです。
当選確率は常に一定です。（と私は前提しています）
どのゲーム数から始めても、０ゲームから始めることと同じで、始めたゲーム数から図5や図6のグラフが始まるのです。（ここは大事なポイントですので、この後で解説します）
確率の不思議ですよね・・。
どのゲーム数から始めても、０ゲームから始めることと同じということ
一言で言えば、「当選確率は常に一定」であることが、その理由になります。この説明で腑に落ちる人は、次の大見出しまで読み飛ばして頂いて構いません。
一方で、図5や図6のような特性を経験を通して実感していて、何となく納得できない人は（私はそうでした）、以下の説明をお読み下さい。
具体例として、500ゲームで捨てられている台を600ゲームまで打つ場合を考えてみましょう。
外れる確率をaとします。例えば、当たる確率が1/145であれば、外れる確率aは144/145です。
下式の左辺は、0ゲームから始めて600ゲームまで当たらない確率です。
左辺は右辺に書き換えることができます。
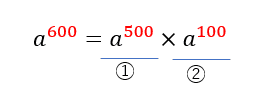
右辺の①は最初の500ゲーム当たらない確率で、②は次の100ゲーム当たらない確率です。
500ゲームから打ち始めた人は、②の部分だけを経験します。
②の部分は、0ゲームから始めて100ゲーム当たらない確率と同じです。
次に、0ゲームから始めて600ゲームまでに当たる確率を見てみましょう。下式の左辺がそれです。
左辺は右辺に書き換えることができます。（右辺を展開すれば左辺になることが分かります。）
右辺の③は、最初の500ゲームは当たらずに次の100ゲームで当たる確率です。そして、④は最初の500ゲームまでに当たる確率です。
これら２つの確率の和（式の右辺）が、0ゲームから始めて600ゲームまでに当たる確率（式の左辺）になるというわけです。（下図参照）
さて、500ゲームから打ち始めた人は、⑤の部分だけを経験します。
⑤の部分は、0ゲームから始めて100ゲームまでに当たる確率と同じです。
※ 自分自身が最初から打っている場合も、もちろん同じです。
以上のように、どのゲーム数から始めても、０ゲームから始めることと同じで、始めたゲーム数から図5や図6のグラフが始まると言えるのです。
補足
500ゲームから打ち始めた場合は、500ゲームまで当たらなかったことが確定していますので、①式の確率が1になっている、と考えてもいいです。(この説明の方が、数学的には正しいです。）
これに対して、0ゲームから打ち始めた場合は500ゲームまで当たらないことがまだ確定していませんので、500ゲームから始めた場合とは違う確率になるというわけです。
区間の確率を基に定義することのメリット
区間の確率を基に連チャンやハマリを定義することのメリットは何でしょうか？
第一に、設定推測に活用できるというメリットがあります。また、波読みにも活用できます。この記事では深掘りしませんので、興味のある方は巻末の参考記事3をご覧ください。
次に、機種や設定にかかわらない考察や議論ができる、というメリットがあります。
ボーナス確率の違いを各区間のゲーム数の違いに取り込んだあとは、「連チャン」や「ハマリ」という言葉だけで考察や議論ができるからです。
その結果、連チャンやハマリの発生の仕組みをシンプルに理解できるようになります。
連チャンやハマリの発生の仕組み
「連1」「連2」「中間」「小ハマリ」の各区間で当選する確率は、すべて等しく25%です。
従って、連チャンとハマリの発生の仕組みを、下図のような簡単なモデルで表すことができます。
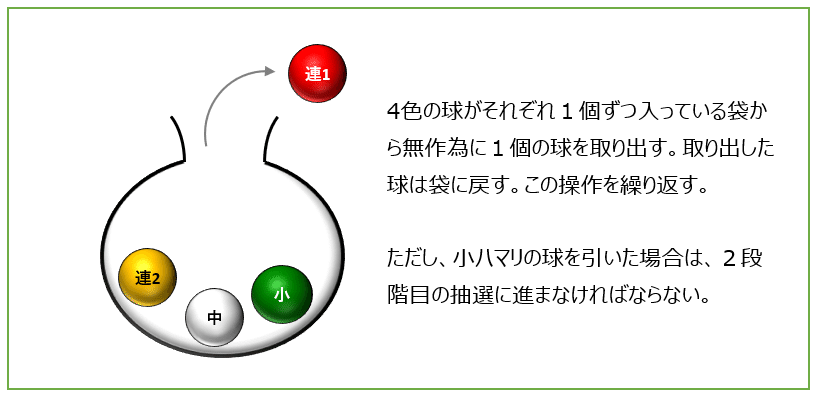
「中」は「中間」、「小」は「小ハマリ」
「小ハマリ」は、5回に2回の頻度で「ハマリ」に至ります。(10%/25%=2/5)よって、上の図のモデルで小ハマリの球（緑玉）を引いた場合は、下図に示す２段階目の抽選を受けなければなりません。
取り出した球の色の並びはランダムになります。例えば、下図のようになるかもしれません。
球のランダムな並びが、自然と、連チャンやハマリなどの「波」を生むわけです。
”連チャンやハマリの発生の仕組み”と大げさな言い方をしましたが、
連1、連2、中間、小ハマリがそれぞれ25%の確率でランダムに発生し、
ハマリが10%の確率でランダムに発生する
だけ、と考えればよいのです。
備考
以上は、あくまで一定の確率で抽選をしている（完全確率）という前提での私の見解です。
一方、意図的に連チャンやハマリが作られているという主張があります。私にはそれを検証する手段がありませんので、その主張が正しいとも間違っているとも言うことができません。
余談：実戦に役立つだろうこと
最後に、実戦に役立つだろうということをいくつか列挙したいと思います。
※ (2024/8/29）問題設定を間違えて説明していた箇所がありましたので削除しました。(2024/10/15) ハマリについての記述を追加しました。(2024/11/26） 連チャンが終わった後のハマリの確率ついての記述を追加しました。(2024/11/26）連チャン後のハマリとハマリ後の連チャンについての記述を修正しました。
連1と連2のどちらも連チャン。だから連チャンは連続しやすい。
ハマリは10%だから連続しにくい。（連続した場合は、低設定の定義を当てはめてみてください。実はハマリではないかもしれません。）
連チャンの次にハマリが来やすいわけでもなく、ハマリの次に連チャンが来やすいわけでもない。
※ ただし、連チャン（連1と連2）は50%で発生しますから、連1と連2の連続が終わった後にハマリが来る確率は10%の2倍の20%になります。「終わった」時点で、次に来るのは連チャン以外に確定しているからです。このために連チャンの後はハマリやすいと感じるのかもしれません。
ハマリは、ボーナス10回に1回の頻度で来る。いつも心構えをしておこう。
※ちなみに、ボーナスを10回、20回、30回、40回、50回と引くまで一度もハマらない確率は、35%、12%、4%、1.5%、0.5%となります。一度もハマらずに一日を終えることは至難の業です。
連1のゲーム数は、設定1から設定6までで大きく違わない。だから低設定でも早い連チャンが来る。（だから、だまされる・・。）
ハマリのゲーム数は設定差が大きい。低設定でもコインが増える場面があるが、ハマリで大きく減らされる。（これが低設定で負ける仕組み・・・。）
などなど・・
参考記事
参考記事1： Zoneの計算方法｜ワイボン ♡パチスロ (note.com)
参考記事2： Zone表一覧｜ワイボン ♡パチスロ (note.com)
参考記事3： パチスロの波を理論で読む: Zone Count（その１）｜ワイボン ♡パチスロ (note.com)
※ これらの参考記事では、区間のことをZone（ゾーン）と呼んでいます。
参考記事3から連チャンとハマリの定義だけを取り出して掘り下げたのがこの記事になります。この記事を一つの独立したものにしたかったので、Zoneという言葉は使わないようにしました。
まとめ
この記事では、連チャンとハマリについて、私が考える定義を紹介しました。ゲーム数ではなく確率を基に定義したものです。
最初に、大枠の定義を示しました。
次に、数学的な説明をしました。
次に、細分化した定義を示しました。当選確率に基づいてゲーム数を複数の区間に分割する定義です。これを最終形としました。再度、下に掲載します。
図4の定義に従えば、機種ごと設定ごとに連チャンやハマリのゲーム数が明確に決まります。
※ 実際の機種の定義表を参考記事2にて公開しています。ぜひご覧ください。
最後に、区間の確率を基に定義することのメリットを述べました。
そして、連チャンやハマリの発生の仕組みを、簡単なモデルを使って説明しました。
この記事が皆様のパチスロの理解や実戦のお役に立つことがあれば幸いです。
最後まで読んで頂き有り難うございました。
♡を押してもらえると素直に嬉しいです。