
新社会人のコスパのいい物件探し(物件価格予測)
のすけです。田舎から東京へ片道1時間半の通学がもうそろそろ終わる。最近は、卒論を書きながら統計や機械学習について自分でちょっと学んでいます。
就職先も決まり、来年からは東京の企業で社会人スタート。
そしてやっと一人暮らし。「電車からの解放」
大学時代はお金もなく、バイトは極力したくなかったので通学を頑張ってました。
そんなわけで
いい感じの物件でも探してみよ
と思い立ちまして、会社の近くの物件データを分析することに。
物件の条件
8万円以下(いろいろと事情がありまして・・・)
できるだけ会社の近くがいい
ということで
8万円以下かつ
江東区、大田区、品川区、港区、中央区、墨田区、江戸川区
にある物件データを集めてきました。
分析開始
ます、家賃と一番相関がありそうな専有面積をプロットしてみました。
部屋が広ければ、家賃も高いだろうということです。

もうちょっといい感じだと思ってた・・・
8万円以下という条件が最初からあったのでしょうがないですかね。。。
目的変数(家賃)の分布の確認


家賃の分布も上限までは若干、正規分布に従っていそうです。
予測モデル構築
今回は、回帰モデル構築をしたいと思います。
目的変数を'家賃'とし、
説明変数は,
"築年数", "階建", "階", "専有面積", "距離(最寄り駅からの距離)"
としています。
モデル構築の前に相関行列を見てみます。
回帰分析などの統計的モデリングにおいて多重共線性というものがあります。説明変数間の強い相関や線形従属が存在する場合に発生する問題です。具体的には、説明変数間の相関が高く、その結果としてモデルのパラメーター(係数)の推定が不安定になり、解釈が困難になることを指します。

・家賃と専有面積の相関係数が0.65とそこそこ高い正の相関がある
・家賃と専有面積の相関係数が0.55とそこそこ高い正の相関がある
・多重共線性は大丈夫そう
いよいよ回帰分析に入ります。上述した変数を用いてpythonモデルを構築しました。
model = sm.OLS(y_train,X_train) #OLS(ordinary least squares)最小二乗法
#計算結果をfitメソッドを使って変数resultsに代入
results = model.fit()
#分析結果を表示
results.summary()
OLS Regression Results
Dep. Variable: 家賃 R-squared (uncentered): 0.973
Model: OLS Adj. R-squared (uncentered): 0.971
Method: Least Squares F-statistic: 573.6
Date: Fri, 08 Dec 2023 Prob (F-statistic): 1.54e-60
Time: 09:50:53 Log-Likelihood: -132.05
No. Observations: 84 AIC: 274.1
Df Residuals: 79 BIC: 286.2
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
築年数 0.0224 0.020 1.111 0.270 -0.018 0.063
階建 0.0350 0.045 0.776 0.440 -0.055 0.125
階 0.0287 0.061 0.474 0.637 -0.092 0.149
専有面積 0.2714 0.021 13.102 0.000 0.230 0.313
距離 0.1016 0.047 2.146 0.035 0.007 0.196
Omnibus: 0.766 Durbin-Watson: 2.031
Prob(Omnibus): 0.682 Jarque-Bera (JB): 0.394
Skew: 0.149 Prob(JB): 0.821
Kurtosis: 3.153 Cond. No. 13.3
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.決定係数(Adjusted R-squared)は0.9以上で良さそうに見えますが、本当にこれでいいんですか?笑
外れ値をうまく弾かなかったことが原因なのでしょうか
とりあえず残差をプロットしてみます。

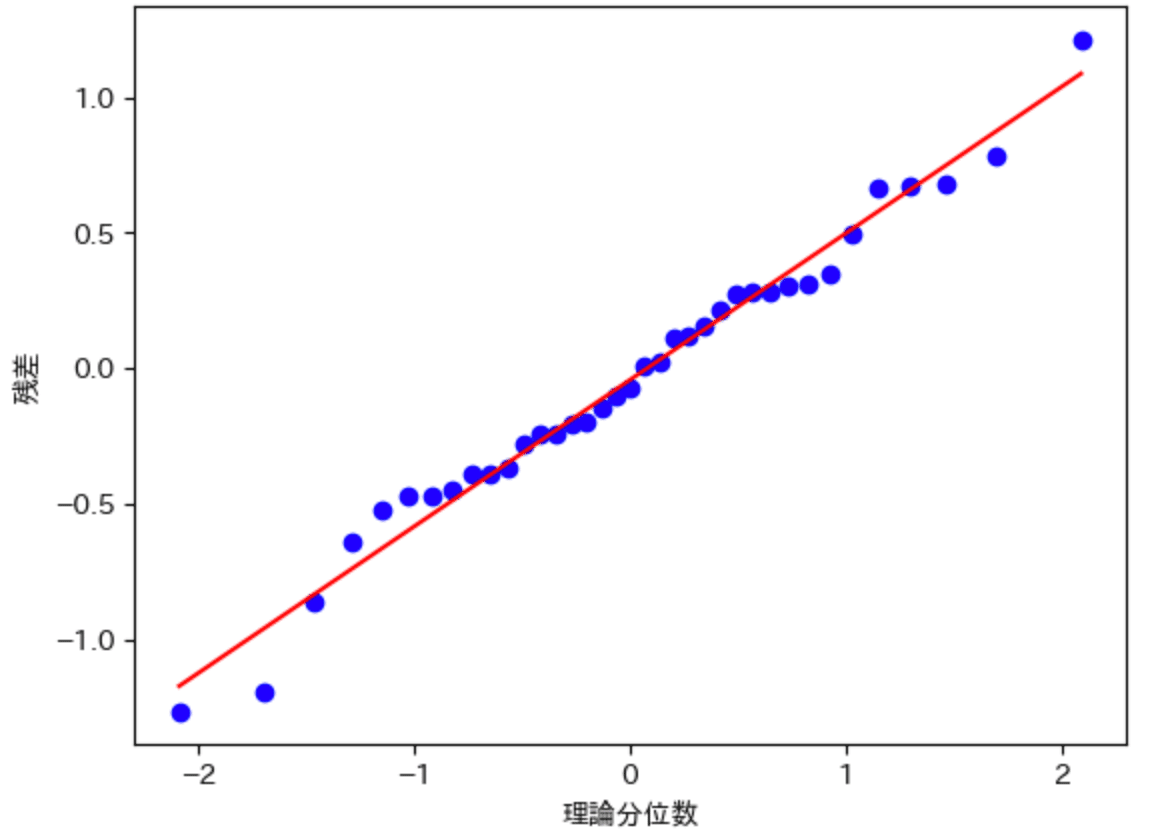
残差の等分散性や正規性については良さそうです。
モデル構築前にトレーニングデータとテストデータに事前に分けていたのでテストデータでのモデル評価もしたいと思います。評価方法は平均二乗誤差(MSE)としています。
結果はこんな感じです。
# 平均二乗誤差(Mean Squared Error, MSE)を計算
mse = mean_squared_error(df['家賃'], df['y_p'])
print(f"平均二乗誤差(MSE): {mse}")
平均二乗誤差(MSE): 0.29137793176366344家賃の単位は、万円です。
コスパのいい物件
score =予測価格 -実際の賃料 の値が大きくなればそれだけコスパがいいことになります。
score順に物件を並べてみたいと思います。
df= df.sort_values(by='score', ascending=False)
df.to_csv('Allscore.csv', index=False)
df['物件名']
1 八広イーストビレッジ
2 ヴェルト西大島グラーセ
3 京成本線 京成小岩駅 3階建 築8年
4 ノースロック
... 上の順位から物件を色々と見ていきました。
でもちょっと違うなー
という部屋も多かったです。内装が好みと違ったり、日当たり悪そうだったりと。
それに今回は、最寄りの駅が何駅なのかを考慮せず
最寄り駅からの距離のみを変数として扱っていたので決していいモデルとは言えません。
最寄り駅ごとにコスパ度を調整できたり、内装が好みか画像で分析できたらいい感じになりそう。
どうすればいいのか今は思いつきません。
現時点での結論
自分の目で部屋を確認して選ぶべきかなと笑
分析結果は参考にしつつも、自分がどの項目を重視するのは人それぞれなので自分の頭で比較検討するのが良さそう。
身も蓋もない結論になりました。
この記事が気に入ったらサポートをしてみませんか?
