Well-tempered metadynamicsについて
ゴール
well-tempered metadynamicsにおけるbias potential V(s,t)と平均力ポテンシャルF(s)の関係式が以下となることを理解することを目的にしています。

参考文献2の式変形を意味を理解しながら追ってみました。解説というより自分の理解のためのノートといった位置づけですが,他の方の参考になるかもという思いで公開しています。
そもそもmetadynamicsとは?
metadynamicsは,系のconfigurational degrees of freedom(空間座標に関する自由度)から構成される自由度にbias potentialを課すことによって,その自由度の平均力ポテンシャルを求めたり系全体のサンプリング効率を向上させる手法に一つです。bias potentialはon-the-flyで累積的に課されていきます。累積加算を続けていくと対象の自由度に関して全ての状態が平等に不安定になるため,bias potentialから逆算して平均力ポテンシャルが得られたり,また不安定にあることによってサンプリング効率が上昇する効果が得られるといった感じです。この手のお話は文章にすると難しくなりがちなので,↓のような動画の方が何をやっているかが分かりやすいと思います。
well-temperedではないmetadynamicsでは,高さ一定のGauss型のbias potentialが課されていきます。
ではwell-tempered metadynamicsとは?
well-tempered metadynamicsではbias potentialの高さが自身の大きさに依存して(小さくなるよう)スケールされます。参考文献2の表式に倣うと,n stepからn+1 stepでbias potentialは以下のように更新されます。

本題
以下の式展開ではbias potentialのs空間における平均,及び平均からの差分をベースに行います。
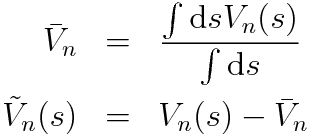
上式のn+1 stepの更新は
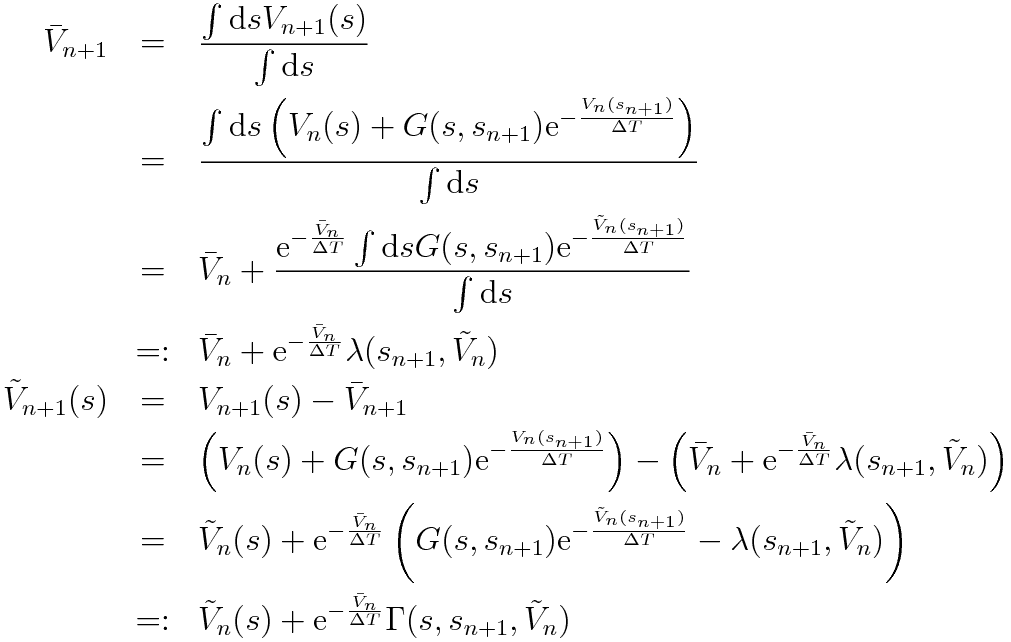
となります。
λの被積分関数が有界である場合,λも有界になります。これは現実的に尤もな仮定なので認めることにします。
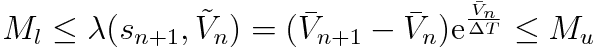
下記の漸近関係

を用いると,

のような不等式も存在すると言えます。このことから,タイムスケールτ

を定義すると,τはシミュレーションが進めば進むほど遅くなる性質を持ちます。
τからτ+dτにおけるbias potentialの変化を考えます。系の平衡化に対してbias potential変化が充分に遅くなる程度にシミュレーションが進んだ段階では,sの取る値はボルツマン分布に従うと仮定できます。また,dτ進むのに多くの実stepが必要になるため,有限和を積分に書換えると,

が成立します。つまり,充分に進んだ段階でのτ時間スケールにおけるbias potentialの変化率は

と表すことができます。
τ→∞の極限ではbias potentialの変化率は0に収束することが期待されるので,

が成立します。ガウス関数はwidth δが充分に小さければ,左辺の積分の値はs'=s付近の値のみが寄与すると見なせるため,

となります。以上より,目的の関係式を導出することができました。
最後に,下記2つの確率分布のKLダイバージェンスを考えることによって収束性を議論します。

便宜上,各確率分布の規格化因子を
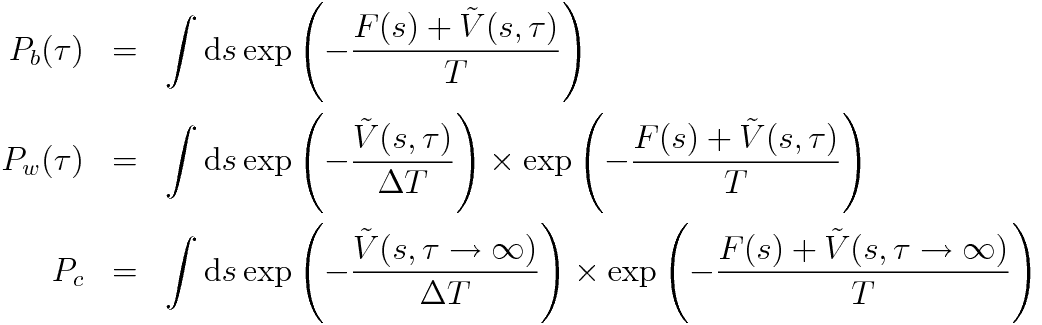
と定義しておきます。
KLダイバージェンスをτに関して微分すると,

となります。

より,


まとめると,
![]()
となります。つまり,τの進み具合が充分遅くなる程度にシミュレーションが進んだ段階では,KLダイバージェンスはτの増加に対して単調に減少します。
参考文献
1. Alessandro Barducci et al, Phys. Rev. Lett. 100, 020603
2. James F. Dama et al, Phys. Rev. Lett. 112, 240602
