ポアソン和公式
ポアソン和公式の勉強をしたので,内容をシェアしたいと思います。ポアソン和公式とは,関数f(x)とそのフーリエ変換の無限級数和に

が成立することを主張するものです。周期関数及びそのフーリエ級数に対しても同様の式が成立します。式の表現や記号はWikipediaの内容に揃えています。Wikipediaの式を少し拡張した,

について,式変形を説明できればと思います。
上式の左辺にフーリエ変換の表式を代入すると,
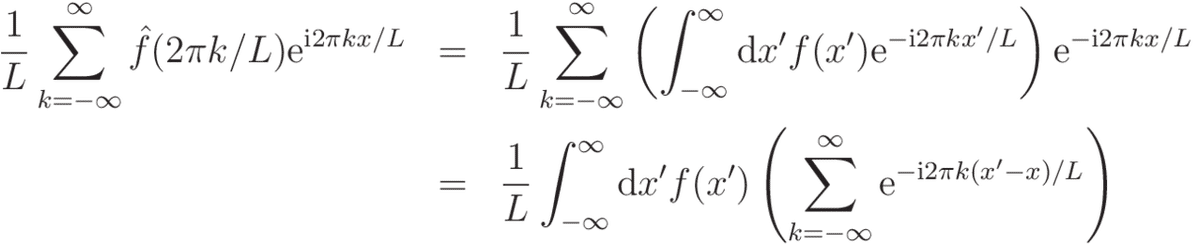
ここで唐突ですが,

を導入します。g(x)は周期Lの周期関数の性質を持ちます。
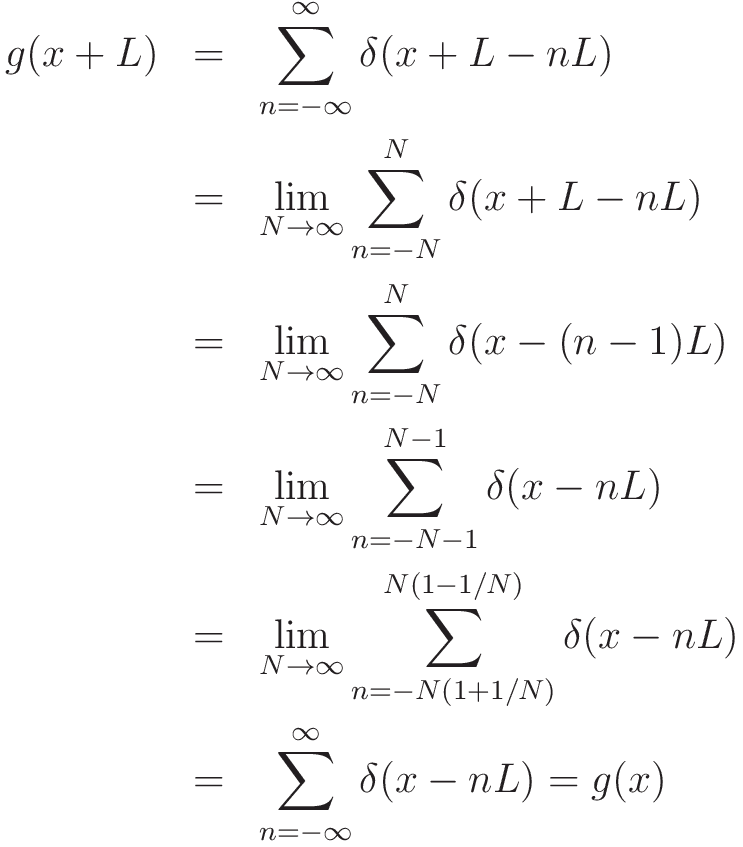
g(x)は周期関数なので,フーリエ級数展開することができます。

つまり,

となることが分かります。この関係式を用いると,

が得られます。以上より,目的に関係式を導くことができました。
この記事が気に入ったらサポートをしてみませんか?
