
r^-αの3次元フーリエ変換
0 < α < 3において,r^-αの3次元フーリエ変換が

と表現できることを示します。
極座標の採用
まず積分変数を極座標にすると,

と式変形することができます。
ガンマ関数とx^{1-α}の関係
次に,ガンマ関数

とx^{1-α}を関連付けます。
1 < α < 3の場合,ガンマ関数のxにα-1を代入し,更にt=xsと変数変換すると,

なる関係式が得られます。
1 < α < 3の場合
ガンマ関数とx^{1-α}の関係式を積分に代入すると

が得られます。
最後の部分の式変形は,参考文献1から
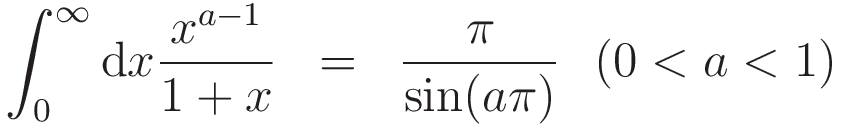
が成立することを利用しました。
ガンマ関数と三角関数の間に

が成立するため,

となります。
更にガンマ関数の倍数公式を用いると

なる関係式が得られるため,

となります。
以上をまとめると,
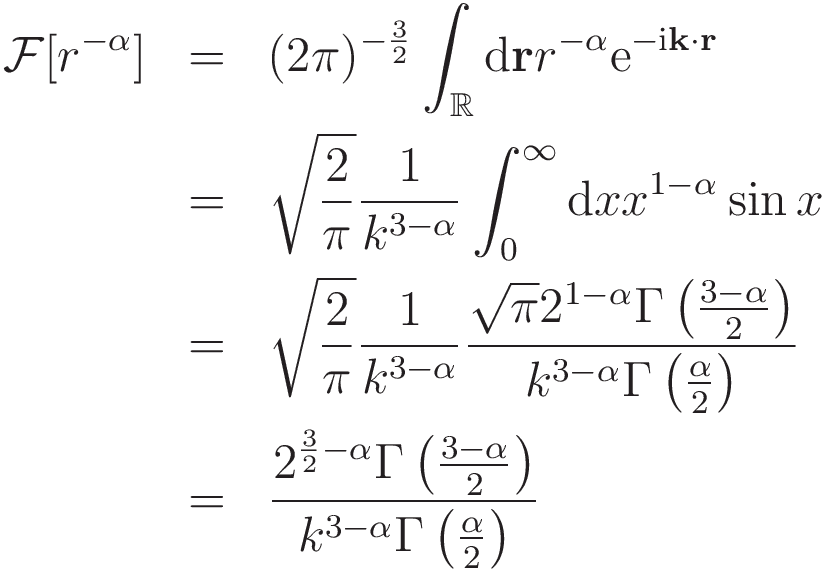
となり,1 < α < 3に対して目的の表式を得ることができました。
0 < α < 1の場合
1 < α < 3の場合と少し異なりますが,似たような式変形をしていくと,

と同じ表式にたどり着きます。
α = 1の場合
α = 1の場合,

となります。
以上より,0 < α < 3において目的の表式を得ることができました。
