
窓際族はクリスマスに億り人の夢を見る~マケデコアドカレ2023~
(2023/12/21追記)2009年開始のシミュレーション結果を追加
これは何の記事?
こんにちは。のんびりテックと申します。
この記事では単純なトレードルールで以下の資産曲線を作っていきます。

本業はリモートワークの窓際族として、AIやデータ分析に携わっていたりいなかったりしてます。しかし、金融の知識には疎いので、その点はご了承ください。
窓際族の矜持とトレード
さて、私はプロの窓際族なので
どうやったら手を抜いて、かつ、安全に利益をあげることができるか
を日々考えています。
トレードの文脈では
「たまにトレードして&リスク最小化して億り人になれるか」
を全力で考えているわけです。
で、どうやってトレードするの?
この記事ではシンプルで再現性のある投資法、
ポートフォリオのリバランス
で実験していきます。
あえて機械学習は使いません。
リバランスはすでに様々なところで推奨されているものの、具体的なシミュレーション結果は少ないように思うので、この記事ではいろいろトライしてみようと思います。また最後に開発アイデアについても記載していきたいと思います。
なお、2024年から始まる新NISAでは
「売却した商品の取得価額分が新たな投資に利用可能となる」ため、
リバランスは相性のよい手法と思われます。枠の再利用に関しては、例えば以下のような書籍が沢山でているので参考にしてください。
ポートフォリオのリバランスについて
さてリバランスのルールは至ってシンプルです。
投資対象の銘柄を選定する
投資ポートフォリオを構築する際の最初のステップです。ここでは、株式、債券、不動産など、多様な資産クラスから特定の銘柄や資産を選びます。
ここが1番のポイントやな。
各銘柄の投資比率を決めて、各銘柄を売買
このステップでは、投資対象とした各銘柄にどの程度の資金を割り当てるかを決定します。これは、リスク許容度や投資目標に基づいて行います。その後、決定した比率に基づいて購入(または売却)します。
特定のタイミングで(期間とか何%乖離したとか)で売買して投資比率を戻す
このプロセスは「リバランス」と呼ばれ、ポートフォリオの目標とする資産配分を維持するために行われます。市場の動きにより資産配分が目標から乖離した場合、特定のタイミング(例えば、定期的にまたは特定の乖離率が発生した場合)でポートフォリオを再調整します。
以下ではこのルールでシミュレーションをしていきます
簡単なリバランスシミュレーション1
このリバランスがワークするのは
どういう状況でしょうか?
端的に言うと、各銘柄が逆の動きをするとき(負の相関を持つとき)です。
簡単なシミュレーションをしてみます。
図の(1)にあるブルー線とオレンジ線を株価に見立ててトレードしてみます。
単なる位相の違うサインカーブです。
各比率は1:1に設定、赤い縦線のタイミングでリバランスをしていきます。スタートの資産は100とします。
(1)は単なるサイン波なので、株価で言えばBOX状態にあるわけですが、リバランス結果は(2)個別の利益、と(3)トータル利益に示す通り、単調に利益が積み上がっていくのがわかります。
リバランスにより、
下がった銘柄は買い増し、上がった銘柄は利益確定
をシステマティックにしているわけですね。
リバランスは、裁量投資において、利益確定のタイミングに悩んだり、下落が怖くて買い増しができない方にオススメです。

コードはこちら。ChatGPTで生成して、ちょっと手直ししてます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 初期設定
initial_investment = 100
days = np.arange(0, 100, 1)
# サインカーブの生成(振幅1、オフセット10、周期20)
investment_A = np.sin(2 * np.pi * days / 20) * 1 + 10
investment_B = np.sin(2 * np.pi * days / 20 + np.pi) * 1 + 10
# Pandasを使用してサインカーブの日々の変化率を計算
investment_A_change = pd.Series(investment_A).pct_change(1).fillna(0).to_numpy()
investment_B_change = pd.Series(investment_B).pct_change(1).fillna(0).to_numpy()
# リバランスの頻度と開始日を設定
rebalance_frequency = 10
rebalance_start_day = 5
# 資産の価値と各投資額の追跡リスト
total_value = []
investment_A_amounts = []
investment_B_amounts = []
# 初期投資額の設定
investment_A_amount = initial_investment / 2
investment_B_amount = initial_investment / 2
# シミュレーションの実行
for day in range(len(days)):
investment_A_amount = investment_A_amount * (1 + investment_A_change[day])
investment_B_amount = investment_B_amount * (1 + investment_B_change[day])
total = investment_A_amount + investment_B_amount
total_value.append(total)
investment_A_amounts.append(investment_A_amount)
investment_B_amounts.append(investment_B_amount)
# リバランス
if day >= rebalance_start_day and (day - rebalance_start_day) % rebalance_frequency == 0:
half_total = total / 2
investment_A_amount = half_total
investment_B_amount = half_total
# 結果のプロット
#plt.figure(figsize=(18, 12))
plt.figure(figsize=(9, 6))
# ポートフォリオの総価値
plt.subplot(3, 1, 1)
plt.plot(days, investment_A, label='Investment A - Sine Curve')
plt.plot(days, investment_B, label='Investment B - Sine Curve')
for day in range(rebalance_start_day, len(days), rebalance_frequency):
plt.axvline(x=day, color='red', linestyle='--')
plt.xlabel('Days')
plt.ylabel('Sine Curve Value')
plt.title('(1) Sine Curves for Investment A & B with Rebalance Timing')
plt.legend()
plt.grid(True)
# 投資額AとBの時系列
plt.subplot(3, 1, 2)
plt.plot(days, investment_A_amounts, label='Investment A Amount')
plt.plot(days, investment_B_amounts, label='Investment B Amount')
for day in range(rebalance_start_day, len(days), rebalance_frequency):
plt.axvline(x=day, color='red', linestyle='--')
plt.xlabel('Days')
plt.ylabel('Investment Amount')
plt.title('(2) Investment Amounts A & B Over Time')
plt.legend()
plt.grid(True)
# サインカーブのプロット(リバランスのタイミングを含む)
plt.subplot(3, 1, 3)
plt.plot(days, total_value, label='Total Portfolio Value')
for day in range(rebalance_start_day, len(days), rebalance_frequency):
plt.axvline(x=day, color='red', linestyle='--')
plt.xlabel('Days')
plt.ylabel('Portfolio Value')
plt.title('(3) Portfolio Value with 20-Day Cycle using Pandas')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
簡単なリバランスシミュレーション2
しかしながら、リバランスは利益を平均化してしまうため、実際にはBuy&Holdよりもトータルの利益は落ちます。
例えば、先ほどの青い線のサインカーブに短調増加の要素を足してみます。
このシミュレーションだと、(1)青い線は10から30近くまで、約3倍になっていますが、(3)リバランスの結果は100から200付近までと約2倍程度しか伸びていません。
リバランスはリスク低減できるが、
同時にリターンも減ってしまう可能性があり、
魔法の方法ではないということは注意しておきましょう。

とある米国株を積み立てシミュレーション
では株のシミュレーションをしていきます。
まず、とある米国のIT銘柄(銘柄Aとします)
をベースに考えていきます。
この銘柄、2000年時点を1としてプロットしていますが、250倍になってますね。

この銘柄に対して、
以下の条件でトレードのシミュレーションしてみます。
ベースラインとしてここでは単なる積立投資をシミュレーションしてみます。
手数料は無視(夢を見たいので)
初期資産を1としてスタート
20営業日毎に資金を0.1追加して積み立てていく
米国株なのでドルで考えている
yfinanceの調整済み株価(Adj Close)利用。つまり配当は即時再投資。
結果は以下の通りで、最終の利益が4500倍になってますね。
ホンマか。。これ積み立ててるだけで人生よかったんや。。

では、最大ドローダウンはどうでしょうか?
ITバブルが弾けた頃に約70%もあり、
これだけに全力投資しているとメンタルが持たないですね。
これを改善していきましょう。

複数銘柄でリバランス
銘柄Aのドローダウンを押さえることができるように
ポートフォリオの銘柄を選んでいきます。
ここではヒューリスティックに
値動き強い、
かつ、
銘柄A含むポートフォリオ内銘柄全てと相関が可能な限り小さくなるような新規銘柄、
をグリーディに順次追加
して、銘柄を選出してみます。
なお2008年以前のデータを学習データとして利用します。2009年からはフォワード期間です。
すると、こんな銘柄群が選択されました。
銘柄Aよりもさらにチート級の銘柄が選択されましたね。。1000倍。。
みんなお世話になってる銘柄やんな。。

面白いことに、
価格だけを利用したシンプルなロジックにもかかわらず、
選択された銘柄郡のセクターがきれいに分かれています。

そういえば、昔、
スタンフォードから来たインターン生(パパがGS)と
トレードの話で盛り上がったのですが、
「各セクターで1番業績いい株買っとけ」
と言っていたのを思い出しました。
きっといまごろ彼はお金持ちでしょう。
では、これらの銘柄でポートフォリオを組み、
以下の条件でリバランスのシミュレーションしてみます。
「値動きの分散の逆数」に比例して資産配分
手数料は無視(夢を見たいので)
初期資産を1としてスタート
20営業日毎にリバランスし、同時に資金を0.1追加して積み立てていく。
米国株なのでドルで考える。
yfinanceの調整済み株価(Adj Close)利用。つまり配当は再投資。
結果は次の通り。


多少は改善しましたが、まだ2008年、2020年のドローダウンは高いです。
株の買いだけでは限界があるのかもしれませんね。
2009年からのフォワードは以下の通り。25倍になっていますが、ドローダウンがまだ35%もあります。

2009年開始を1として正規化した資産曲線
現金を加えてみる
では、現金(ドル)をリバランス対象に加えてみるとどうでしょうか。
株と現金を半分半分にしてみます。
すると利益は大幅に減ってしまいますが、DDは23%まで下がりました。

このドローダウンだと、まだドキドキしてしまいますね。
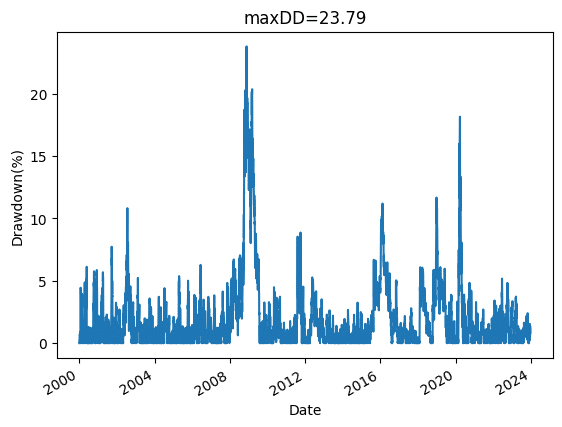
フォワードの2009年からは6.9倍になっています。

2009年開始を1として正規化した資産曲線
謎の金融資産Xを加えてみる
もう少し工夫して、現金の代わりに
米国株と強い負の相関をもつ謎の金融資産X
を追加します。
謎の金融資産Xって何?と思った方は
ぜひいろんなアセットを探索してみてください。
結果は次の通り。かなりドローダウンは減少しました。

これならドキドキも減るよね!

フォワードの2009年からだと、最大DDは12%弱、資産が7倍ぐらいになっています。

2009年開始を1として正規化した資産曲線。
(2023/12/21追記)→→→
上記図は、2000年開始のシミュレーション結果にて2009年を1として正規化した資産曲線です。このため積立の効果が正確に反映されていません(2009年のある程度資産が増えた時点で積み立て0.1しても、その効果は限定的)。
そこで、再度2009年開始の積み立て投資シミュレーションをしてみます。
結果は以下の通り。
積立金額合計は 1 + 0.1*12ヶ月*14年 = 17.8
最終の利益は初期1→50
になっています。
例えば200万円スタートで毎月20万円入金すれば1億に届きますね!

←←←(2023/12/21追記おわり)
やっていることが
「銘柄固定で月1のリバランスと積み立てだけ」
ということを考えると、
最大ドローダウンを12%程度に抑えたこの戦略は
結構イケているのではないでしょうか。
個人的にはこれぐらいのDDだと
安心してトレードできそうです。
のんびり運用すれば億り人にはなれそうやな。
クリスマスにいい夢見れたやんな。
さらなる改良のアイデア
改良の余地は沢山あります。
パッと思いつくものを書いていきます。
このあたりはすでに論文がたくさん出ていると思うので、良い論文知っている方はこっそり教えて下さい。
米国株以外のアセットを試す(仮想通貨、コモディティ、国債、為替、日本株など)
仮想通貨は高いリスクと高い潜在的リターンを持ち、コモディティ(例:金、石油)はインフレや通貨リスクに対するヘッジとして機能することがあります。
日本株は、、どうでしょう。私個人では、日本株の長期投資はうまくいきませんでした。。誰かこっそり教えてください。
リバランスのタイミングを動的にする
静的なリバランススケジュール(例えば年に1回)の代わりに、市場の条件やポートフォリオのパフォーマンスに基づいてリバランスのタイミングを調整します。
マルチファクターモデルの利用で銘柄選定
ファクター投資戦略を採用し、サイズ(小型株)、バリュー(割安株)、モメンタム(上昇トレンドにある株)、品質(堅実な財務状態の株)など、さまざまなファクターに基づいて銘柄を選定します。
月足株価をUMAPなどでクラスタリングして銘柄選定する
UMAP(Uniform Manifold Approximation and Projection)は、高次元データの次元削減と可視化に使われる機械学習技術です。これを使用して株価データをクラスタリングすることで、似たような動きをする株式群を特定し、それぞれのクラスタから最も有望な銘柄を選定することができます。これにより、ポートフォリオ内の銘柄間の相関を減らし、リスクの分散を図ることができます。
Optunaを用いて各銘柄の最適なウェイトを探索する
Optunaは、機械学習モデルのハイパーパラメータ最適化に使用されるオープンソースのフレームワークです。この記事では「値動きの分散の逆数」に比例して資産配分しましたが、Optunaを使用してポートフォリオ内の各銘柄に割り当てるべき資金の最適な比率を探索することができます。実際、私自身はOptunaでパラメータ探索して有効フロンティアをプロットし、ストラテジーの良し悪しを判断しています。
UMAPについて、初心者にはこれがわかりやすい。
Optunaについては以下の本が参考になります。
夢は見れたかい?
様々な金融理論はあるものの、
あえてシンプルな設定でリバランスの実験結果をシェアしました。
「ワイでも資産運用できそうやな!」
と思ってもらえれば幸いです。
インデックスや仮想通貨にも適用できるので
ぜひ試してみてください。
機械学習で日々の値動きを予測するのではなく、
機械学習で長期投資に向いている銘柄を発掘する
のは、ひとつの方向性でしょう。
とはいえ、私自身、金融はド素人なので、
金融強強な方は
もっといい方法あるよとか
ぜひツイッターのDMなどでアドバイスをいただけると嬉しいです。
参考図書
リバランスは銘柄選びが肝要です。米国株に興味を持たれた方は、下記のような本が参考になります。また日本の商社への投資についても書かれておりオススメです。
その他、トレードに有用な参考図書は以下にまとめてあるので参考にしてみてください。
免責事項
本記事の内容は一般的な情報提供のみを目的としており、個別の投資勧誘やアドバイスではありません。投資判断は読者の自己責任において行ってください。専門家の意見を求めることをお勧めします。投資にはリスクが伴い、元本が保証されないことを認識してください。過去のパフォーマンスは将来の結果を保証しません。記事の内容は発行時点のものであり、時間と共に変化する可能性があります。本記事およびその内容に関連して生じるいかなる損失や損害に対しても、著者は一切の責任を負いません。
