【統計学】ロジスティック回帰分析について分かりやすく解説します

この記事では、統計や機械学習で広く使用されるロジスティック回帰分析について、分かりやすくご説明します。

この記事の後半では、エクセルを使ってロジスティック回帰を実際にやってみますので、ぜひ、試してみてください。

✅回帰分析とは

ロジスティック回帰分析の話に入るまえに、そもそも、回帰分析とは？について触れていきます。

回帰分析とは、ざっくり言って、変数X（説明変数といいます）を使って、別の変数Y（目的変数）を予測する手法です。

おそらく、統計的分析手法の中で一番、よく使われているでしょうね。

回帰分析の中でも、最も一般的なのは線形回帰分析です。

説明変数Xと目的変数Yが線形な関係であることを仮定した分析です。

線形回帰分析

ここで、大事な点は、線形回帰分析の場合、予測したい目的変数が量的なデータであるということです。

✅量的なデータと質的なデータについて

ロジスティック回帰を理解するうえで、量的なデータと質的なデータの違いをおさえておくことが重要です。

🎈量的なデータとは

量的なデータとは、数として測定できるものです。身長や体重、年齢、収入などが量的なデータです。数に意味があるものです。

🎈質的なデータとは

質的なデータとは、分類（カテゴリー）として測定できるものです。性別や血液型、満足度などが質的データです。数に意味がないものです。

✅ロジスティック回帰分析とは

さて、本題のロジスティック回帰分析です。

世の中のデータのすべてが線形的な関係にあるわけではありません。非線形な関係にあるデータも多く存在します。

また、予測したい目的変数が量的なデータではなく、質的なデータであるケースもあります。

こうした時に使われるのがロジスティック回帰分析です。

🎈事例

具体的な事例で見ていきましょう。

模擬テストの点数から、試験の合格率を予測することを考えます。

ここに、20人分の模擬テストの点数と、試験結果のデータ（合格は1、不合格は0）を用意しました。

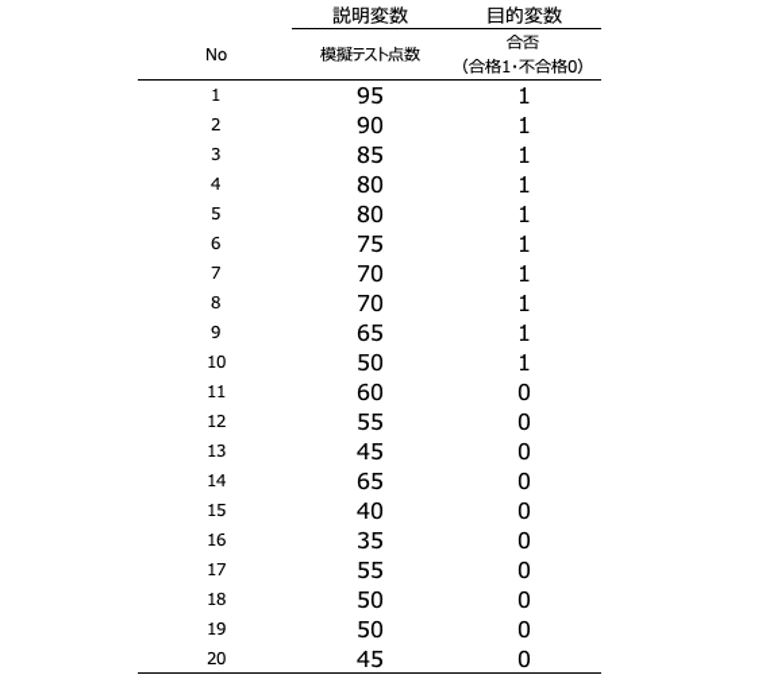
このデータをグラフにすると以下のようになります。

X軸は模擬テストの点数です。35点〜95点までありますね。
Y軸は試験結果です。1と0しかありません。

これに回帰直線をあてると以下のようになります。

当てはまりがよくないですね。
しかも、合格率は0〜1までの値しかとらないのに、マイナス値や、1より大きい値もとれてしまって、予測モデルとしては不適当です。

こうしたケースで、予測モデルに適したのがロジスティック回帰分析です。

ロジスティック回帰分析は、ある事象（ここでは合格・不合格）を直接予測するのではなく、ある事象が発生する確率を予測します。つまり、合格率を予測します。

事例でロジスティック回帰分析を実行すると、以下のようなS字型の曲線が得られます。
線形ではなく、非線形でXとYの関係を捉えるのがポイントです。

ロジスティック回帰分析

当てはまりも良さそうですし、目的変数は0〜1の間に入っています。

この分析の解釈として、予測確率が0.5を超えれば合格、0.5以下であれば不合格と言うこともできそうです。

✅実際にロジスティック回帰分析をやってみよう

エクセルを使ってロジスティック回帰をやってみましょう。

1️⃣ステップ1

模擬テストの点数と合否のデータに、定数項、予測確率、対数尤度の列を追加し、計算式を入力します。また、対数尤度の合計×-2を計算するセルを用意します。

定数項と模擬テストの点数の係数は、一旦、0で置いておきます。

模擬テスト点数をX、Xの係数をα、定数項をβとしたとき、予測確率Yは以下の計算式になります。

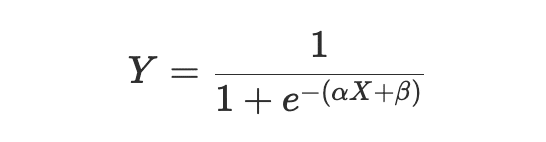
eはネイピア数（自然体数）です。

この計算式は、ロジスティックシグモイド関数と呼ばれています。
線形回帰の場合、Y=αX＋βになるところです。

この時点では、αとβが0になっているため、予測確率は全て0.5になります。

2️⃣ステップ2

ここから、対数尤度の合計×-2の値が最小になるようなαとβを計算します。
そのためにエクセルのソルバー機能を使います。

3️⃣ステップ3

ソルバー機能を使うと、係数が変わり、予測確率が更新されます

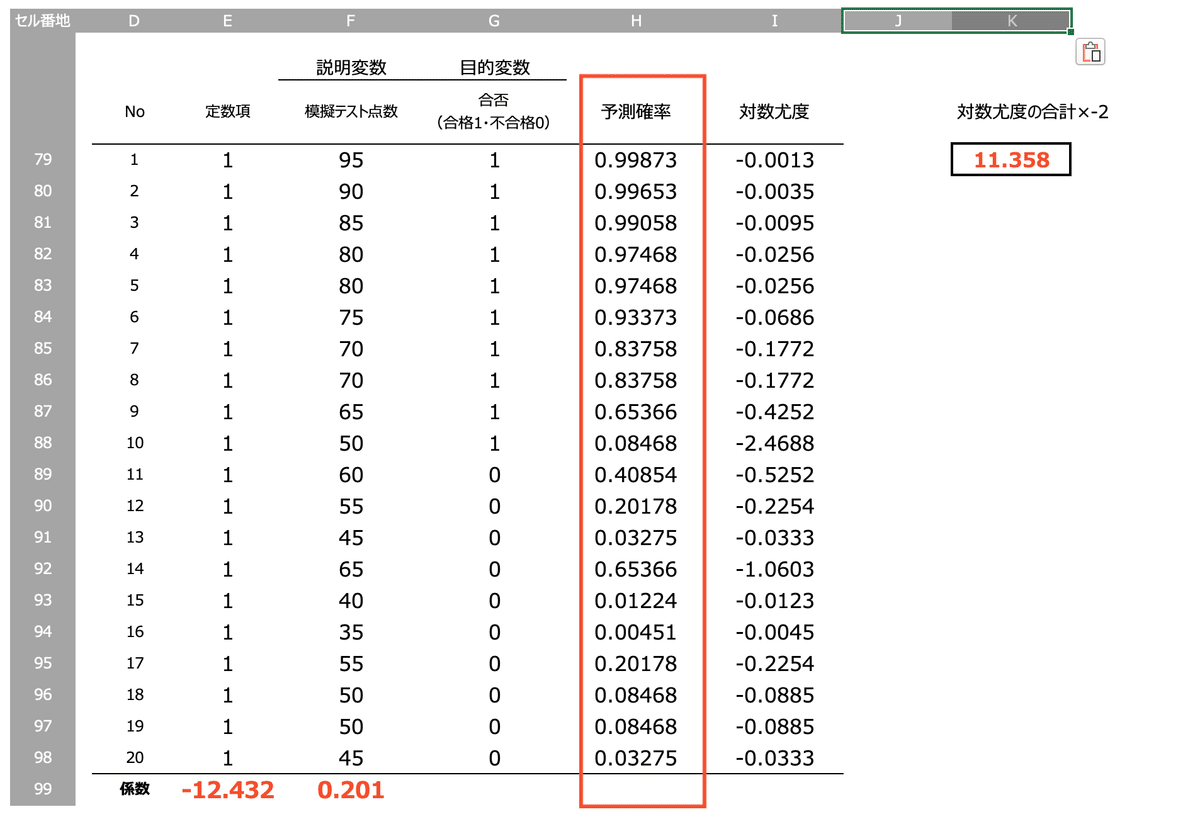
これにより、予測確率の計算式は以下のようになりました。

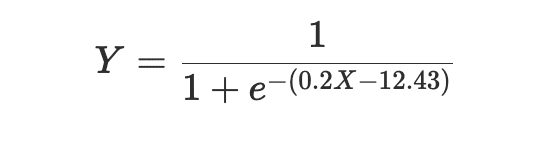
✅線形回帰チックにやってみる

さきほどの予測確率の式は、Yの部分を少し変形することで、線形回帰分析と同じように表すことができます。

これをロジット変換と呼びます。

ロジスティック回帰の場合は、予測確率Yは0〜1の範囲内でしたが、Yをロジット変換することで、左辺の$${logY/(1-Y)}$$は-♾️〜♾️の値をとることができるようになります。

グラフにするとこんな感じ

✅さいごに

統計を勉強するにあたっては実際に手を動かして計算することが大事です。
ぜひ、お手元のデータを使って、いろいろ試してみてください。

なお、今回のロジスティック回帰は一般化線形モデルというカテゴリーに入ります。
伝統的な一般線形モデルとの関係を簡単に図示してみましたので、参考にしてください。