
【機械学習の初学者向け】F1スコアについて理解しよう!
はじめに
機械学習モデルの良し悪しを評価する指標にF1スコアがあります。
機械学習を勉強して初めて知る人も多いと思いますが、
初学者にとっては、分かりにくい指標ではないかと思います。
私自身も初学者の領域ですが、
F1スコアについては、よく分かっていませんでした。
このたび、金融データ活用推進協会が主催する
機械学習コンペ「第2回金融データ活用チャレンジ」に参加したところ、
評価指標が「Mean F1スコア」とのこと!
F1スコアすらも分からないのに、そこにMeanが加わるとは!!
これは学びの良い機会だと考え、
F1スコアについて初歩的なところから学び直しました。
この記事では、
「第2回金融データ活用チャレンジ」での予測データや自分が試したことを踏まえながら
・F1スコアがどういうものか、
・MeanF1スコアとはなにモノか、
・スコアアップを図る方法、など
初学者がF1スコアを理解できるよう、分かりやすく解説していきます。
◾️金融データ活用チャレンジの概要はこちら↓
★まずは、混同行列を理解する
F1スコアを理解する前に
欠かせないのが混同行列です。
まずは、これを正しく理解しましょう。
混同行列とは、
モデルの予測値が陽性か陰性か
実際の値が陽性か陰性か
を表にしたものです。
これらの組み合わせには
以下の❶〜❹の4パターンがあります。

モデルが正しく予測したパターン→頭にT(True)がつく
❶TP(True Positive):モデルが陽性と予測し、実際も陽性だった
❷TN(Ture Negative):モデルが陰性と予測し、実際も陰性だった
モデルが間違って予測したパターン→頭にF(False)がつく
❸FP(False Positive):モデルが陽性と予測し、実際は陰性だった
❹FN(False Negative):モデルが陰性と予測し、実際は陽性だった
つぎからは、混同行列を使って
いくつかの指標について見ていきましょう。
★正解率について理解する
もっともシンプルな正解率について考えます。
具体的な数字を入れて見ていきましょう。

正解率とは、以下の式で表されます。
正しく予測した数値を全体の数値で割ったものになります。
分かりやすい指標ですね。
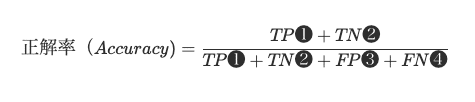
具体的な数値に当てはめると、
正解率=(5+100)÷(5+10+10+100)=0.84
正解率84%、まあまあ高い数値です。
素人感覚ですと、
「モデルの精度として十分じゃね?」となりますが、
そうはなりません。
なぜでしょうか?
このデータは、
実際の陽性の数が15、陰性の数が110と
陰性に偏った不均衡データになります。
125のデータ全てについて、
モデルが陰性と予測した場合でも
正解率を算出すると、
110÷125=88%となってしまいます。
つまり、陽性を正しく予測しなくても
高い正解率が出てしまうのです。
このように、
陽性と陰性の数が不均衡な場合においては、
正解率だけ見ていると
モデルの精度を見誤ります。
そこで大事になってくるのが
これから説明する適合率、再現率になります。
★次に、適合率と再現率を理解する
適合率と再現率は
混同行列の数値を使って計算できます。
どこの行と列を計算しているのか?というと
以下の通りになります。

◾️適合率 Precision
モデルが陽性と判断し、実際に陽性だった割合をいいます。
数式で表すと以下の通りになります。

◾️再現率 Recall
実際に陽性だったもののうち、モデルが陽性と判断した割合をいいます。
数式で表すと以下の通りになります。

適合率と再現率の式は非常に似ていて、
どこが違うかというと、
分母に入っているのが、❸FPか❹FNかということです。
❸FPも❹FNも、いずれも「間違った予測」ですよね。
なので、間違った予測を減らすことで数値は上がります。
つまり、適合率と再現率の違いは、
どんな「間違い」を減らしたいかなんです。
◾️適合率が重視される時
スパムメールの検出モデルを想像してみてください。
スパムメールを陽性、スパムメールでないと陰性とします。
検出の結果、陽性とでたが、実際は陰性だったパターン(❸)と
検出の結果、陰性とでたが、実際は陽性だったパターン(❹)の
どちらを減らしたいでしょうか?
これは❸の方を減らしたいですよね
実際は重要なメール(陰性)なのに、スパムメール(陽性)として検出され読めなくなる場合、業務への影響は大きいでしょう。
逆にこのスパムメールが見逃され手元に届いたとしても、開封しなければいいだけですから、業務への影響は大きくありません。
適合率は誤検出をなくしたい時に重視されます
◾️再現率が重視される時
コロナ検査における陽性・陰性の判定を想像してみてください。
ここでは、予測を検査と読み替えましょう。
検査の結果、陽性とでたが、実際は陰性だったパターン(❸)と
検査の結果、陰性とでたが、実際は陽性だったパターン(❹)の
どちらを減らしたいでしょうか?
この場合は、❹の方を減らしたいですよね。
実際は陽性の患者を陰性として判定してしまう方が、患者本人にとっても、社会的にもリスクが高いからです。
再現率は見逃しをなくしたい時に重視されます。
ちなみに、適合率と再現率はトレードオフの関係にあり、
どちらかを高めようとすると、
どちらかが低くなります。
★そして、F1スコアを理解する
さて、ここからが本丸のF1スコアになります。
F1スコアは、
適合率と再現率のバランスを重視した指標になります。
具体的には、
適合率と再現率の調和平均がF1スコアとなります。

調和平均とは、比率を扱う場合に使われる平均の一種です。
たとえば、異なる速度で同じ距離を移動する場合の
平均速度を求めるのに適しています。
具体的には、各数値の逆数(1をその数値で割ったもの)の平均を取り、
それをさらに逆数に戻すことで計算します。
◾️具体的に計算してみよう!
以下は、第2回金融データ活用チャレンジで、
実際に自分の作ったモデルが算出した
混同行列になります。

さきほどの図とは縦横が逆なので注意です。
Actualが実際、Predictedが予測になります。
また、
陽性1:債務を完済した者
陰性0:債務不履行になった者
になります。
Actualの数を見ると、
陽性1:37,767
陰性0:4,540
とかなりの不均衡データになっています。
なお、混同行列を描画するPythonコードは以下の通りです
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(df["MIS_Status"], df["pred"] >=0.5)
plt.figure(figsize=(5, 5))
sns.heatmap(cm, annot=True, fmt="d", cmap="Blues")
plt.title(f'Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()dfの"MIS_Status"に実際の値、
dfの"pred"にモデルが予測した確率が
格納されているとします。
(次項以降でも同じ前提です)
◾️陽性1に対するF1スコア
多数クラスの陽性1に対してF1を計算してみましょう。
適合率は、37257/(37257+3513)=91.4%
再現率は、37257/(37257+510)=98.6%
F1スコアは、(2*0.914*0.986)/(0.914+0.986)=94.8%
と、かなり高い数値になりました。
めでたし、めでたし….
とはならなかったのです。
★Mean F1スコアとはなんぞや
金融データ活用チャレンジの評価指標は
単純なF1スコアではなく、
MeanF1スコアと呼ばれるものでした。
(別名、マクロF1スコア)
計算式はこうです
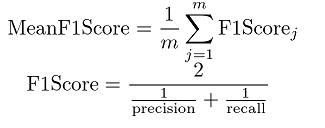
さきほどのF1スコアは、
陽性1(債務を完済した者)というクラスに対してものでした。
しかし、クラスには、
陰性0(債務不履行になった者)というクラスも存在します。
金融のタスクを考えるうえでは、1より0の方が重要そうですよね。
MeanF1スコアは、
こうしたクラスごとのF1スコアを計算し、
それらを平均せよというものでした。
MeanF1スコアを求めるPythonコードは下の通りになります
from sklearn.metrics import f1_score
score = f1_score(df["MIS_Status"], df["pred"] >= 0.5, average = "macro")通常のF1スコアと異なるのは、引数としてaverage="macro"がある点です。
◾️陰性0に対するF1スコア
さきほどの混同行列に基づき、
クラス0についてのF1スコアを計算してみましょう。
適合率は、1027/(1027+510)=66.8%
再現率は、1027/(1027+3513)=22.6%
F1スコアは、(2*0.668*0.226)/(0.668+0.226)=33.8%
となり、めちゃくちゃ低い数値になりました。
クラス0については、特にRecallがうまく計算できていないことが
よく分かりますね。
◾️Mean F1スコア
クラス1とクラス0のF1スコアから
MeanF1スコアを求めると。。。
0.643となりました。
クラス1のF1スコアが高くても、
クラス0のF1スコアが低いとこうなりますよね。
今回のような不均衡データの場合は、
特に数が少ないクラスのF1についても、
よく見ていく必要がありそうです。
★閾値を理解しスコアアップを図る
機械学習のモデルは、陽性である確率を計算します。
確率は0〜1の値をとる連続値です。
F1スコアが評価指標になっている場合には、
その連続値である確率を
陽性1か陰性0かの二値に分けてやる必要があります。
そして、、、
どの確率以上を陽性=1とし、
どの確率未満を陰性=0とするかの分かれ目は、
人間が決める必要があります。
この陽性と陰性の分かれ目となる基準を閾値(Threshold)と呼びます。
一般的に、閾値は0.5とすることが多いです。
先ほどのモデルの予測も、
実は、閾値0.5として計算したものでした。
F1スコアの場合、
閾値の違いでスコアが大きく動くことがありますので、
ちゃんと考える必要があります。
◾️閾値を変えることで何が変わる?
以下は、実際にモデルが計算した
予測値の確率分布になります。
閾値を0.5とするか、0.6とするかで
陽性1の予測数が変わることがわかりますね。

一般的には0.5を閾値とすることが多いですが、
0.5を閾値とすることが必ずしもベストではありません。
陽性クラスの場合、
閾値を0にすれば、
全て陽性判定となるため、再現率は100%になりますが、
閾値が0.5だった場合に比べて、
適合率は下がります。
逆に閾値を1にすれば、
全て陰性判定となるため、陽性クラスの再現率と適合率は
0%になります。
陰性クラスの場合、逆のことが起きますね。
それでは最適な閾値はどうやって求めたら良いのでしょう?
◾️最適な閾値を求めよう!
閾値を細かく動かすことで、
MeanF1スコアが最大となる閾値を
解析的に求めるのが手っ取り早いです。
具体的には、
閾値を0→1に向かって0.001ずつ上げ、
閾値ごとのMeanF1スコアを計算して、
どの閾値の時にMeanF1スコアが最大になるかを計算します。
こういうことはPythonが得意です。
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import f1_score
# 実際の値と予測値を設定
y_true = df['MIS_Status']
y_scores = df['pred']
# 閾値のリストを生成
thresholds = np.arange(0, 1.001, 0.001)
# 各閾値でのF1スコアを計算
f1_scores = []
for v in thresholds:
score = f1_score(y_true, y_scores >= v, average='macro')
f1_scores.append(score)
# F1スコアが最大の場合の閾値を見つける
best_score = max(f1_scores)
best_v = thresholds[f1_scores.index(best_score)]
# F1スコアを閾値に対してプロット
plt.figure(figsize=(8, 6))
plt.plot(thresholds, f1_scores, label='Mean F1 Score')
plt.xlabel('Threshold')
plt.ylabel('Mean F1 Score')
plt.title('Mean F1 Score by Threshold')
plt.axvline(x=best_v, color='red', linestyle='--', label=f'Best Threshold = {best_v}')
plt.legend()
plt.grid(True)
plt.show()
print(f"Best Mean F1 Score: {best_score}, Best Threshold: {best_v}")
Best Mean F1 Score: 0.677
Best Threshold: 0.761
とでました。
MeanF1スコアが
閾値0.5の場合、0.643でしたが、
閾値を調整した場合、0.677まで上がりました!!
これを可視化すると以下のグラフの通りになります
このグラフからも、閾値を調整すると
MeanF1スコアが変わることがわかると思います。

さいごに
機械学習コンペにおいては、
与えられた評価指標の性質を理解し、
評価指標に合わせてモデルの予測値を最適化していくことが
重要だと思います。
この記事を通して、
機械学習初学者の方のF1スコアへの理解が
少しでも深まればと思います。
私自身、昨年開催された第1回金融データ活用チャレンジに続いての
2回目の参加でしたが、今回も大いに勉強になり、
機械学習のスキルが格段にアップしたことを実感しています。
来年もぜひ参加したいです!!
ちなみに、第1回の参加感想は↓
いいなと思ったら応援しよう!

