形而下学の概念を計算してPython化

2025年1月25日 23:40

**形而下学（Metaphysics Below）**の概念は、物理的で観測可能な事物や現象に焦点を当てた哲学的思考を扱います。これは「形而上学」（存在や本質を扱う）と対比されるもので、具体的で物質的な世界における実体や因果関係を考察します。

形而下学の要素をPythonでモデル化するためには、以下の基本構造を取り入れます。

形而下学のモデル

物質（Entity）:
- 存在する具体的なもの（物体、エネルギー、現象）。
属性（Attributes）:
- 物質の特性や性質（例: 質量、速度、形状）。
相互作用（Interaction）:
- 物質同士の因果関係や影響。
時間と空間（Time and Space）:
- 存在が展開する次元。

Pythonコード: 形而下学のモデル化

class Entity:
    def __init__(self, name, attributes):
        """
        物質の基本単位を表現するクラス
        :param name: 存在の名前
        :param attributes: 存在の属性（辞書形式）
        """
        self.name = name
        self.attributes = attributes

    def interact(self, other):
        """
        他の物質と相互作用をシミュレート
        :param other: 相互作用する対象
        :return: 相互作用の結果
        """
        print(f"{self.name} と {other.name} が相互作用しました。")
        interaction_result = {}
        for attr, value in self.attributes.items():
            if attr in other.attributes:
                # 属性の相互作用（例: 質量の合計、速度の比較など）
                interaction_result[attr] = value + other.attributes[attr]
        return interaction_result

    def display(self):
        """
        物質の属性を表示
        """
        print(f"{self.name} の属性: {self.attributes}")


# 形而下学の物質例
entity1 = Entity(name="物体A", attributes={"mass": 10, "velocity": 5})
entity2 = Entity(name="物体B", attributes={"mass": 15, "velocity": -3})

# 属性の表示
entity1.display()
entity2.display()

# 相互作用のシミュレーション
result = entity1.interact(entity2)
print(f"相互作用の結果: {result}")

コードの説明

Entity クラス:
- 存在する物質のモデル。
- 名前（name）と属性（attributes）を持つ。
相互作用のシミュレーション:
- 属性（例: 質量や速度）同士の相互作用を計算。
属性の表示:
- 物質の属性を可視化。
出力例:

物体A の属性: {'mass': 10, 'velocity': 5}
物体B の属性: {'mass': 15, 'velocity': -3}
物体A と 物体B が相互作用しました。
相互作用の結果: {'mass': 25, 'velocity': 2}

拡張: 具体的な形而下学的モデルの例

1. 運動エネルギーの計算

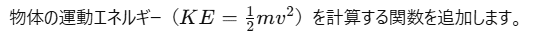
def calculate_kinetic_energy(entity):
    """
    運動エネルギーを計算
    :param entity: 対象の物質
    :return: 運動エネルギーの値
    """
    mass = entity.attributes.get("mass", 0)
    velocity = entity.attributes.get("velocity", 0)
    return 0.5 * mass * velocity**2

# 運動エネルギーの計算
ke1 = calculate_kinetic_energy(entity1)
ke2 = calculate_kinetic_energy(entity2)

print(f"{entity1.name} の運動エネルギー: {ke1}")
print(f"{entity2.name} の運動エネルギー: {ke2}")

出力例:

物体A の運動エネルギー: 125.0
物体B の運動エネルギー: 67.5

2. 時間進行による位置の変化

物体が一定速度で移動するときの位置を時間進行とともに計算します。

def update_position(entity, time):
    """
    時間進行による位置の変化を計算
    :param entity: 対象の物質
    :param time: 経過時間（秒）
    :return: 新しい位置
    """
    velocity = entity.attributes.get("velocity", 0)
    initial_position = entity.attributes.get("position", 0)
    new_position = initial_position + velocity * time
    return new_position

# 初期位置を設定
entity1.attributes["position"] = 0
entity2.attributes["position"] = 10

# 位置の更新
time_elapsed = 3  # 3秒経過
position1 = update_position(entity1, time_elapsed)
position2 = update_position(entity2, time_elapsed)

print(f"{entity1.name} の新しい位置: {position1}")
print(f"{entity2.name} の新しい位置: {position2}")