深層学習day1~day2(ラビットチャレンジ)
全体像
・識別モデル
・確認テスト
⇒ 複数層からなるNNでの多数のパラメータ、活性化関数の組み合わせにより、入力から出力を計算するモデルを作成すること。
③重みと④バイアスの最適化により、それを達成する。

・確認テスト


・一般的に4層以上が深層学習と言われている
入力層~中間層
・入力に重みをかけてバイアスを足し合わせ、活性化関数をかけて中間層を作り出す。
・確認テスト
⇒ x1 : 体長
x2 : 体重
x3 : 足の大きさ(面積)
x4 : 足の長さ
・確認テスト

⇒ u = np.dot(x, W) + b
・確認テスト

⇒ 回答

活性化関数
・確認テスト

⇒ 解答

・入力に重みをかけて、バイアスを足したものに適用するもの
・中間層用の活性化関数
- ReLU関数
> 今、最も使われている
> 勾配消失問題の回避とスパースかに貢献して、良い結果をもたらす
- シグモイド(ロジスティック)関数
> 大きな値では出力変化が微小なため、勾配消失問題を引き起こすことがあった。
- ステップ関数
> 今は使われていない
・出力層用の活性化関数
- ソフトマックス関数
- 恒等写像
- シグモイド(ロジスティック)関数
・確認テスト

⇒ 解答

出力層
・人間が欲しい結果(確率)を出す役割
・訓練データ(正解)との差から、誤差関数を用いて、誤差を計算する
・確認テスト

⇒ 解答
- 二乗しない場合、正の誤差と負の誤差が打ち消しあう可能性があり、訓練データとの差を正しく表現できないから。
- パラメータを更新する際に、誤差関数を微分する必要があり、その際の計算を簡単にするため。
・分類問題の場合、誤差関数にはクロスエントロピー誤差を用いる
・出力層では信号の大きさはそのままに変換
・分類問題では出力は0~1の範囲かつ総和が1となる
・回帰に用いる出力層
> 恒等写像
> 二乗誤差
・二値分類に用いる出力層
> シグモイド関数
> 交差エントロピー
・多クラス分類に用いる出力層
> ソフトマックス関数
> 交差エントロピー
・確認テスト

⇒ 解答
①はソフトマックス関数を通した後の出力
②/③はそのクラスに属する確率

・確認テスト

⇒ 解答
- ①で誤差関数にクロスエントロピーを指定
- ②でクロスエントロピー誤差を計算

勾配降下法
勾配降下法
・勾配降下法を利用してパラメータを最適化する
・確認テスト

⇒ 解答

・学習率
- 非常に大きい ⇒ 最小値にたどり着かずに発散
- 非常に小さい ⇒ 収束するまでに時間がかかる、局所最適に陥る
・出力値と訓練データの誤差から訓練データを1回更新するサイクルをエポックという
確率的勾配法
・学習に使う全データから、一部のデータだけを使って学習を進めていく。
・無駄な計算を減らせる
・局所最適に収まりづらい
・オンライン学習が可能
- バッチ学習 : 最初に全データを準備する必要あり、勾配降下法はこちら。
- オンライン学習 : モデルに都度都度データを与えて、学習していく、最初にデータを全て準備する必要がない
・確認テスト
⇒ 最初にすべてのデータを準備するのではなく、その都度データを与えて学習させていく方法。メモリを大量に使用しなくて済む
ミニバッチ勾配降下法
・例えば1万枚の画像を256枚ずつとかに分けて学習させていく方法
・確率的勾配法のメリットはそのままで、計算機の計算資源を有効活用できる
- CPUを利用したスレッド並列化
- GPUを利用したSIMD(Single Instruction Multi Data)並列化
・ミニバッチ毎で並列で計算
・現在の計算機で1つができる処理速度は限界に達している
⇒ 同時並行でたくさんのことをやるしかない
・確認テスト

・解答
⇒

誤差逆伝搬法
・誤差勾配の計算
- 数値微分
> 計算量が多くなり、負荷が大きい
⇒ 誤差逆伝搬法を利用する
・誤差からの微分の逆算することで、不要な再帰的計算を避けることができる
・微分の連鎖率を利用している
・確認テスト

⇒ 解答

・確認テスト

⇒ 解答

勾配消失問題
・中間層が増えた場合、誤差情報がどんどん小さくなっていき、勾配が緩やかになることによって、パラメータの更新がなされず、最適解に到達できないという問題
・シグモイド関数は微分値が最大でも0.25にしかならず、それを何層にもわたってかけ合わせていくと、誤差情報がほとんどゼロになってしまう。
・確認テスト

⇒ 解答 (2)
勾配消失問題の解決方法
・活性化関数の選択
- ReLU関数
> 微分値は0未満では0、1以上では1
> 役に立つときはそのまま、役に立たないときは0となる
必要な情報だけを取り出すことができる
⇒ スパース化
・重みの初期値設定
- 乱数を使って初期値を設定する
> 平均が0で分散が1(標準正規分布、自然界に一番多い)がよく使われていたが、勾配消失問題が発生
> 重みの値が0か1に寄ってしまう
- Xavier
> 重みの要素を前の層のノード数の平方根で割る
> ReLU関数、シグモイド関数、双曲線正接関数(tanh)に適用化
> 重みがいい感じにばらつく
- He
> Xavierに√2をかける
・確認テスト

⇒ 重みの更新後の値が類似してしまい、モデルの表現力が低下して、適切なモデルにならなくなる
・バッチ正規化
- ミニバッチ単位で、入力値のデータの偏りを抑制する手法
- 活性化関数に値を渡す前後に、バッチ正規化の処理を挟む
- メリット
> 中間層の重みの更新が安定化(学習がスキルアップする、早くモデルが仕上がる)
> 過学習を抑えられる
・確認テスト

⇒ 解答
- 中間層の重みの更新が安定化し、学習が速くなる
- 過学習が抑えられる
学習率最適化手法
勾配降下法

・学習率によって、発散したり、収束が遅くなったり、局所最適に陥ったりする
⇒ 以下の指針に基づき、学習率最適化手法を利用して学習率を最適化
> 初期の学習率を大きく設定して、徐々に学習率を小さくする
> パラメータ毎に学習率を可変させる
モメンタム
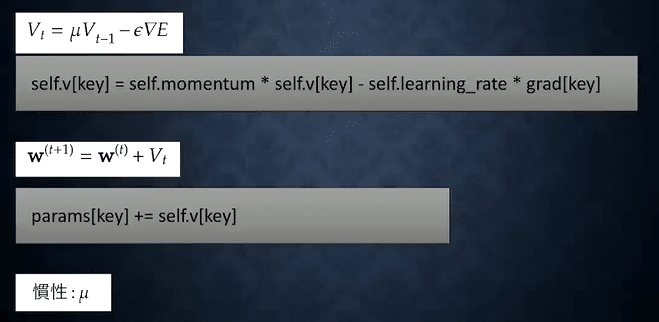
・大域的最適解に到達しやすい
・動き続けてピタッと止まらない
Adagrad
・勾配の緩やかな斜面に対して、最適解に近づける(緩やかな斜面に強い)
・学習率が徐々に小さくなるので、鞍点問題を引き起こすことがある

RMSProp
・局所最適解にはならず、大域的最適解となる。
・ハイパーパラメータの調整が必要な場合が少ない

Adam
・モメンタムとRMSPropのメリットを組み合わせたアルゴリズム
- モメンタムは進みが良い方向に一気に進む
> 動いたら動き続けたくなって、なかなか収束しない
- AdagradやRMSPropはそれまでの学習率の経験をうまく生かす
・鞍点を抜ける能力が高い
・振動していると、学習が上手くいっているかどうかの見分けがつきづらい
過学習
全体像
・テスト誤差と訓練誤差とで学習曲線が乖離すること
・原因
- パラメータの数が多い、
- パラメータの値が適切でない
- 入力値が少ないのにニューラルネットワークの大きさが大きい時、過学習が起きやすい
> 小さな入力には、小さなNNを用いるべき
- 自由度が高すぎる
- 重みが極端に大きい値になっている
> 重要な場所の重みは大きくなっている
> 過大評価されている場合、一部の入力データに対して極端な反応となっている
⇒ 極端にならないように、制約をつけてあげる(正則化)
正則化
・ネットワークの自由度(層数、ノード数、パラメータの値etc...)を制約すること
・Weight Decay(荷重減衰)
・誤差に対して正則化項を加算することで重みを抑制する
- 過学習が発生しそうな重みの大きさ以下に制限しながら、極端にならないように重みの大きさにばらつきを出すことが解決策
・誤差関数にpノルムを加える
・λはハイパーパラメータ
・L1正則化(Lasso回帰、L1ノルム)
- マンハッタン距離
- スパース
> モデルが効率的になって、不必要な部分がそぎ落とされる
・L2正則化(Ridge回帰)
- ユークリッド距離
- スパースでない

・確認テスト

⇒ 解答 : 右側
・ドロップアウト
- ランダムにノードを削除して学習させること
- データのバリエーションが多い程、過学習が起きづらくなる
> データ量を変化させずに、異なるモデルを学習させていると解釈できる
畳み込みニューラルネットワークの概念
CNNの全体像
・画像の識別や処理によく用いられる
・次元間でつながりのあるデータを扱える(画像、音声、動画等)
・CNNの処理は畳み込みニューラルネットワーク
・LeNet
- Input : 32 x 32 (= 1024)
- Convolutions : 28 x 28 x 6 (= 4704)
- Subsampling(要約) : 14 x 14 x 6(= 1176)
- Convolutions : 10 x 10 x 16 (= 1600)
- Subsampling(要約) : 5 x 5 x 6(= 400)
- Full Connection : 120
- Full Connection : 84
- Output : 10種類
・出力の数はフィルターの数
・全結合層手前までが、次元のつながりを持ち、特徴量を抽出する部分
・全結合層の部分が人間が欲しい結果
畳み込み層
・3次元の空間情報も学習できるような層
・入力画像に対してフィルター(重み)とバイアスを付加する
・フィルターを通すと元の画像よりも小さくなってしまう
⇒ パディングを用いる
パディング
・元の画像の周りをゼロや一番近い場所の数字等で埋めて、その後にフィルターを通すことで、画像サイズが小さくなることを防ぐ
ストライド
・フィルターを動かす量のこと
チャンネル
・フィルターの数のこと
プーリング層
・畳み込み演算と似ているが、重みを使わずに処理をする
・Max Pooling
- 対象領域のMax値を取得
・Average Pooling
- 対象領域の平均値を取得
・確認テスト

⇒ 解答 : 7 x 7
最新のCNN
AlexNet
・5層の畳み込み層及びプーリング層などと、それに続く3層の全結合層から構成される
・畳み込み演算の部分から全結合層へのつなぎ
- Fratten : 13 x 13 x 256の画像を一列に並べる
- Global Max Pooling : 13 x 13 x 256の画像で各チャンネルの最大値を256個並べる
> 一気に情報量を減らして、効率的に特徴量を抽出できる
- Global Average Pooling : 13 x 13 x 256の画像を各チャンネルの平均値を256個並べる
> 一気に情報量を減らして、効率的に特徴量を抽出できる
・サイズ4096の全結合層の出力にドロップアウトを適用して、過学習を抑制
実装演習
【1_1_forward_propagation_after.ipynb】
・層数やノードの数を変えて、それぞれの入力と重みの内積にバイアスを加えた結果を計算
・平均二乗誤差や交差エントロピー誤差を計算しているが、学習せずに計算結果を出力するだけなので、層数やノード数を変えてもこれらの評価指標は改善しない。
【1_2_back_propagation.ipynb】
・入力(1.0, 5.0)に対して出力(0, 1)が得られるように、順伝播と逆伝播を実施
・初期値にて計算したところ、評価関数である交差エントロピー誤差の値は0.091

・更新された重みとバイアスの値に入れ替えて、再度、交差エントロピー誤差を計算したところ、0.087となり、改善された。


【1_3_stochastic_gradient_descent.ipynb】
・以下のコードの通り、更新するパラメータをランダムに選びながら、学習を実施(確率的勾配降下法)

・予測する関数が複雑ではないため、割と早い段階で学習が完了している。


【1_4_1_mnist_sample.ipynb】
・0~9の手書き文字の分類
・初期設定値にて、十分に学習が進んでいることを確認

・ミニバッチサイズを変えた場合、以下の結果となり、ミニバッチ降下法のメリットを実感
- 100の場合、計算完了まで9秒
- 10の場合、計算完了まで8秒
- 1000の場合、計算完了まで24秒
【2_1_network_modified.ipynb】
・1_4_1にて層を増やした場合にTestの正答率がわずかに向上した
(0.921 ⇒ 0.924)

【2_2_1_vanishing_gradient.ipynb】
・シグモイド関数では、勾配消失してしまい、学習が進んでいない

・勾配消失問題が発生しづらいReLU関数に変えてあげることで、学習が進むことを確認

・シグモイド関数でも初期値を適切に設定することで、勾配消失問題を回避することが可能(Xavier)

・ReLU関数でも初期値を適切に設定することで、さらなる精度向上を確認

【2_3_batch_normalization.ipynb】
・バッチ正規化を行うことで、学習が進むことを確認
- バッチ正規化無し

- バッチ正規化あり

【2_4_optimizer_after.ipynb】
・SGDを除いて、90%以上の正答率となった
・SGDでの正答率は11%だったが、バッチ正規化を行うことにより、71%まで向上させられることを確認した。

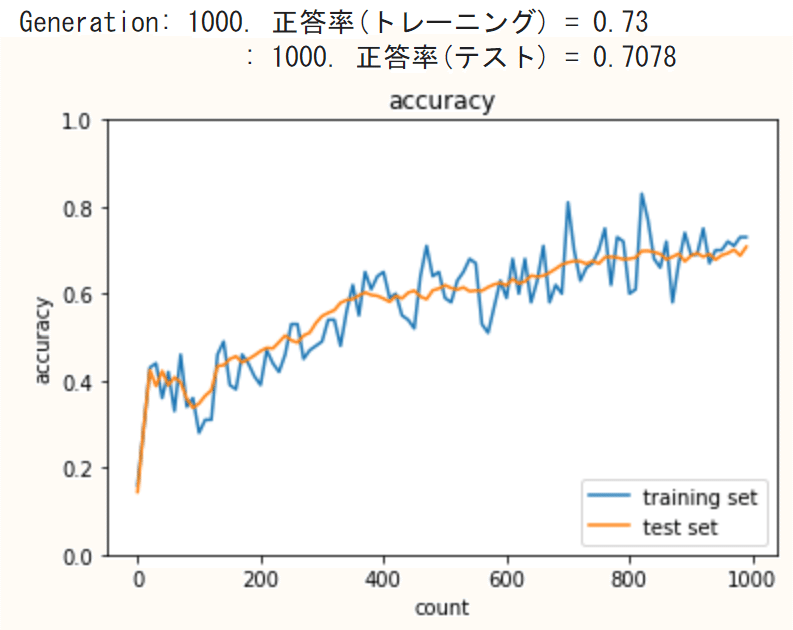
【2_5_overfitting.ipynb】
・初期状態ではtraining setとtest setの正答率の差が大きく、明らかに過学習が発生している
・L2正則化、L1正則化、Dropoutによって、training setとtest setの正答率の差を小さくしていくことが可能
・weight_decay_lambdaの値を変えたり、手法を組み合わせたりしながら、test setの正答率向上を目指すが、正則化が強くなりすぎて未学習になったり、なかなか最適解を目指すのは難しい。
- 初期状態

- L2正則化(weight_decay_lambda = 0.1)

- L2正則化(weight_decay_lambda = 0.2)

- L1正則化(weight_decay_lambda = 0.005)

- dropout

- dropout + L1正則化

【2_6_simple_convolution_network_after.ipynb】
・mnistの手書き文字のデータセットを題材に、シンプルなCNNを実装
・5000枚の訓練データと1000枚のテストデータに分割し、1000回のイタレーションで学習を実施
・95.5%の高い正答率が出た

【2_7_double_convolution_network_after.ipynb】
・2_6と同じデータセットを用いて、畳み込み層が2層となったネットワークにて学習を実施
・1層の畳み込みの場合と比較して、正答率は同程度だったが、層が増えてパラメータが増加したことにより、計算時間は約1.5倍となった。


【2_8_deep_convolution_net.ipynb】
・2_6、2_7と同じデータセットを用いて、ディープなネットワークで学習を実施
・認識率は1層、2層と比較して向上したが、その分、計算時間も長くなっている。
・1000回のIterationを実施したが、結果を見ると早い段階で正答率が高くなっているため、計算時間の短縮のためにも、半分の500回程度でも良かったと考えられる。

