機械学習(ラビットチャレンジ)
線形回帰モデル(単回帰、重回帰)
・線形とは比例(直線、平面、超平面)で予測可能
・バプニックの原理
- ランキング問題に回帰問題を用いるべきではない(密度比推定)
・教師あり学習
・パラメータwは最小二乗法で決定する
- 平均二乗誤差(残差平方和)Mean Squared Error
> データとモデル出力の二乗誤差の和
- 最小二乗法
> 学習データの平均二乗誤差を最小とするパラメータを選定
- 二乗損失は一般に外れ値に弱い(Huber損失、Tukey損失)
> 外れ値が無いことを確認した上で使用する
・誤差
- 偶発的な誤差だけでなく、考慮で来ていない説明変数がある可能性がある
・実装演習


非線形回帰モデル(線形モデルによる非線形回帰)
・線形回帰との違いは、xがφ(x)に変わったもの(一般化)
- φ(x)は基底関数と呼ぶ
・xは2乗になったり3乗になったりと非線形にはなるが、パラメータwについては線形(linear -in-parameter)
・過学習の対策
- 学習データの数を増やす
- 不要な基底関数(変数)を削除して、表現力を抑制
> 高次の無駄な変数を削除する
> どの変数を削除するかが難しいため、AICモデルを使う等
- 正則化法を利用して、表現力を抑制
> 変数ではなく、パラメータをゼロに近づける
・逆行列がない = 一次独立でない
・正則化法
> KKT条件
> パラメータwが大きくなると大きくなる罰則項を入れる
> Ridge推定(縮小推定) : パラメータをゼロに近づけるように
> Lasso推定(スパース推定) : いくつかのパラメータをゼロに
・ホールドアウト法
> 手元にデータが大量にある場合を除いて、良い性能評価を与えない
> 外れ値に対して弱い
・クロスバリデーション(交差検証)
- 外れ値の影響が小さくなる
・グリッドサーチ
- 全てのチューニングパラメータの組み合わせで評価値を算出
- 実装の練習はした方がよいが、実際はベイズ最適化(BO)がよく使われている
・実装演習(skl_nonlinear regression.ipynb)
- 非線形関数 + ノイズを与えたデータに対して、線形回帰、rbf_kernel(非線形)で予測
- スコアは0.275から0.809に改善


ロジスティック回帰モデル
・分類問題に適用
> 出力が0 or 1
・識別的アプローチ
> あるインプットxを入れた時に、確率を直接求めるように出力する
> ロジスティック回帰はこちら。
> Ckに属する確率が出せるところが嬉しい。
・生成的アプローチ
> ベイズの定理を経由して確率を求める
> 外れ値の検出ができる
> GANなどに使える(新たなデータを生成できる)
・識別関数
> f(x) > 0 ⇒ C =1, f(x) < 0 ⇒ C =0
> 例えばSVM
> 識別関数を作ってしまうと、Ckに割り当てられる確率が出せない(欠点)
・パラメータと変数をかけたものに、Sigmoid関数をかけて、0~1の範囲(確率)にする
・SIgmoid関数の微分はSigmoid関数で表現可能
・出力確率が0.5以上なら1、0.5未満なら0と分けられる
・尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という
・なぜ尤度関数でなく対数尤度関数を用いるか??
- 取りうる値が0~1のため、桁落ちしてしまうことを防ぐため。
・パラメータの更新には勾配降下法を用いる
・確率的勾配降下法
- ミニバッチ法の中でミニバッチ数が1の時のこと。


・実装演習(skl_logistic_regression.ipynb)
- タイタニックの生存者の分類をロジスティック回帰を用いて実装
- "Age"のカラムの欠損値は平均値で補完("AgeFIll")。
- ”Fare”のみ、また"AgeFill"、"Pclass_Gender"を説明変数として、"Survived"の予測を行ったが、以下の図の通り、2変数のケースの方が高い精度で分類できていることがわかる。

主成分分析
・少量変数を利用して、可視化や分析が可能
・分散が最大になるように次元削減を行う
> 分散が大きい = 情報・データがたくさん残っている
・実装演習(skl_pca.ipynb)
- ガンの良性、悪性の判断のため、ロジスティック回帰を用いて分類を実装
- 30個の説明変数を基に、test dataを97%の精度で分類することが可能との結果
- 特に寄与度の大きな2つの説明変数のみを抽出して、主成分分析を実施し、可視化

アルゴリズム
・k近傍法(kNN)
- kの値を変えると結果も変わる(教師無し学習のため)
- kを大きくすると決定境界は滑らかになる
・k-means
- 教師無し学習
- クラスタリング手法
- 初期値が近いとうまくクラスタリングできない
⇒ K-means++("機械学習アルゴリズム辞典"が参考資料)
・実装演習(skl_kmeans.ipynb)
- 3種類のwineのデータセットを用いて、k-meansによるクラスタリングを実施
- 正解である"species"と予測結果である"labels"をマトリックス表示してみると、両者が一致している数は少なく、うまくクラスタリングできていないことがわかる。

サポートベクターマシーン
・f(x) = 0が分類の境界
・分類境界を挟んで2つのクラスがどのくらい離れているかをマージンと呼び、このマージンが最大となるように分類境界を決める
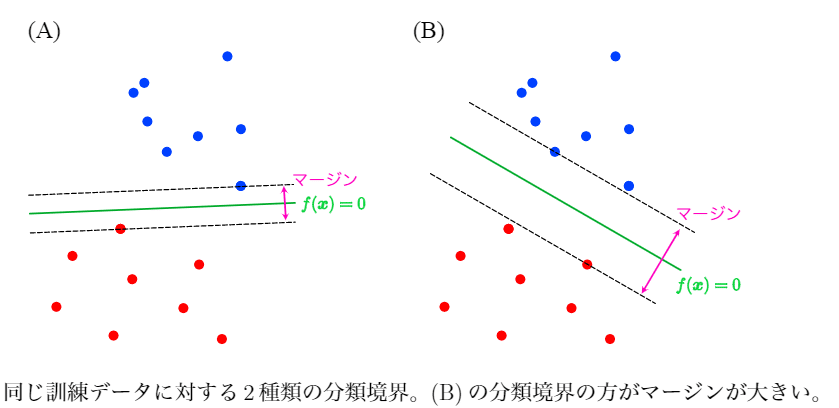
・すべてのデータを線形で分離可能と仮定したものをハードマージン、分離できないデータを許容したものをソフトマージンと呼ぶ
・線形分離できないケースに対しては、特徴ベクトルを非線形変換して、その空間で線形分類を行う「カーネルトリック」により、非線形分離も可能となる

・カーネル関数の代表的なものには以下の3つがある
- 多項式カーネル
- ガウスカーネル
- シグモイドカーネル
・実装演習(np_svm.ipynb)
- 線形分離可能なケース、線形分離不可能なケース、さらにデータに重なりがあるケースについて、SVMを用いて分類を実施
- 線形分離不可能な場合はRBFカーネルを用いて、データに重なりがある場合にはペナルティを加味した評価関数を導入して、以下の通り分類を実施。



