
Predictの自己組織化マップ機能で多次元データを俯瞰してみよう
1. ニューラルワークス Predictとは
ニューラルワークスPredictは、Microsoft Excel(以下、PredictおよびExcelと省略)上で、階層型ニューラルネットワークに基づく予測・分類モデルの構築、コホーネンの自己組織化マップ(Self-Organizing Map: SOM)[1]に基づくクラスタリング機能を持つツールです。前者は、予測および分類モデル構築用として、また後者は、多次元データの可視化・クラスタリング分析を行なうために用意されています。総じて、統計分析やニューラルネットワークの知識を前提とせず、初心者でも容易に操作可能なユーザー・インターフェイスを持っています。
本記事では、Predictの諸機能のうち、自己組織化マップ構築機能に焦点を絞って、その使用方法と簡単な事例紹介を行ないます。
2. SOM構築機能の基本操作
Predictのインストールが終了すると、Excelのアドインとして使用することができます。図1は、ベンチマークでよく使われる動物の特徴データセットをExcelで開いた例で、メニューにPredict(P)が追加されています。

Predictを使用する際には、分析用データはCSV形式あるいはExcelデータとして用意します。その際、列方向が各変数に対する値、行方向が各レコードとなるように並べます。
レコード数や変数の数がExcelの制限を越えてしまう場合は、コマンドラインインターフェイスにより、以下で説明するExcelでの操作に対応した処理を行うことができます(製品版のみ)。
3. SOMモデルの作成
図2: ExcelメニューのPredict(P)以下の機能リストを選択する画面(「新しいモデル」)が現れます。 SOMモデルの作成は、上画面上の4つのラジオボタンのうち、一番下の「データのクラスタ性の発見と解析」を選びます(図3)。

選択後、右下にある「次へ>」ボタンをクリックします。途中、2つの画面(「モデル構築ウィザード」および「自己組織化マップの構築(ステップ1の4)」)が現れますが、そのまま画面右下の「次へ>」ボタンをクリックしてスキップします。
「自己組織化マップの構築(ステップ2の4)」(図3.5)では、Excelワークシート上のデータ入力範囲を指定します。「最初の入力データ・レコード」テキストボックスには、1レコード目の範囲、「2番目の入力データ・レコード」には、2レコード目の範囲、「すべての入力データ」には、データセットの全範囲をマウスでドラックして指定します(図4, 図5)。


データ範囲の指定が終了したら、「次へ>」ボタンにより、次へ進みます(図6)。

図6では、2次元のコホーネン層の各次元のPE(プロセッシングエレメントの略。コホーネン層を構成するニューロン単位のこと。)数を入力します。ここで、3次元以上のマップを定義する場合には、次の画面(図3.7)の「詳細パラメータ・・・」で、追加入力します。入力が終了したら、「次へ>」ボタンにて最終画面(図7)に移動します。

最後に、「学習」ボタンのクリックによりネットワークの学習を開始します。学習が終了すると、学習終了画面が現れ、OKボタンにより終了します。
4. モデルからの出力
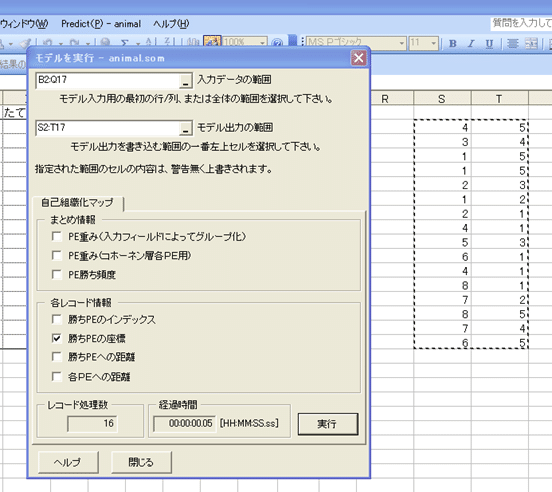
Excelメニューの「Predict(P)」à「実行」を選択する(図8)と「モデルを実行」ダイアログが現れます(図3.9)。

「各レコード情報」フレームの「勝ちPEの座標」のみにチェックを入れ、「モデル出力の範囲」で、出力先を指定後、右下の「実行」ボタンをクリックすると、各レコードに対する勝ちPE(ノード)の座標を出力することができます。
得られた出力結果に基づき、Excelが標準で装備している散布図機能を使ってマップを表示できますが、出力された座標と対応するレコードとの対応付けは、レコード数が多い場合には大変手間が掛かります。そこで、弊社では、ラベル付散布図を含む、Predict出力用の無償版Excelマクロをご提供しています。ご利用をご希望の方は、弊社製品担当 (ann@setsw.co.jp)までお問い合わせください。参考までに、図10は, 上記マクロによる散布図出力例です。

5. 株価時系列データへの適用例
最後に、SOMによる株価時系列データの可視化例について述べます。具体的には、ランダムに選ばれた株式上場企業393 社の2005 年1 月~2006 年9 月の週末および月末株価の終値の時系列変動に注目して、各銘柄間の相関関係を可視化することを試みました。
得られたマップは、着目していなかった相関性のある銘柄の発見や、リスク分散投資への活用等が考えられます。
SOM構築時の注意点としては、時間的変動に着目するため、入力データは株価の自身ではなく、以下で定義される変動値を利用したことです:
任意の週の変動値=週終値÷ (全92 週の週終値の平均)
任意の月の変動値=月終値÷ (全21月の月終値の平均)
。参考までに、株価自体を入力変数として使用した場合には、時間変動よりも株価の規模を反映したマップが構築されることが分かりました。
週変動値SOM(入力変数92 個)を図4.1に、月変動値SOM(入力変数21 個)を図4.2に示します。ただし、表示の都合上、393 社全てのデータではプロット数が多すぎて読み取り困難なため、各銘柄が属する業種の平均株価が上位の3 社のみを表示することとしました。
得られるマップからは、時間的に相関の高い銘柄同士は、それぞれ近傍の1 点として現れることになります。


いくつかの企業は、週および月でともに同一あるいは非常に近いものが存在します。例えば消費者金融系や異業種でも相関の高い銘柄が発見できます。
これらの企業は、短期および長期にわたり、株価変動が同期を取っており、リスク分散の観点でも注目に値するグループと考えられます。
ここでご紹介した例は、ある意味でエキスパートの投資家の大脳皮質にある株式市場像を可視化したと言え、初級から上級まで、さまざまなレベルの投資家にとっても、有益なマップとなるでしょう。
参考資料
[1] Teuvo Kohonen 著,徳高 平蔵,大薮 又茂,堀尾 恵一,藤村 喜久郎, 大北 正昭監修:'自己組織化マップ',シュプリンガー・ジャパン,2005年6月.
※弊社では、データ分析プロジェクトにまつわる様々なご相談に、過去20年以上に渡るプロジェクト経験に基づき、ご支援しています。社内セミナーの企画等、お気軽にご相談いただければ幸いです。
