データサイエンスを体感する - 02.STL分解を用いた時系列データの分析

ネットイヤーグループ公式note

2024年3月29日 17:54

今日も今日とてカフェでリモートワーク、データアナリスト/データサイエンティストMARU@ベローチェです。（ベローチェさん、いつもお世話になっております。先日、売り切れ必至の「黒ねこまみれグッズ」を無事ゲットしました）

さて前回の「01.クラスター分析」に続き、データ分析未経験/初心者の皆さま向けの体験企画の第2弾は「STL分解を用いた時系列データの分析」です。

例えば Google Analytics などで長期の時系列データを折れ線グラフで見たとき、グラフからどんな傾向があるのかをざっくり把握したいな・・なんてことはありませんか？・・時系列データとは、例えばこんなデータです。

これをサクッと把握したいときによく使う方法をご紹介しますね。

※事前に「00.Colaboratoryでのコード実行：初心者向けガイド」を目を通して準備してくださいね。

0. はじめに：STL分解とは？

STL分解（Seasonal and Trend decomposition using Loess）は、時系列データを季節成分（Seasonal）、トレンド成分（Trend）、そして残差成分（Residual）に分ける分析手法です。この分解を行うことで、データの挙動をより明確に理解し、予測や分析を行いやすくなります。季節成分は定期的なパターンを、トレンド成分はデータの長期的な傾向を、残差成分はこれらに含まれない不規則な変動をそれぞれ示します。

1. Pythonパッケージのインポートとその説明

分析を行う前に、必要なPythonパッケージをインポートします。

`pandas`: データの読み込み、加工、分析を行うためのライブラリです。
`numpy`: 数値計算を効率的に行うためのライブラリで、配列操作や数学関数などを提供します。
`matplotlib.pyplot`: データをグラフに可視化するためのライブラリです。
`statsmodels.tsa.seasonal`: 時系列データの季節性分析やSTL分解を行うための機能を持つライブラリです。

import pandas as pd # データ操作
import numpy as np # 数値計算
import matplotlib.pyplot as plt # 可視化
from statsmodels.tsa.seasonal import STL # STL分解

2. テストデータの作成

今回は、仮に「1年間の飲食店の売上データ」としてテストデータとして生成しましょうか。日別の売上金額のテストデータ（2023/1/1 - 2023/12/31 の1年間）を作成します。

np.random.seed(0) # 乱数シードの固定
date_range = pd.date_range(start="2023-01-01", end="2023-12-31", freq="D")
n = len(date_range)

data = {
    "date": date_range,
    "sales": np.round(
        np.random.normal(loc=200, scale=20, size=n) + # 基本の売上
        np.where(date_range.weekday < 5, 0, 50) + # 土日の売上増
        np.sin(np.linspace(0, 2 * np.pi, n)) * 30 + # 週単位の周期性
        np.where(date_range.month.isin([7, 8]), 100, 0) # 夏の売上増
    ).astype(int)
}

df_sales = pd.DataFrame(data)

次に、このデータの先頭15行を表示してみます。

print(df_sales.head(15))

日別の売上金額データができていると思います。（売上金額少ないですね・・すごくささやかなお店になっちゃう。単位（千円）だと思ってください）

元データの視覚化

作成した元の売上データを視覚化してみましょう。これにより、作成したテストデータの概観を把握できます。

plt.figure(figsize=(10, 6))
plt.plot(df_sales['date'], df_sales['sales'], label='Sales')
plt.title('Original Sales Data')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.legend()
plt.show()

（どうやら夏に売り上げが上がって秋冬に下がるお店みたいですね・・かき氷屋さん？）

もう少し短期で、4週間分のデータを視覚化して確認してみましょうか。

# 最初の4週間分のデータを選択
four_weeks_data = df_sales.loc[df_sales['date'] < "2023-01-29"]

plt.figure(figsize=(12, 6))
plt.plot(four_weeks_data['date'], four_weeks_data['sales'], marker='o', linestyle='-', label='Sales')
plt.title('Sales Data for the First Four Weeks')
plt.xlabel('Date')
plt.ylabel('Sales')
plt.xticks(four_weeks_data['date'], four_weeks_data['date'].dt.strftime('%m-%d (%a)'), rotation=90, fontsize=8)
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

この短期のグラフからは、どうやら週末（土曜、日曜）に売上が上昇する傾向があることが確認できます。これだけでもだいぶ傾向はつかめますが、STL分解して全体像を確認してみましょう。

3. STL分解の実行

今回のデータでは、先の確認から平日まずまず、土日に売り上げが上がる、というデータのようなので、週単位の周期（`period=7`）を考慮してSTL分解を行います。

# STL分解の実行
stl = STL(df_sales['sales'], period=7)
result = stl.fit()

# 各成分の抽出
df_sales['seasonal'] = result.seasonal
df_sales['trend'] = result.trend
df_sales['residual'] = result.resid

4. 結果の視覚化

最後に、STL分解の結果を可視化します。

plt.figure(figsize=(12, 9))

# 元のデータ
plt.subplot(411)
plt.plot(df_sales['date'], df_sales['sales'], label='Original')
plt.legend(loc='best')
plt.title('Original Data')

# 季節成分
plt.subplot(412)
plt.plot(df_sales['date'], df_sales['seasonal'], label='Seasonal')
plt.legend(loc='best')
plt.title('Seasonal Component')

# トレンド成分
plt.subplot(413)
plt.plot(df_sales['date'], df_sales['trend'], label='Trend')
plt.legend(loc='best')
plt.title('Trend Component')

# 残差成分
plt.subplot(414)
plt.plot(df_sales['date'], df_sales['residual'], label='Residual')
plt.legend(loc='best')
plt.title('Residual Component')

plt.tight_layout()
plt.show()

下記のような4つの時系列データに分かれて出力されると思います。

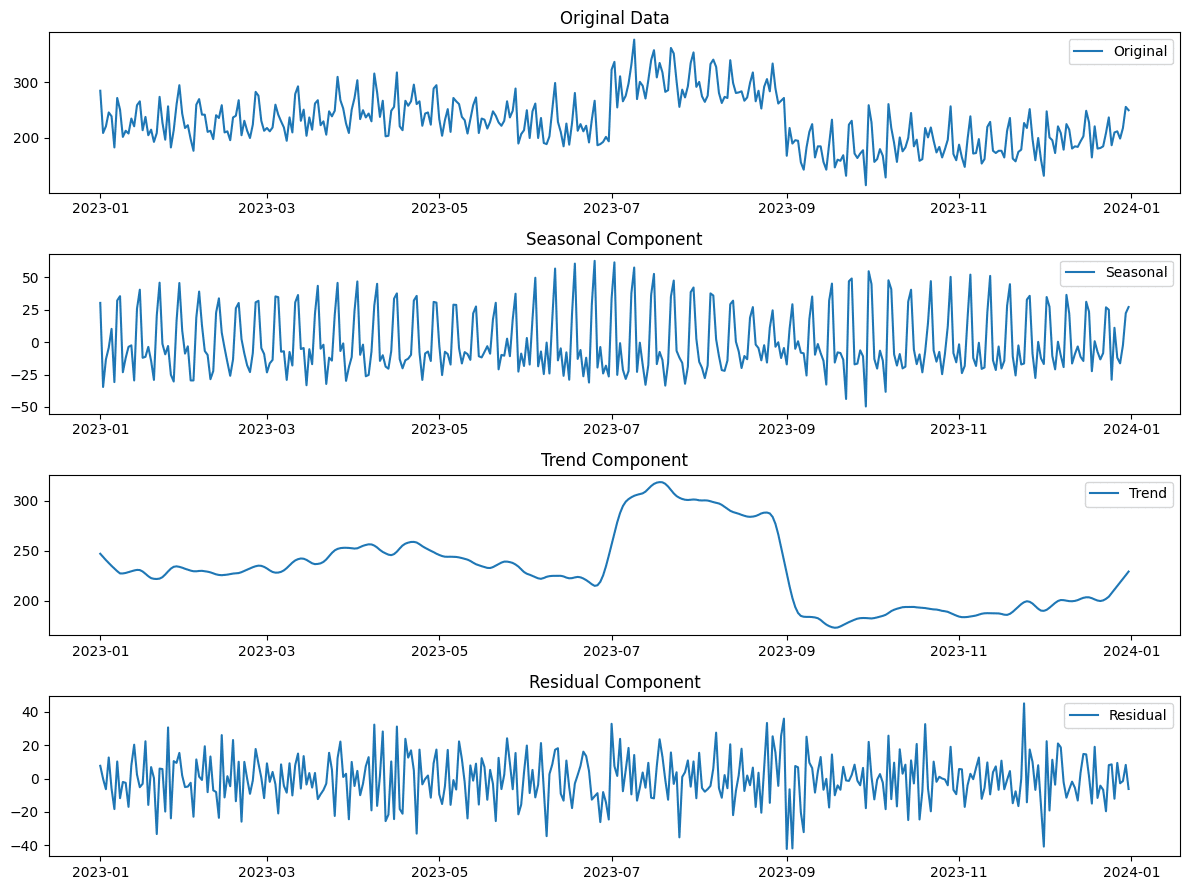
解説と解釈

原系列（Original）: これは元データそのものです。この例では、1年間の飲食店の売上データを示しています。原系列を分解することで、季節性、トレンド、その他の要因による変動を理解します。
季節成分（Seasonal）: データの短期的なパターンの把握です。データに含まれる周期的な変動を示しており、このケースでは週末に売上が上がるパターンの繰り返しを捉えていますね。これは、飲食店が週末に顧客が増えることを表しています。季節成分の抽出によって、データの周期的なパターンを明確に理解することができます。
トレンド成分（Trend）: データの長期的な変化を表しており、時間とともに売上がどのように変化しているかを示しています。週末の売上増加もこの中に反映されていますが、主に年間を通じた売上の上昇や下降の傾向を捉えています。トレンド成分によって、データの長期的な動向を理解することが可能になります。
残差成分（Residual）: 季節性やトレンドによって説明できないデータの変動、つまりモデルで捉えられない不規則な変動を示しています。これには、予期せぬイベントや外部からの影響などが含まれます。

ここではあまり気にしなくてよいですが、下記の式が成り立ちます。
　　元データ　＝　トレンド　＋　季節性　＋　残差

主に使うのは季節成分（Seasonal：短期のパターン）とトレンド成分（Trend：長期の傾向）です。元データの軽い確認とSTL分解で、今回の例では下記のことがざっくり把握でき説明しやすくなりますね。

土日に売り上げが上がる。
週単位で周期的なトレンドがあり、それを年間を通して繰り返している。
特に夏の時期（7月と8月）に売上が高くなる。

以上、STL分解を用いた時系列データの分析の基本的な流れとその視覚化、解釈についてご紹介しました。簡易な例ですが時系列分析の一端を体感いただければ幸いです。それではまた！