見出し画像

［√√2］A判の用紙サイズが思い出せないときの対処法

よねはらりゅうへい

文明崩壊後にA判の規格を復活させたいなら覚えておいてください

用紙サイズのA判の話です。日常に身近なA判と言えばおそらくA4でしょう。ですからA4が297×210ｍｍであることはなんとな〜く覚えているという人は多いと思います。

私もA4が297×210ｍｍであることは覚えているので、それを基にA3が420×297であることは暗算してわかるんですが、それ以外のA判のサイズはめんどくさくて覚えてないし暗算もしません。都度ググります。

数年前は任天堂の公式LINEに「A2」などと返信するとそのサイズを教えてくれたんですが、今はその機能は停止されています（案外便利だったのになぁ）。


とういうことで任天堂に頼ることもできなくなった令和の時代には(言い回しがおっさんのやつ)、紙のサイズは自分で調べなければなりません。とはいえ毎回ググるのめんどくさくて、スマホのメモにまとめたりしてみたものの、スマホが手元になく会話の中でサイズの話になったときには仕方なくスマホを取りに走ったりします。

職業上毎日紙のサイズに触れる方なら全部暗記していると思いますが、そこまでに至らないペーパー、じゃないペーペーの一般人はどうすれば良いのか？もし今、現代文明が崩壊して、もう一度A判の規格を復活させることになったらどうすればいいのか？

ということで、今回は手元にスマホがあるものの電波がなくてググれない時に、計算機だけを使って簡単にA判のサイズを確かめる方法を思いついたので書き残しておこうと思います。

A0のサイズを7タップで把握する

お手元にスマホがある方は、もしこのnoteをスマホで読んでいただいていたら恐縮ですが、計算機アプリを起動してください。

iPhoneの場合は画面を横向きにすると関数電卓になります。電卓をお使いの場合は√の計算ができるものをご準備ください。

iOS純正の計算機アプリ

まず数字の2を入れて、その平方根√2を求めます。一夜一夜に人見頃でお馴染みの数字が出てきたと思います。

2を入力し赤丸をつけたボタンで平方根を求めます

さらに、その1.41421356の平方根$${{\sqrt{1.41421356}}}$$を求めます。そうすると、1.189207114という数字が出てきます。

1.41421356の平方根を求めると
1.189207114という数字が出る

賢明なる読者はここで察しが着くと思う(一度言ってみたかった)。

この1.189207114という数字が、A0の長辺のサイズを教えてくれます。
すなわち1189ｍｍです。そして、この数字を√2で割ると、

0.84089641454という数字が出る

1.189207114÷√2＝0.84089641454…

ということで、A0の短辺が841ｍｍであることを教えてくれます。スマホを7タップすればA0の紙のサイズを把握できるのでA0導出タイムアタック大会があれば優勝ですし、消費カロリーもほぼ0です。ググらないので電子ゴミも増えません。

7タップでA0のサイズを確認できる

なぜこうなるのか

私はいま、√√2＝1.189207114という数字列からA0の長辺、√√2÷√2＝0.84089641454という数字列からA0の短辺が導けるから便利だぜ、という主張をしています。

もちろん、たまたまそうなる訳ではありません。そして、発見した私が偉い訳でもありません。この√√2や√√2÷√2という数字はA判の規格に備わっているものです。

つまり、

・A0は1㎡であること
・短辺と長辺の比は1：√2であること

というA判の規格の要件そのものを連立方程式にして式を変形すれば√√2や√√2÷√2という数字が出てきます。導出の数式そのものは打ち込むのがめんどくさいので、興味ある方は計算してください。

実際のA判のサイズに直すには1000倍してあげる必要があるので、そこだけは注意です。

あたらしいA判のサイズ一覧

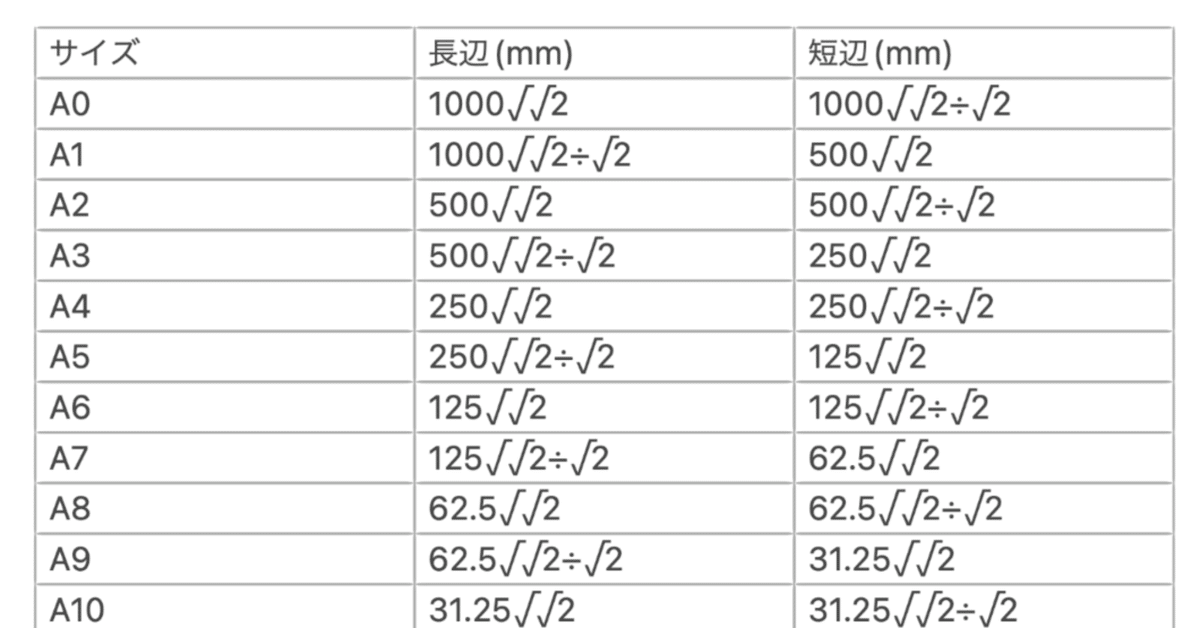
簡単にA0のサイズが求められることがわかったので、A1やA4のような他のサイズにも応用してみます。これがその一覧です。

A判のレシピ

…ということで、A判のサイズはこのような法則になっています(電卓で確かめてはいますが、計算ミスや検算ミスがあるかもです)。

個人的には、え〜とっ、長辺が半分、短辺がそのまま、端数が出て、四捨五入して…というこれまでの計算方法よりも規則性があって気に入ってます。

さらにこの計算方法が便利なのは、例えばA4を基準に297という数字を2倍したり、2で割ったりした場合は四捨五入の過程で誤差が生まれてしまいますが、今回の計算方法はA判規格の定義そのものなので、誤差が出ません。

√√2

297×210というような無機質で無個性に見える数字の裏側、規則がわかることで、なんとなく愛着が湧いた感じがします。理屈がわかれば暗記もできそうです。

最終的には白銀比ってすごい！という結論になってしまうのですが、√√2という確認方法は面白いと思うので、よければ覚えておいてください。飲み会での話のネタくらいにはなるかと思います。

このnoteが何かの参考になれば幸いです。最後まで読んでいただきありがとうございました！

書いている人：＠YoneharaRyuhei


いいなと思ったら応援しよう！

よねはらりゅうへい
ぼくのnoteを読んでいただきありがとうございます！写真、カメラ、美術などいろんな記事を書いていきますので、すこしでも面白いと思っていただけたならサポートをお願いします‼