
【プリコネR】割り振りを解く
クラバトお疲れ様でした.ぺたふぁん(存在しないクラン)のねりうめです.
本記事では,現代クラバトの一要素である「割り振り」を機械にお願いする手法について解説/考察します.以下で取り上げる手法は,実際にぺたふぁんで行われていないものを含みます.
誰かAI進行クラン作ってください.
「組む」と「解く」
初日パズルは「組む」ものとされていますが,一般的なパズルは「解く」ものですよね.この違いは何でしょうか?

ぺたふぁん鯖で相談した結果,「メインの動作が『問題を解く』かどうか」で区別されているのではないかということになりました.


個人的にもう少し考えてみたのですが,「それを行う人間が主として使うものが頭なのかどうか」がしっくりきています.
例えば,我々からしたら1桁同士の足し算は「解く」というよりも「書く」ですが,足し算を習いたての人からしたら「解く」になるでしょう.
また,プログラマの界隈では「あとは書くだけ」というフレーズが存在します.これは,「ある問題を解決するための手法は思いついたので,それを実装するフェイズに入った」という意味です.
他クラン様の事情をあまり把握していないのですが,おそらく
「30人分の凸ルートを決める」→「ルートをに対し編成を当てはめる(進行側がやるかはクランによりけり)」といった手順で進めていると思います.
2023/08以前は「ルートに対し編成を当てはめる」ことが容易であったためS帯であれば貫通180凸余裕な環境でしたが,2023/09のN消滅アプデにより一気に難度が上昇しました.いわゆる「組み立てる」アプローチでは,割り振り作成にかなりの時間を要しているのではないでしょうか?
そこで,割り振りを「組む」のではなく「解く」手法について紹介します.
この手法では,「仮割り振り表に対応する編成情報を探す」ことで割り振りを作成します.完成状態のジグソーパズルからピースの組み合わせを逆算するようなものです.

割り振りを「解く」手法は以下のような特長があります.
誰でも作れる
複雑な操作やプログラムの知識を(利用する際には)必要としない
スプシとGASで完結
簡単に作れる
仮割り振り作成,編成登録,解くボタンの3ステップ
不成立時の追加対応は必要
すぐ作れる
編成登録済の状態であれば数秒
編成登録もそんなにかからない
実装例は以下のスプレッドシートを参照ください.
この先で紹介する内容も全てこのスプレッドシートに格納してあります.
凸ルートの成立条件
準備として,どのような凸ルートであれば成立するかをおさらいします.
また,編成情報を入力したとき,凸ルートとして成立しているか調べるものを作ります.
持ち越しを考えない場合(スプレッドシート)
以下の画像のルートが成立しているか考えてみてください

2023/09クラバトで見たことあります.1物-3物-5物です.
成立していますね.

では,手始めに「編成情報を入力したとき,その編成が成立しているかどうか判定するスプシ」を作ってみましょう.入力側がサポ借りキャラを指定できれば簡単なのですが,どのキャラを借りればよいか,という情報まで出力してもらうにはどうすればよいでしょうか?


これも成立しますね

これは成立しません 一瞬でわかりますか?
直感的なものとしては,「それぞれの凸から1キャラをいい感じに選んで消したとき,残った4キャラ×3編成が全て別々のものとなる」わけですが,じゃあそのキャラをどうやって選ぶんだという問題があります.人間はこの辺よしなにやってくれるのですがね.
では,2段階に分けて考えてみましょう.
1段階目は「ルートとして成立しているかどうか」
2段階目は「どのキャラを借りるか」
です.
1段階目: ルートとして成立しているかどうか
ルートとして成立しているかどうかは,キャラの重複状況から求められます.(借りなければいけないキャラ数が3キャラ以下) かつ (2編成を選んだとき,重複キャラが2キャラ以下)です.
借りなければいけないキャラは,出現するキャラのリストから求められます.5*3の15キャラにおいて,(出現回数-1)回をサポ借りする必要があります.
もちろん,3凸では3回までしかサポ借りできないため,この値が4以上になればルートとして不成立です.
また,借りなければいけないキャラが3キャラであっても,2つの編成において3キャラが被っていれば成立しませんね.3キャラ被りでも成立するのは,
1凸目: キャラA, キャラB
2凸目: キャラB, キャラC
3凸目: キャラA, キャラC
という重複状況の場合です.
では,まずこれらを判定するものを作ります.
「キャラ名を一意にしたもの」と「それが何凸目で出てきたもの」を取得し,そこからルートの成立を確認します.

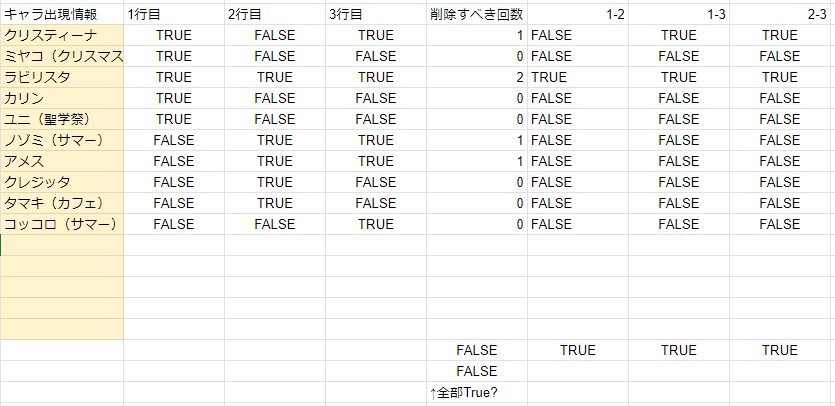
借りなきゃいけないキャラが4回分
2段階目: どのキャラを借りるか
借りるべきキャラの種類数によって場合分けしましょう.
借りるべきキャラが0種類の場合
おめでとうございます.
借りるべきキャラが1種類の場合
そのキャラを借りれば終わりです.
借りるべきキャラが2種類の場合
2種のキャラA,Bを使用しているかを,それぞれの凸ごとに調べます.
ここで,
AとBの両方を使用している場合
両方使用が1回目であればAを借りる
両方使用が2回目であればBを借りる
(3回目はルートが存在しない)
AとBの片方のみ使用している場合
そのキャラを借りる
ことで,どのキャラを借りればよいかわかります.
借りるべきキャラが3種類の場合
キャラA,B,Cの3種を3凸で借りることになるため,それぞれの凸において別々のキャラを1回ずつ借りることになります.つまり,サポ借りパターンは6通りです.1,2,3凸目において,
A, B, C の順で借りる
A, C, B …
B, A, C
B, C, A
C, A, B
C, B, A
この6通りにおいて,「そのキャラが編成に存在しているかどうか」と「そのキャラを借りたとき,他12キャラがユニークになるか」を判定します.
ルートとして成立しているため,必ず1つは成立する組み合わせがあります.
ここまでで,すべての場合で判定できるようになったので,対応するキャラの種類の部分の値を持ってくればよいです.
というわけで,持ち越しを考慮しない3凸編成については,機械にお願いできるようになりました.
スプレッドシートの関数のみで実装できましたね!
持ち越しを考える場合(GAS)
先程は3凸でしたが,今回は6凸分考慮する必要があります.
また,条件として,持ち越しであればキャラの重複が許容されますね.
借りるキャラの変更もできます

スプシの関数のみで実装するのは大変そう……
総当りのアプローチ
先程の議論より,「借りるキャラ」というのは「複数回登場するキャラ」ですね.そこで,「複数回登場するキャラを片っ端から借りてみる」というアプローチを考えることができます.これは現実的でしょうか?
最悪の場合を想定するため,「複数回登場するキャラ」という条件を省き1凸目から3凸持ち越しまですべてのパターンのサポ借りを試してみましょう.1編成につき5キャラ,6編成あるためサポートの選び方は5^6=15625通りあります.実は,このくらいの場合の数ではコンピュータはびくともしません.余裕です.
実際には,「複数回登場するキャラ」に対してのみ試せばよいため,多く見積もっても5000通り程度でしょう.余裕です.
では,この方針をもとに実装してみましょう.できたものがスプシにあります.以下のような手順で動いています.
キャラのリストをセルから読み込む
重複しているキャラを取り出す
重複しているキャラを各編成から1キャラ外したときの組み合わせを全パターン作る
その編成が成立しているかどうか確認する
ここまでの準備により,編成の組に対して凸ルートが成立するかを判定できるようになりました.
では,ここから,「初日割り振りを解く」ものを作っていきましょう.
初日割り振りを解く
繰り返しになりますが,ここで言う「初日割り振りを解く」は,「予め作った凸ルート一覧に対応する編成を求める」ことです.
そのために,まずは編成の置き場を作りましょう.
編成データベースをつくる
GASで読み込めるような形式で編成情報を置ければなんでも構いません.
凸先,ダメージ,討伐時間,キャラ名さえあればよいと思います.

探索システムをつくる
いよいよ本体です.希望凸ルートを入力したとき,対応する編成を出力します.
できたものがスプシにあります.
以下のような手順で動いています.
各行に入力された6つの凸先の編成のリストを作る
編成のリストから,各凸先につき1つの編成を選ぶ
2をすべてのパターン分作る
「持ち越しを考える場合」で作ったスクリプトへ編成情報を渡し,ルートの成立を確認する
成立してたら次の行へ してなければ総当りを続ける
不成立の場合
対応するパズルのピースがないので,探すなり作るなりしましょう.
存在するピースを自動で組み合わせてもらうことはできますが,
ピース本体を作ってもらうことはできません.
課題
VHの秒数欠損問題について放置しています.
運用で解決的な方法であれば,DBに「その他」で登録すればよいです.ダメージスイング解析ツールと組み合わせれば解決しそう
各自のキャラ持ちや活動時間の情報を紐付ければ
もっと適切な割り振りを作成できそう.
おわりに
誰かAI進行クラン作ってください.
おまけ: 2日目のルートごとの人数算出
明日は,1魔15凸 2魔20凸 3物20凸 4物20凸 5魔15凸 の割り振りにしたい.
各ルートごとの人数はどうなる?
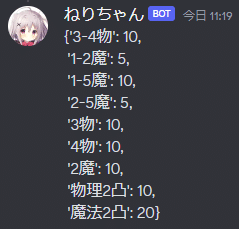
人力で解く
こういう形式のスプレッドシートを使って解くことができます.

上に凸先を記入し,下に凸先に対応する部分の凸数を入力します.
すべてを足した値が右に表示されるので,これが一致すればOKです.
機械で解く: 連立方程式
1物から5魔までの必要凸数を入力すると,それぞれの凸ルートごとの人数を出力するものを考えます.
1物から5魔までそれぞれ最大1凸ずつであれば,凸ルートは10C3=120通りあります.
ここで,1物-2物-3物を通る凸ルートの人数を1b2b3b, 4物-5物-1魔を通る凸ルートの人数を4b5b1mのように置きます.
このとき,
(入力された1物の必要凸数)=(1bが含まれる人数の総数)
(入力された1物の必要凸数)=(2bが含まれる人数の総数)
…
になればよいです.
つまり,以下のような問題を解ければよいわけです.
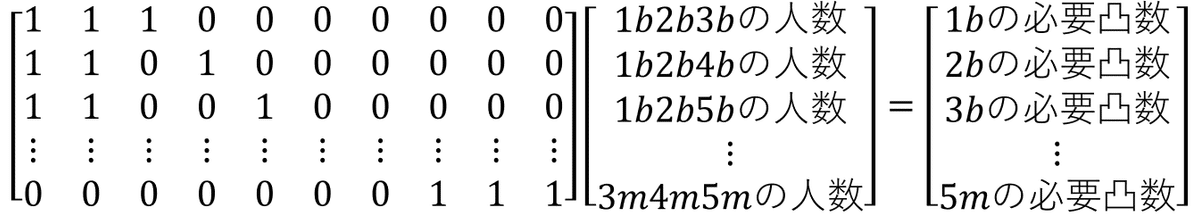
ただの連立一次方程式になりました.嬉しいですね.
しかし,この問題の解を直接求めるのは困難です.悲しいです.
解が不定になるためです.
自分が知る限りでは「不定解のとき,その解のうち1つを出力する」アルゴリズムは探索的もしくは反復的なものになります.


これを書いてて気が付きましたが,不定解に対していい感じの追加条件を付与すればそのまま解ける気がしています.後は頼みました.
スプシのGASで解ければ嬉しいのですが,このアプローチは一旦諦めます.
Python(Discordのbot)では各種ライブラリを使用可能ですので別のアプローチを取ることができます
機械で解く: SATソルバ
SATソルバとは,充足可能性問題(SAT; Satisfiability problem)を解くことができる(可能性がある)ツールです.
充足可能性問題とは,与えられた論理式を真にする変数割当てを求める問題です.
身の回りにある問題としては,パズル(数独,8クイーン)やスケジューリング問題が充足可能性問題に置き換えられます.
http://www.swlab.cs.okayama-u.ac.jp/lab/nom/articles/matsuda-ri-20221013-162413
与えられた論理式を真にする変数割当て,なんだかこの問題にぴったりですね.
ねりちゃんの機能もz3-solverというSATソルバを用いて実装しています.以下に実装例を示します,汚いコードなので恥ずかしいですが.
z3に関する詳細は以下サイトが詳しいです.
async def solve_route(self, ctx, p1, p2, p3, p4, p5, m1, m2, m3, m4, m5, ban_route=""):
r12p, r13p, r14p, r15p, r23p, r24p, r25p, r34p, r35p, r45p = Ints(
"r12p r13p r14p r15p r23p r24p r25p r34p r35p r45p")
r12m, r13m, r14m, r15m, r23m, r24m, r25m, r34m, r35m, r45m = Ints(
"r12m r13m r14m r15m r23m r24m r25m r34m r35m r45m")
r1p, r2p, r3p, r4p, r5p = Ints("r1p r2p r3p r4p r5p")
r1m, r2m, r3m, r4m, r5m = Ints("r1m r2m r3m r4m r5m")
ban_list = ban_route.split(" ")
r12pb, r13pb, r14pb, r15pb, r23pb, r24pb, r25pb, r34pb, r35pb, r45pb = Bools(
"r12pb r13pb r14pb r15pb r23pb r24pb r25pb r34pb r35pb r45pb")
r12mb, r13mb, r14mb, r15mb, r23mb, r24mb, r25mb, r34mb, r35mb, r45mb = Bools(
"r12mb r13mb r14mb r15mb r23mb r24mb r25mb r34mb r35mb r45mb")
r12pb = True if "r12p" in ban_list else False
r13pb = True if "r13p" in ban_list else False
r14pb = True if "r14p" in ban_list else False
r15pb = True if "r15p" in ban_list else False
r23pb = True if "r23p" in ban_list else False
r24pb = True if "r24p" in ban_list else False
r25pb = True if "r25p" in ban_list else False
r34pb = True if "r34p" in ban_list else False
r35pb = True if "r35p" in ban_list else False
r45pb = True if "r45p" in ban_list else False
r12mb = True if "r12m" in ban_list else False
r13mb = True if "r13m" in ban_list else False
r14mb = True if "r14m" in ban_list else False
r15mb = True if "r15m" in ban_list else False
r23mb = True if "r23m" in ban_list else False
r24mb = True if "r24m" in ban_list else False
r25mb = True if "r25m" in ban_list else False
r34mb = True if "r34m" in ban_list else False
r35mb = True if "r35m" in ban_list else False
r45mb = True if "r45m" in ban_list else False
solver = Solver()
solver.add(
r12p + r13p + r14p + r15p + r1p == p1,
r12p + r23p + r24p + r25p + r2p == p2,
r13p + r23p + r34p + r35p + r3p == p3,
r14p + r24p + r34p + r45p + r4p == p4,
r15p + r25p + r35p + r45p + r5p == p5,
r12m + r13m + r14m + r15m + r1m == m1,
r12m + r23m + r24m + r25m + r2m == m2,
r13m + r23m + r34m + r35m + r3m == m3,
r14m + r24m + r34m + r45m + r4m == m4,
r15m + r25m + r35m + r45m + r5m == m5,
r12p + r13p + r14p + r15p + r23p + r24p + r25p + r34p + r35p + r45p +
r12m + r13m + r14m + r15m + r23m + r24m + r25m + r34m + r35m + r45m <= 30,
r12p + r13p + r14p + r15p + r23p + r24p + r25p + r34p + r35p + r45p +
r12m + r13m + r14m + r15m + r23m + r24m + r25m + r34m + r35m + r45m <= 30,
r1p + r2p + r3p + r4p + r5p + r1m + r2m + r3m + r4m + r5m <= 30,
r12p + r13p + r14p + r15p + r23p + r24p + r25p +
r34p + r35p + r45p == r1m + r2m + r3m + r4m + r5m,
r12m + r13m + r14m + r15m + r23m + r24m + r25m +
r34m + r35m + r45m == r1p + r2p + r3p + r4p + r5p,
If(r12pb, r12p == 0, r12p >= 0),
If(r13pb, r13p == 0, r13p >= 0),
If(r14pb, r14p == 0, r14p >= 0),
If(r15pb, r15p == 0, r15p >= 0),
If(r23pb, r23p == 0, r23p >= 0),
If(r24pb, r24p == 0, r24p >= 0),
If(r25pb, r25p == 0, r25p >= 0),
If(r34pb, r34p == 0, r34p >= 0),
If(r35pb, r35p == 0, r35p >= 0),
If(r45pb, r45p == 0, r45p >= 0),
If(r12mb, r12m == 0, r12m >= 0),
If(r13mb, r13m == 0, r13m >= 0),
If(r14mb, r14m == 0, r14m >= 0),
If(r15mb, r15m == 0, r15m >= 0),
If(r23mb, r23m == 0, r23m >= 0),
If(r24mb, r24m == 0, r24m >= 0),
If(r25mb, r25m == 0, r25m >= 0),
If(r34mb, r34m == 0, r34m >= 0),
If(r35mb, r35m == 0, r35m >= 0),
If(r45mb, r45m == 0, r45m >= 0),
r1p >= 0,
r2p >= 0,
r3p >= 0,
r4p >= 0,
r5p >= 0,
r1m >= 0,
r2m >= 0,
r3m >= 0,
r4m >= 0,
r5m >= 0,
)
if solver.check() == sat:
m = solver.model()
ans = [
m[r12p].as_long(),
m[r13p].as_long(),
m[r14p].as_long(),
m[r15p].as_long(),
m[r23p].as_long(),
m[r24p].as_long(),
m[r25p].as_long(),
m[r34p].as_long(),
m[r35p].as_long(),
m[r45p].as_long(),
m[r12m].as_long(),
m[r13m].as_long(),
m[r14m].as_long(),
m[r15m].as_long(),
m[r23m].as_long(),
m[r24m].as_long(),
m[r25m].as_long(),
m[r34m].as_long(),
m[r35m].as_long(),
m[r45m].as_long(),
m[r1p].as_long(),
m[r2p].as_long(),
m[r3p].as_long(),
m[r4p].as_long(),
m[r5p].as_long(),
m[r1m].as_long(),
m[r2m].as_long(),
m[r3m].as_long(),
m[r4m].as_long(),
m[r5m].as_long(),
]
# 出力を整形
ansdic = {}
if (ans[0] != 0):
ansdic["1-2物"] = ans[0]
if (ans[1] != 0):
ansdic["1-3物"] = ans[1]
if (ans[2] != 0):
ansdic["1-4物"] = ans[2]
if (ans[3] != 0):
ansdic["1-5物"] = ans[3]
if (ans[4] != 0):
ansdic["2-3物"] = ans[4]
if (ans[5] != 0):
ansdic["2-4物"] = ans[5]
if (ans[6] != 0):
ansdic["2-5物"] = ans[6]
if (ans[7] != 0):
ansdic["3-4物"] = ans[7]
if (ans[8] != 0):
ansdic["3-5物"] = ans[8]
if (ans[9] != 0):
ansdic["4-5物"] = ans[9]
if (ans[10] != 0):
ansdic["1-2魔"] = ans[10]
if (ans[11] != 0):
ansdic["1-3魔"] = ans[11]
if (ans[12] != 0):
ansdic["1-4魔"] = ans[12]
if (ans[13] != 0):
ansdic["1-5魔"] = ans[13]
if (ans[14] != 0):
ansdic["2-3魔"] = ans[14]
if (ans[15] != 0):
ansdic["2-4魔"] = ans[15]
if (ans[16] != 0):
ansdic["2-5魔"] = ans[16]
if (ans[17] != 0):
ansdic["3-4魔"] = ans[17]
if (ans[18] != 0):
ansdic["3-5魔"] = ans[18]
if (ans[19] != 0):
ansdic["4-5魔"] = ans[19]
if (ans[20] != 0):
ansdic["1物"] = ans[20]
if (ans[21] != 0):
ansdic["2物"] = ans[21]
if (ans[22] != 0):
ansdic["3物"] = ans[22]
if (ans[23] != 0):
ansdic["4物"] = ans[23]
if (ans[24] != 0):
ansdic["5物"] = ans[24]
if (ans[25] != 0):
ansdic["1魔"] = ans[25]
if (ans[26] != 0):
ansdic["2魔"] = ans[26]
if (ans[27] != 0):
ansdic["3魔"] = ans[27]
if (ans[28] != 0):
ansdic["4魔"] = ans[28]
if (ans[29] != 0):
ansdic["5魔"] = ans[29]
ansdic["物理2凸"] = ans[0] + ans[1] + ans[2] + ans[3] + \
ans[4] + ans[5] + ans[6] + ans[7] + ans[8] + ans[9]
ansdic["魔法2凸"] = ans[10] + ans[11] + ans[12] + ans[13] + \
ans[14] + ans[15] + ans[16] + ans[17] + ans[18] + ans[19]
ansstr = ""
for i in ans:
ansstr += f"{i},"
await ctx.send(ansstr)
await ctx.send(pprint.pformat(ansdic, sort_dicts=False))
# 出力をフォーマット
else:
await ctx.send(f"ルートが存在しないよ~~~")探索的な実装よりもこっちのほうが早いと思います.
注意点として,z3はそこそこ重いので動作環境に気をつけたほうが良いです.ラズパイ3では`pip install z3-solver`を実行したら発熱なのか何なのかわからないですがとりあえずラズパイ本体が落ちていました.4なら耐えた.
