
ゲーム理論で考える人間関係
経済学部経済学科卒iOSエンジニアの田畑浩平です。
先日書いた👇こちらの記事は6,000回ほど読まれ、「現実世界での事象を経済学で説明する」記事に需要がありそうだったので、今回も経済学の記事を書いていきたいと思います。
今回は、けんすうさんを始めとする多くの経営者の方が説いている
・多くを得るためにはまずはギブする/信頼すること
・多くを得るためにはしっぺ返し戦略使うといいよ
あたりの話をゲーム理論の枠組みで解説しようと思います。
囚人のジレンマでは一番多くを得るには、基本的にギブしつつ、相手になにかされたらしっぺ返し戦略をとり、たまに許す、というのが一番いいらしいので、その通りにやってますhttps://t.co/nwcN4TZFJ5 #MySarahah @sarahah_com pic.twitter.com/WbYCL4Ghhi
— けんすう@マンガサービスのアル (@kensuu) December 12, 2017
うまくいく人は、まず「ギブ」から始めている。たとえば、ツイッターやnoteでノウハウを無料公開、それが編集者の目に止まり出版、ブランドができ、仕事もやって来る。うまくいかない人は「テイク」ばかり。お金やノウハウを手に入れても、がっちり抱え込んでシェアしない。それでは次につながらない。
— 竹村俊助/編集者 (@tshun423) December 15, 2019
よく「リモートだとどう信頼関係築くのか?」と質問されるのですが、そういう人が間違ってるのは「相手が何かを与えてくれたら信頼できる」という考え方。無条件にまず相手を信頼する!というか自分がまず信頼するところから始まる、という姿勢がない人はすごく損してる気がする
— 石倉秀明@かんたん募集サービスbosyu (@kohide_I) June 26, 2018
そもそもゲーム理論って?
そもそも、ゲーム理論とはどういったものなのでしょうか。
ゲーム理論は経済学の一分野で、以下の本👇などでは「複数の意思決定をする主体が、その意思決定に関して相互作用する状況を研究する理論」と説明されています。
これを噛み砕いて説明すると、
・ある一方の意思決定が、もう一方の意思決定に影響を与えるような問題
(例:二国間の軍拡競争など。こちらの出方(軍拡する or しない)が相手の出方に影響を与えるタイプの問題)を研究する学問ということになります。
「一方の意思決定が他方の意思決定に影響を与える状況」というのは人間関係から政治、経済・経営、ボードゲームにいたるまで、社会の中でどこにでもあるものなので、割と広範に使える理論になっています。
「囚人のジレンマ」って?
では、けんすうさんもツイートの中で言及している「囚人のジレンマ」とはどういったものなのでしょうか。
「囚人のジレンマ」では、ある事件の犯人と思われる容疑者1、容疑者2に自白させるような状況を考えます。

この2人の容疑者は、お互いに意思疎通ができない状態で、別々に取り調べを受けています。

それぞれの部屋で容疑者は以下のような司法取引を持ちかけられます。
・お前達は本来なら懲役5年
・2人とも黙秘した場合は、証拠不十分で2人とも懲役2年
・1人が自白、1人が黙秘した場合、自白した方は懲役なし、黙秘した方は懲役10年
・2人とも自白した場合は、本来の求刑通り2人とも懲役5年
これを利得表と呼ばれる表にまとめると以下のようになります。
(※ちなみに、カッコ内は(容疑者1の懲役、容疑者2の懲役)です)
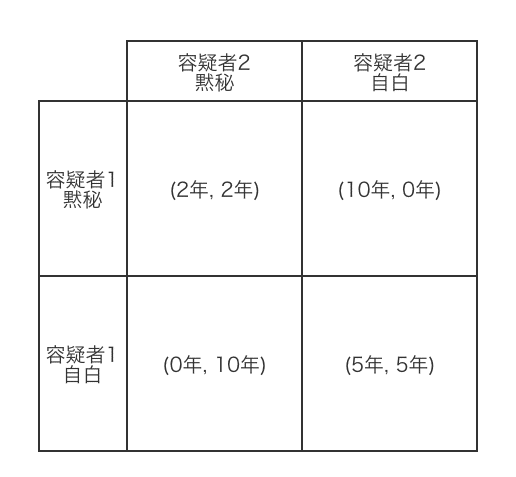
この表からわかるように、最も得なのはお互いに黙秘し、懲役を2年で済ませることです。しかし、容疑者1、2が自分の利益を追求すると自白が最適な行動(相手の行動が黙秘・自白のいずれであっても、自白するほうが懲役が短い)となり、お互いに自白してしまいます。
これが「囚人のジレンマ」と呼ばれる所以です。
有限/無期限繰り返しゲームについて
黙秘を「協調」、自白を「裏切り」と言い換えると、1回限りの取引の場合、裏切りが最適な戦略であることを見てきました。
これを複数回繰り返す場合や、無限回繰り返す場合はどのような戦略が最適なのでしょうか。
取引が有限回でかつプレイヤーが取引の回数を知っているケースは「有限繰り返しゲーム」と呼ばれ、プレイヤーは全ての取引において裏切りを選択することが知られています(ゲームの最終回では裏切りが最適→その1回前の選択は最終回での選択に影響を与えない、従って裏切りが最適→...これを1回目までさかのぼって考える後退機能法で示すことができる)。
プレイヤーが取引の回数を知らない「無期限繰り返しゲーム」と呼ばれる状況ではどうなるでしょうか。いつがゲームの最終回かわからないため、最終回からさかのぼって戦略を考えることができません。
このようなケースにおいて、プレイヤーがゲーム全体から得られる利益を最大化しようとすると、裏切りはそれほどお得な選択肢ではないことは明らかです(1回は自分:裏切り/相手:協調で得できるかもしれないが、その後は自分:裏切り/相手:裏切りのジレンマ状態に落ち着くため)。
しっぺ返し戦略の登場
1980年、アメリカの政治学者ロバート・アクセルロッドは、このような無期限繰り返しゲームの最適な戦略について考えてみようと思い、様々な分野の研究者から戦略を募集し、各戦略を実装したコンピュータプログラムを総当り対戦させる、という実験を行いました。
第1回の実験では、「1回目は協調する。2回目以降は直前の相手の行動を選択する(相手が協調を選択していた場合、こちらも協調を、相手が裏切りを選択していた場合、こちらも裏切りを選択)」というしっぺ返し戦略が優勝し、打倒「しっぺ返し戦略」を期して行われた第2回の実験でもしっぺ返し戦略が優勝するという結果に終わりました。
人間関係としっぺ返し戦略
これを日常生活における人間関係、取引に置き換えてみましょう。
日常生活における人間関係や取引は
・終わりが事前に決められていることは滅多にない
・互いに裏切るより協調を選択したほうが多くを得やすい
という特徴を持っており、無期限繰り返しゲームの一種と考えることができるのではないでしょうか。
そして、無期限繰り返しゲームの一種と考えることができるのなら、無期限繰り返しゲームにおける最適な戦略であるしっぺ返し戦略を選択することでより多くのものを得られるのではないでしょうか。
まとめ
今回は、
・現実の人間関係を抽象化すると無期限繰り返しゲームと見なせる
・無期限繰り返しゲームとすると、しっぺ返し戦略は割と有効な戦略
ということを解説してみました。
ゲーム理論は、大学で学んだ内容のうち、実生活でも使えるシーンが多いと感じる理論ですので、これを機に興味を持っていただけると幸いです。
文章的な説明だけでなく、実際の計算なども見てみたいと思われた方には以下の本もオススメです。
いいなと思ったら応援しよう!

