見出し画像

定量分析のはじめかた４

nekoyoshiko

今回は「資本資産価格モデル」、CAPMについて解説をいたします。理論的な背景は大事にしつつ、Pythonによるコード事例を紹介した解説を行っています。

資本資産価格モデル（CAPM）とは？

資産の期待リターンと市場のシステマティックリスクの関係を説明するものです。この式から、資産が市場全体に対してどれだけリスクを持つのか、そしてそのリスクに対してどれだけのリターンが期待できるのかを計算することができますね。

システマティックリスク（Systematic Risk）とは、分散投資を行っても消去しきれないリスクのことである。例えば、景気の悪化のようなマーケット全体に影響をもたらすような変動があげられる。CAPMでは、システマティックリスクのみが期待リターンに影響を与える。

https://glossary.mizuho-sc.com/faq/show/162?site_domain=default（ファイナンス用語集）

CAPMの公式

数学的には、CAPMの公式を以下のように定義することができます。

数式：期待リターンの算出

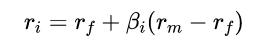
  • ri​ = 資産iの期待収益率 （算出結果＝期待リターン）

  • rf​ = リスクフリーレート（無リスク利子率）

  • rm = 市場の期待収益率

  • βi​ = 資産iのβ（ベータ）係数

なるほど、よくわからんとなるので、いくつか前提となる用語をまとめておきました。

rf = リスクフリーレート（無リスク利子率）

リスクが最小でリスク・フリーに近い金融商品から得られる利回りのことで、「 rf 」と表記されます。
例えば、T-Notes（米国債）の利回り、預貯金による利息などがあります。CAPMはリスクフリーレート＝rf が存在すると仮定して計算を行います。

# リスクフリーレート(サンプルで0.01 = 1%としています。)
risk_free_rate = 0.01

rm = マーケットリターン（市場リターン）

マーケットリターン（市場リターン）は特定の市場における全体的なリターンを示す指標で「rm」と表記されます。代表的なポートフォリオで利用されるケースとして、米国市場であればS&P500というインデックスが該当します。
※S&P500は、米国上場500社の時価総額を加重した指数ですね。

マーケットリターンを取得する関数

def get_index_data(symbol: str, start: str, end: str) -> pd.DataFrame:
     """ SP500 の時系列データ取得 """
     start = datetime.strptime(start, '%Y,%m,%d')
     end = datetime.strptime(end, '%Y,%m,%d')
     df = web.DataReader(symbol, 'stooq', start, end)
     df.sort_index(inplace=True)
     return df

def get_index_return(symbol: str, start: str, end: str) -> pd.Series:
    """ SP500 のリターンの取得 """
    index_data = get_index_data(symbol, start, end)['Close'].pct_change()
    index_data.name = 'Return' # シリーズの名前を'Return'に設定
    return index_data

# SP500のリターンを取得(2020年7月31日～2023年7月31日)
symbol = "^SPX" # シンボルは文字列で指定
market_return = get_index_return(symbol, "2020,7,31", "2023,7,31")

β = ベータ

ベータは資産のリターンが市場全体（S&P500など）と、どの程度の連動性があるかを測定します。例えば、市場リターンが1%増加した場合、資産のリターンがどれぐらい増加するかを、ベータ(β)という尺度ではかります。
CAPMにおいて、システマティック・リスク（市場リスク）と資産の期待リターンとの関係を表すために使用されます。

市場全体のベータは1.0であり、個別銘柄は市場に対するボラティリティの高さでランク付けされ、リスク分析としてリスクの度合いを評価したり、ポートフォリオ戦略として、特定のセクターやリスクプロファイルに合わせてポートフォリオを構築したい場合、ベータ値を用いて銘柄の選定やウェイト調整を行うことが一般的です。

ベータを取得する関数

# 個別銘柄のβを取得
def calculate_beta(stock_return: pd.Series, market_returns: pd.Series) -> float:
    covariance = np.cov(stock_return, market_return)[0][1]
    variance = np.var(market_returns)
    beta = covariance / variance
    return beta

βが1.0の場合、その価格は市場と正相関、つまり市場と同等の連動性であることを意味します。
ベータ＜1.0の場合、「ディフェンシブ」と呼ばれ、理論的にはその証券が市場よりも変動が小さいことを示します＝値動き（リスク）が低い
ベータ＞1.0の場合、「アグレッシブ」と呼ばれ、その資産価格が市場よりも変動が大きいことを示します＝値動き（リスク）が高いとみなします。

複数銘柄の株価リターンを取得

予め株価リターンを計算し、株価リターン（AAPL)を用いて、ベータの算出、CAPMの計算から期待リターンを算出します。
以下のソースコードでは、指定した銘柄リストを作成し、複数の株価リターンを取得できるようにしています。
対象の株価リターンを操作する場合、stocks_returns["AAPL"]のようにして、個別銘柄を指定することができます。

def get_stock_data(symbol: str, start: str, end: str) -> pd.DataFrame:
    start = datetime.strptime(start, '%Y,%m,%d')
    end = datetime.strptime(end, '%Y,%m,%d')
    df = web.DataReader(f"{symbol}.US", 'stooq', start, end)
    df.sort_index(inplace=True)
    return df

def get_stocks_close(symbols: Union[str, list], start: str, end: str) -> pd.DataFrame:
    if isinstance(symbols, str):
        symbols = [symbols]

    stocks = {}
    for symbol in symbols:
        stocks[symbol] = get_stock_data(symbol, start, end)['Close']

    return pd.DataFrame(stocks)

def get_stocks_returns(symbols: list, start: str, end: str) -> pd.DataFrame:
    stocks = {}
    # get_stocks_close を呼び出す時にsymbolsリストを渡す
    closes = get_stocks_close(symbols, start, end)
    for symbol in symbols:
        # 各銘柄のClose価格の取得
        close = closes[symbol]
        # リターンの計算
        stocks[symbol] = close.pct_change() * 100
    
    return pd.concat(stocks, axis=1)

stocks = ["AAPL", "GOOGL", "AMZN", "MSFT"]
stocks_returns = get_stocks_returns(stocks, "2021,7,31", "2023,7,31")
stocks_returns.tail(10)

個別銘柄のベータ

上記の株価リターン(stocks_returns)からデータを取得することができました。続いて、stocks_returns["AAPL"]のリターンデータを用いて、個別銘柄ベータを算出してみましょう。
以下の関数を用いて、AAPLのベータを取得します。

def calculate_beta(asset_returns: pd.Series, market_returns: pd.Series) -> float:
    """ betaの計算 """
    covariance = np.cov(asset_returns, market_returns)[0][1]
    variance = np.var(market_returns)
    beta = covariance / variance
    return beta

stock_return = stocks_returns['AAPL'].dropna()
market_return = market_return.dropna()
beta_aapl = calculate_beta(stock_return, market_return)

print(beta_appl)
>>> 1.33303...

AAPLのβは 1.33303 という計算結果でした。
つまり、市場（SP500）に対して1.33%の変動性があり、市場が1%上昇すればAAPLはおおよそ1.33%上昇することが期待されます。

個別銘柄のCAPM

続いて、AAPLをベースにCAPMフレームワークを用いて、期待収益率を計算してみましょう。先にCAPMを計算する関数を実装しておきます。
この関数は前述した、数式をベースに定義しています。

# CAPMの計算 (リスクフリーレートと市場リターンはサンプルとして設定)
def get_capm(beta: float, market_return: float, risk_free_rate: float) -> float:           """ CAPMを求める """
     return risk_free_rate + beta * (market_return - risk_free_rate)

※CAPMを算出するために、市場(銘柄）の期待収益率の平均とベータ係数を算出する必要があります。

# リスクフリーレート(サンプルで0.01 = 1%)
risk_free_rate = 0.01 

# マーケットリターンの平均を算出
average_market_return = market_return.mean()

# CAPMから期待リターンを算出
expected_return = get_capm(beta, average_market_return, risk_free_rate)
print(expcted_return) 
>>> 0.06318...

期待収益率（expceted_return)は 0.06318 （=6.3%)という結果になりました。単純すぎる内容のため、この銘柄の期待収益率が市場全体やベンチマークと比較してどうか？期待収益率ではなく、その銘柄もつリスク（ボラティリティやβ）も考慮する必要があります。
CAPMはポートフォリオ型のフレームワークの為、複数の銘柄での期待収益率を見てみましょう。

ポートフォリオ型のβ/CAPMの算出

# 各銘柄のウェイト（ここでは25%に等分）
weights = np.array([0.25, 0.25, 0.25, 0.25])
portfolio_return = (stock_return * weights).sum(axis=1)

covariance_portfolio_market = np.cov(portfolio_return, market_return)[0][1]
variance_market = np.var(market_return)

portfolio_beta = covariance_portfolio_market / variance_market
portfolio_expected_return = risk_free_rate + portfolio_beta * (expected_market_return - risk_free_rate)

print("ポートフォリオのベータ値:", portfolio_beta)
print("ポートフォリオのCAPMに基づく期待リターン:", portfolio_expected_return)

ポートフォリオのベータ値: 1.359995…(およそ35.9%)
ポートフォリオのCAPMに基づく期待リターン: 0.105199…(およそ10%)
の期待収益率を算出できました。


理論の提唱者であるハリー・M・マーコウィッツは、この理論を開発する過程で、投資ポートフォリオを効率的に構築する方法を提供しました。個別資産の期待収益率が、無リスク利率と市場ポートフォリオの超過収益に対する感応度（ベータ係数）に基づいて決定されることを前提にしています。

投資家は自分のリスク許容度に応じて、最適なリスクとリターンのバランスを達成したポートフォリオを作成するという、合理的な行動に基づいており、未来の株価を予測するものではありません。
しかし、より高度なアプローチとして、リスクファクターモデルの構築や、投資の選定基準を明確にする最小分散アプローチ、効率的フロンティアの算出など応用的な定量アプローチを目指すことができますね（ひいらぎ）

【C102　東ピ18ab】Starsand Plane 新刊告知

さて、もう明後日になりますが、8/13(日）にコミックマーケット102に参加することになり、最終の準備を行っています。
同人誌の中身は以下の詳細ページにサンプルがありますが、私のパートでは、全体的にプログラミングを主体とした金融のアプローチを中心に執筆しています。
ボリュームが多くなりましたが、上記のように解説とプログラミングをメインにしており、わかりやすい内容を意識しました（あまり小難しい書き方を意識して、例えば話を盛り込んだりして平易な文章にしています）

■詳細ページ
https://www.pixiv.net/artworks/110495832

日時：23年8月13日（日） 東5ホール 東ピ 18ab
サークル名：Starsand Planet
SP本②
A Deep Dive into Financial Landscape.
著者　黒猫アイランド・松崎美子・ひいらぎ

売り子：逢坂みぁさん(https://twitter.com/mia_xqx)
と当日もう一人予定しており、お待ちしております。

台風の動向が気になりますが、天気予報をみてるとだいぶ停滞している模様。。開催中の交通機関等も大丈夫だと思いますが、翌日の新幹線や飛行機など、帰りに影響を受ける方もいらっしゃると思います。天候が変わりやすいので、こまめなチェックをお願いいたします。

また、当日は大変蒸し暑くなっていると思いますので、こまめな水分補給と睡眠など熱中症対策はお願いします。皆さま、どうかお気をつけてお越しください（ひいらぎ@夏バテ）

この記事が気に入ったらサポートをしてみませんか？