
定量分析のはじめかた3
前回の定量分析のはじめかた2の続きとなります。
前回は単一の銘柄について、株価データの取得やグラフを用いた可視化を行いました。今回は複数の構成銘柄からデータを取得し、金融時系列データの分析を行っております。
想定より長くなりましたが、今回もできるだけわかりやすい記載にしていますので、お楽しみいただければ幸いです。早速進めていきましょう。
株価データの取得
前回の記事と同様に、株価データを取得するコードを再利用しています(get_stock_data関数)
今回はさらに、複数の株価を一括取得できるコードを実装し、終値の価格時系列データを一つのデータフレームにまとました(get_stocks_close関数)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import pandas_datareader.data as web
from typing import List, Dict, Any
from datetime import datetime
def get_stock_data(symbol: str, start: str, end: str) -> pd.DataFrame:
""" Stooqから 株価の取得する関数 """
start = datetime.strptime(start, '%Y,%m,%d')
end = datetime.strptime(end, '%Y,%m,%d')
df = web.DataReader(f"{symbol}.US", 'stooq', start, end)
df.sort_index(inplace=True)
return df
def get_stocks_close(symbols: list, start: str, end: str) -> pd.DataFrame:
""" Stooqから複数の銘柄のCloseのみを取得する関数 """
stocks = {}
for symbol in symbols:
stocks[symbol] = get_stock_data(symbol, start, end)['Close']
return pd.concat(stocks, axis=1)以下のコードを実行することで、時系列データを取得することができます。
2行目にあるリストに代表的ITセクター銘柄である["AAPL", "GOOGL", "AMZN", "MSFT"]を指定しました。コード上の銘柄指定は"リスト形式"になっている為、別の銘柄を追加し、株価データを取得することが可能です。
# 以下のリストに銘柄を指定
stocks = ["AAPL", "GOOGL", "AMZN", "MSFT"]
stocks_df = get_stocks_close(stocks, "2023,1,1", "2023,7,21")
stocks_df.tail(10)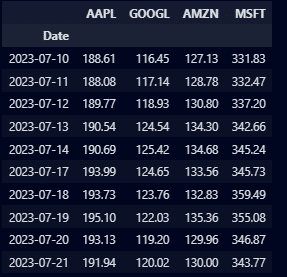
株価リターンの取得
次に株価リターンを取得します。株価リターンは投資対象となる株式の価格変動をパーセンテージで表現したもので、特定の期間におけるトレーディングの収益性を評価することができます。
開始時点(2023/1/1)と終了時点(2023/7/21)の株価を比較し、pct_change()を用いて、価格変動率を算出します。
def get_stocks_returns(symbols: list, start: str, end: str) -> pd.DataFrame:
""" Stooqから複数の銘柄のリターンを取得する関数 """
stocks = {}
for symbol in symbols:
# Close価格の取得
close = get_stock_close(symbol, start, end)['Close']
# リターンの計算
stocks[symbol] = close.pct_change()
# 銘柄ごとのリターンを結合
return pd.concat(stocks, axis=1)
stocks = ["AAPL", "GOOGL", "AMZN", "MSFT"]
stocks_returns = get_stocks_returns(stocks, "2023,1,1", "2023,7,21")
stocks_returns.tail(10)連続する2つの株価間のリターン(変動率)が計算され、新たなデータフレームが生成されました。以下の出力結果が各銘柄ごとの日次リターンとなります。
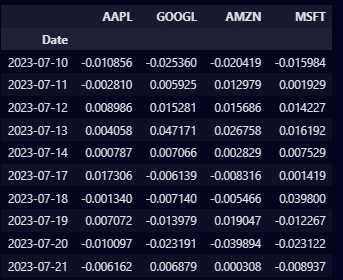
各銘柄の日次リターンを用いて、統計分析やパフォーマンスを評価・分析することができます。
分析を定量的に行うことで、トレーディング戦略の立案や、ポートフォリオのリスク管理の観点から用いられます。まずは簡単に、できることやってみようということで、このデータを使って分析を進めていきましょう。
複数銘柄の累積リターン&グラフによる可視化
累積リターンについては、前回の2でも出てきた内容です。今回は複数銘柄を用いて累積リターンを作成しています。あわせて、グラフにプロットしてみましょう(前回の記事にあった、対数ログリターンは省略しています)
def get_stocks_cumulative_returns(symbols: list, start: str, end: str) -> pd.DataFrame:""
" Stooqから複数の銘柄の累積リターンを取得する関数 """
stocks = {}
for symbol in symbols:
# Close価格の取得
close = get_stock_close(symbol, start, end)['Close']
# リターンの計算
return_ = close.pct_change()
# 累積リターンの計算
stocks[symbol] = (1 + return_).cumprod() - 1
# 銘柄ごとの累積リターンを結合
return pd.concat(stocks, axis=1)
# 構成銘柄を指定
stocks = ["AAPL", "GOOGL", "AMZN", "MSFT"]
stocks_cumulative_returns = get_stocks_cumulative_returns(stocks, "2023,1,1", "2023,7,21")
# データのプロット
plt.figure(figsize=(14,7))
for symbol in stocks_cumulative_returns.columns:
plt.plot(stocks_cumulative_returns.index, stocks_cumulative_returns[symbol], label=symbol)
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.title('Stock Cumulative Returns Over Time')
plt.legend()
plt.grid(True)plt.show()

今年の2023年1月1日から、7月下旬にかけての累積リターンを出力です。
ITセクター銘柄で大きな時価総額を持つ、ビッグテックと呼ばれる銘柄ですが、同じような累積リターンを描いたグラフであることもわかります。
他の銘柄と比較してみると、色んな気づきや変化があるかもしれませんね。銘柄を変更したい場合、コードの stocks = ["AAPL", "GOOGL", "AMZN", "MSFT"]の銘柄名を変更頂くことでデータの取得が可能です。
続いて、基本的な統計的な分析を進めていきましょう。
確率密度関数(PDF:probability density function)
確率密度関数(Probability Density Function, PDF)は、特定の範囲における確率変数値の確率を視覚的に表示する関数です。
つまり、その確率変数がどのように分散(ちらばっているか)しているか、またはどのように一般的な傾向がでているか(=確率が高いか)を表しています。
import seaborn as sns
# ヒストグラムと確率密度関数のプロット
for symbol in stocks_returns.columns:
sns.distplot(stocks_returns[symbol].dropna(), hist=True, kde=True,
bins=int(180/5), label = symbol,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 4})
plt.xlabel('Returns', fontsize=13)
plt.ylabel('Density', fontsize=13)
plt.title('Histogram, PDE of returns', fontsize=15)
plt.legend()
plt.show()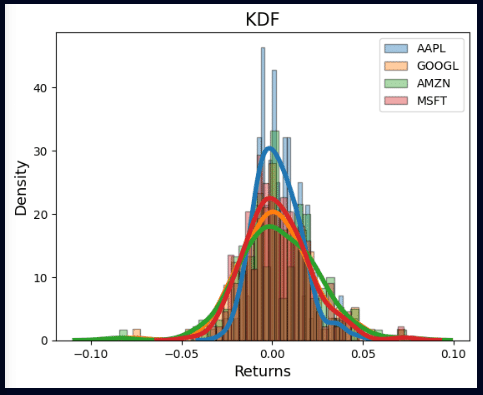
ヒストグラムが重なってしまい見づらくなりましたが、各銘柄の株価リターンの頻度を示しています。正規分布のPDFは、確率変数の相対的な確率を示すことができ、ベル型の曲線で表現されます。
この曲線の面積は常に1=100%となります(すべての可能な結果の確率を合計したものは100%のため)
PDFとヒストグラムと2つのグラフを比較することで、株価リターンが正規分布に従っているかどうか、またはそれからどれだけ逸脱しているかを判断することができます。
カーネル密度推定(KDE:Kernel Density Estimation)
KDEは、データの確率密度関数(PDF)を推定するための非パラメトリックな方法です。データセットが与えられたときに、そのデータがどのように分布しているか、視覚的に把握するために用いられます。
KDEは個々のデータポイントを、中心がそのデータポイントであるような「カーネル」(滑らかなピークがあるような関数)で置き換え、全てのカーネルを足し合わせて、中心が尖った滑らかな曲線を形成します。その結果がデータの確率密度関数の推定値となります(ざっくりですが。。)
# KDEをプロット
sns.kdeplot(stocks_returns, label='IBM')
plt.xlabel('Returns')
plt.ylabel('Density')
plt.title('KDE of returns')
plt.show()
KDEはヒストグラムよりも滑らかな分布を生成するため、データの特徴をより直感的に理解するのに使われています。ただし、KDEの精度はカーネルの選択とカーネルの幅(バンド幅)の設定に依存しますし、一つの統計指標をはかる目安としてお考えください。
4分位の計算
4分位数(しぶんいすう:Quartiles)とは、データセットを四等分するための値で、以下の3つの点からなります。25%(第一四分位)、50%(第二四分位または中央値)、75%(第三四分位)の値を示しており、4分位数はデータのばらつきや偏りを理解するために使われます。
先ほどの株価リターン(stocks_returns)を用いて、4分位数を計算し、データフレームに格納しています。
def calculate_quartiles(stocks_returns: DataFrame) -> DataFrame:
""" 四分位数の計算 """
# 空のデータフレームを作成
quartiles_df = DataFrame()
# 各銘柄について四分位数を計算し、データフレームに追加
for symbol in stocks_returns.columns:
quartiles = stocks_returns[symbol].quantile([0.25, 0.5, 0.75])
quartiles_df[symbol] = quartiles
return quartiles_df
quartiles_df = calculate_quartiles(stocks_returns)
quartiles_df
ボックスプットの作成
ボックスプロット(箱ひげ図)はデータの分布を視覚化するツールです。
データの分布、中央値、データのばらつき、そしてアウトライヤー(外れ値)を視覚的に理解することが可能です。ボックスプロットは以下の条件で構成されています。
・ボックスの下辺(Q1)
・ボックスの上辺(Q3)
・ボックスの内部の線(中央値)
・下のひげ:Q1から1.5倍の四分位範囲(IQR:Q3 - Q1)下へ延びた線
・上のひげ:Q3から1.5倍の四分位範囲(IQR:Q3 - Q1)上へ延びた線
・ボックス外の点(外れ値)
# ボックスプロットの作成
plt.figure(figsize=(10,7))
sns.boxplot(data=stocks_returns)
plt.xlabel('Stocks', fontsize=12)
plt.ylabel('Returns', fontsize=12)
plt.title('Boxplot of return', fontsize=15)
plt.show()ボックスプロットを可視化してみましょう。

"箱"の部分の説明です。
データの中央50%を視覚化しています。箱の下端は第1四分位数(Q1)を示し、データの最小値から中央値までの中間地点、このラインより下にあるデータは下位25%に位置しています。
箱の上端は第3四分位数(Q3)を示し、データの中央値から最大値までの中間地点、このラインより上にあるデータは上位25%に位置しています。
箱の中央に描かれた線は中央値(または第2四分位数)を示しており、データを小さい順に並べた場合のちょうど真ん中の値になります。
次に、"ひげ"の部分の説明です。
ひげは、箱の上下に描かれ、データの変動性を示しています。
下のひげは、Q1から1.5倍の四分位範囲(Q3 - Q1)を引いた値までを示しています。上のひげは、Q3から1.5倍の四分位範囲(Q3 - Q1)を足した値までを示しています。この1.5倍の四分位範囲(Q3 - Q1)は、データの大部分が含まれる領域です。
最後に、ボックス外の点です。これらは一般的にアウトライヤー(外れ値)と呼ばれ、通常の範囲(Q1からQ3まで、またはひげの範囲)を大きく超えた値または下回った値を表しています。これらの点は、異常値やデータの分散が大きいことを示しています。
分散と標準偏差
金融市場は不確実性の観点からも、様々な要因に影響を受けます。結果的に、価格やリターンには大きな散らばりが生じることがあります。その変動の度合いを知るために、「分散」と「標準偏差」という2つの指標が使われます。
分散や標準偏差のデータそのものが、直接的に何かを示すわけではありませんが、各データを上手く使うことで投資のリスクやパフォーマンスを計測することができます。
「分散」は、データのばらつきの度合いを示す指標で、値が大きいほどデータのばらつきが大きいことを示します。しかし、分散の値は元のデータの二乗単位で表されるため、直感的に理解しにくいですね。
そこで、「標準偏差」が使われます。分散から平方根をとったもので、元のデータと同じ単位で表示されるので、理解しやすくなります。
リターンの標準偏差が大きい銘柄ほど、その銘柄の価格変動が大きいと言えます。リスクを計測して把握することが可能になります。リスクの高い投資とリスクの低い投資を明確に区別でき、トレーダー自身のリスク許容度に合わせたトレードが選択可能となります。
stats_df = pd.DataFrame({"Variance": variances, "Standard Deviation": std_devs})
stats_df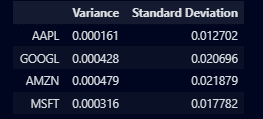
※分散と標準偏差を使ったテーマは、次のnoteで記載する予定です。
相関行列(相関分析)
相関行列は、複数の株価の関連性をマッピングして把握するツールです。銘柄の関連性を視覚的に理解し、投資リスクを管理し、統計的評価を行うことができるようになります。
統計的分析において、多重共線性(マルチコともいいます)を確認するのに役立ちます。異なる変数間で強い相関が見られる場合、それらの変数から得られる情報が重複している可能性があり、統計的推定が不安定になる可能性かもしれませんね。
# 相関行列のヒートマップを作成
plt.figure(figsize=(12, 9))
sns.heatmap(corr_matrix, annot=True, cmap='viridis', vmin=-1, vmax=1)
plt.title('Correlation Heatmap')
plt.show()
相関分析はポートフォリオの設計でも大事な役割を果たします。異なる銘柄の動きが密接に連動している場合、リスク分散することは難しくなります。しかし、各銘柄間の相関性を理解し、銘柄群の時系列データの変動を分析することで、ポートフォリオ全体のリスクを減らすことが可能になります。
(もちろん、相関についての概念なども理解する必要がありますが、この辺の内容も同人誌ではもう少し掘り下げて記載しています)
ポートフォリオの作成
ポートフォリオの標準偏差とリターンを計算する内容です。
当記事を終わりにしたいと思います。ポートフォリオは先ほど、指定した4つの銘柄のリターンから作成しています。
from typing import Tuple
def portfolio_analysis(stocks_returns: pd.DataFrame, portfolio_weights: np.ndarray) -> Tuple[float, pd.Series]:
""" ポートフォリオの標準偏差とリターンを計算する関数 """
# 重み付けされたリターンポートフォリオを作成
weighted_returns_portfolio = stocks_returns.mul(portfolio_weights, axis=1)
stocks_returns['Portfolio'] = weighted_returns_portfolio.sum(axis=1)
# 株とポートフォリオの共分散を計算
stocks_covariance = stocks_returns.cov()
annualized_covariance = stocks_covariance * 252
annualized_covariance = annualized_covariance.loc[['AAPL', 'GOOGL', 'AMZN', 'MSFT'], ['AAPL', 'GOOGL', 'AMZN', 'MSFT']]
# ポートフォリオの標準偏差を求める
portfolio_sd = np.sqrt(np.dot(portfolio_weights.T, np.dot(annualized_covariance, portfolio_weights)))
return portfolio_sd, stocks_returns['Portfolio']# ポートフォリオウェイトを均等にする
portfolio_weights = np.array([0.25, 0.25, 0.25, 0.25])
portfolio_sd, portfolio = portfolio_analysis(stocks_returns, portfolio_weights)
print(f"Portfolio standard deviation: {portfolio_sd}")
print(f"Portfolio returns:\n{portfolio}")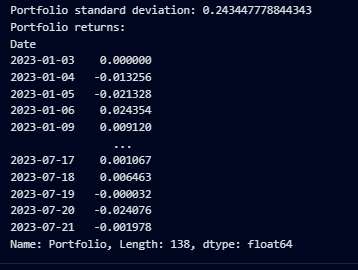
最終的なポートフォリオの結果
数字みても何もわからん。。というところで、最後は可視化をして終わりたいと思います。累積データを単純にプロットを書くことで、表示することができますが、グラデーションにより少し装飾をしてみました。
import matplotlib.collections as mcoll
import matplotlib.path as mpath
def colorline(x, y, z=None, cmap='viridis', norm=plt.Normalize(0.0, 1.0), linewidth=3, alpha=1.0):
"""
http://nbviewer.ipython.org/github/dpsanders/matplotlib-examples/blob/master/colorline.ipynb
http://matplotlib.org/examples/pylab_examples/multicolored_line.html
"""
# デフォルトの色は[0,1]に等間隔に配置
if z is None:
z = np.linspace(0.0, 1.0, len(x))
# 数字が1つの場合の特殊ケース
if not hasattr(z, "__iter__"): # to check for numerical input -- this is a hack
z = np.array([z])
z = np.asarray(z)
segments = make_segments(x, y)
lc = mcoll.LineCollection(segments, array=z, cmap=cmap, norm=norm, linewidth=linewidth, alpha=alpha)
return lc
def make_segments(x, y):
""" x座標とy座標から線分のリストを作成 """
points = np.array([x, y]).T.reshape(-1, 1, 2)
segments = np.concatenate([points[:-1], points[1:]], axis=1)
return segments
fig, ax = plt.subplots()
# カラーマップの生成
lc = colorline(range(len(portfolio_cumulative)), portfolio_cumulative.values, cmap='viridis')
ax.add_collection(lc)
ax.set_xlim(0, len(portfolio_cumulative))
ax.set_ylim(portfolio_cumulative.min(), portfolio_cumulative.max())
plt.xlabel('Date')
plt.ylabel('Cumulative Return')
plt.title('Portfolio Cumulative Return with Gradient')
plt.show()
累積リターンはおよそ1.5(50%)、つまり、2023/1/1から7月下旬にかけて、4つの銘柄を保有していれば、そういったリターンが見込めたということがわかります。一定の比重からポートフォリオを構成し、ポートフォリオリターンを計算することも行いました。
定量分析のはじめかた1でも取り扱いましたが、シャープレシオやドローダウンなどを分析することで、ご自身が持つポートフォリオの構成銘柄のパフォーマンス評価を知る土台が整いました。
次回よりポートフォリオの内容を掘り下げて、CAPM(資本資産価格モデル)などのフレームワークなどを記載する予定です。
トレーディングの分析の参考に役立てて頂ければ幸いです(ひいらぎ)
