
機械学習の勉強Part2: HDBSCAN
イキサツ
前回の記事同様,ノンパラメトリックベイズを理解しつつ,周辺知識をつけるために今回は,HDBSCANについて勉強していきます.
論文のURLを張っておきます.
また,下記の記事も参考にしております.
ちなみに,以下が前回記事になっているのでよろしければ見て行ってあげてください.
また,今回からChatGPTとNotion AIをお供に連れて,記事を書いていきます.
概要
HDBSCANは密度ベースのクラスタリングアルゴリズムであり,Hierarchical Density-Based Spatial Clustering of Applications with Noiseの略称になります.密度ベースクラスタリングというのは,簡単に言うとデータの集まり(密度)を距離で区切ってクラスタに分割する手法です.
このHDBSCANは,その密度ベースクラスタリングの中でもめちゃめちゃ優秀・有名なDBSCANの発展形で、階層構造(Hierarchical)を持つ手法です.
キーワードは,距離,階層構造+DBSCANです.
理論解説
HDBSCANでは,大別すると階層型クラスタリング→階層の圧縮→信頼性の評価の3ステップで行われます.肝となるのは階層型クラスタリングの距離の定義と信頼性の評価に基づくクラスタの抽出になります(まぁ,肝といえば全部肝ですが… ).
このため,上記二つは丁寧に説明していきます.
階層型クラスタリング
階層型クラスタリングはデータを木構造で表現することで、クラスタの階層構造を表現する手法です.この手法には凝集型(ボトムアップ)と分割型(トップダウン)の2つのアプローチがあります.凝集型クラスタリングは全てのデータにクラスタを一度振り分け,最も近いクラスタから順に統合していき,最終的に一つのクラスタにまとめる手法になります.一方、分割型クラスタリングは全てのデータを1つのクラスタとみなし,そこからデータを分割していき最終的に個々のデータを含むクラスタを得る手法になります.
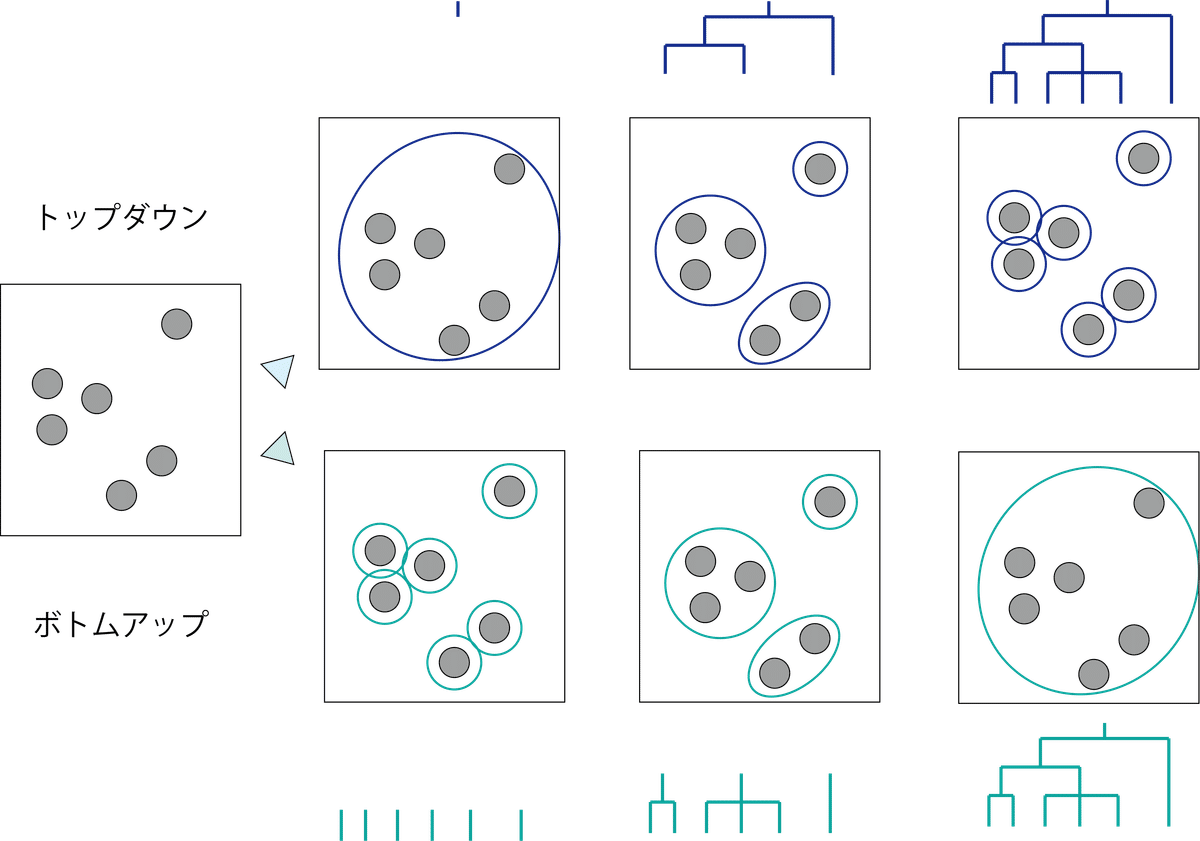
階層型クラスタリングでは,圧倒的にボトムアップの方が扱いやすく分かりやすいです.トップダウンの場合,分割のパターンがいくつも存在するため計算量が爆発的に増えるなどの懸念があります.ボトムアップの場合は,一番近いクラスタをくっつけてあげるだけなので,比較的容易にできます.このため,ボトムアップのクラスタリング手法がよく使われます.
HDBSCANではボトムアップの最短距離法が使われています.ここ手法は正直,何でもいいと思われますので簡単に説明していきます.
この最短距離は,各クラスタにおいて一番近接しているデータを持っているクラスタを統合します.このため,クラスタ内のデータ同士の距離を全て算出し,その中で一番距離の小さな組合せをクラスタ間距離に換算します.このクラスタ間距離は平均値とかでも代用可能です.

HDBSCANではこの距離の算出に相互到達距離という概念が登場します.これは対象の点の周りの密度を考慮した距離になります.下記が論文内での式です.

上式は点aと点b間の距離を計算するもので,点aのコア距離 or 点bのコア距離 or 点aと点bのユークリッド距離の中で最大のものを選ぶ内容となってます.ここで,コア距離(core k)ですが対象の点を中心として,k個目のデータが円内に入るまでの距離を指します.下図がわかりやすいかと.

上図はk=3としているため,どちらの半径も3個目のデータに到達したところが半径になっています.このkの値を変えることで,データの密度に合わせた距離設定ができます.kの値に対して密度が大きければ,ユークリッド距離が,密度が小さければどちらかのコア距離が採用される形になります.
ちなみに,この場合の相互到達距離はユークリッド距離d(a,b)になります.
樹形図の圧縮
前章ではHDBSCANで用いられる距離の概念とそれを使った階層型クラスタリングについて解説しました.続いては,前章のクラスタリングで構築した樹形図を圧縮します.例えば,下図のような樹形図がクラスタリングによって得られたします.
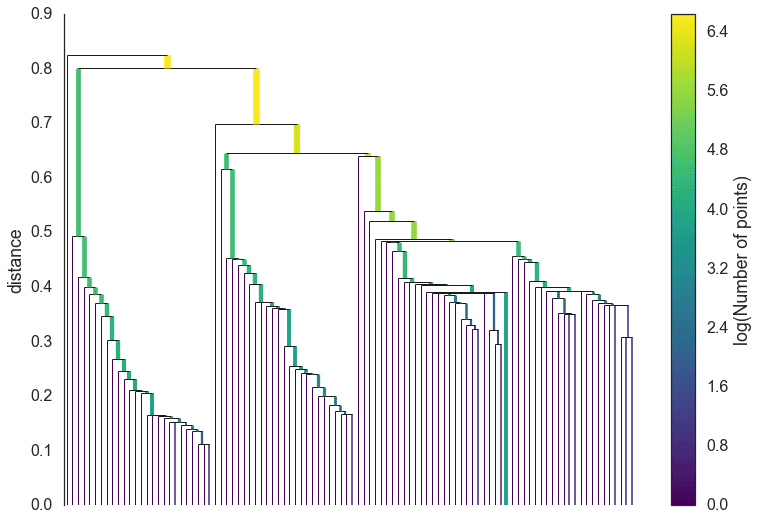
階層型クラスタリングでは,樹形図の生成後にどこまでをクラスタとするかといった閾値の設定が必要になります.上図を直感的に区切るのであれば,私だったらdistanceが0.6~0.7のいずれを選びますね
一方,形や分岐が複雑であったりする場合,樹形図をもう少し簡素化したいと考えます.そこで,最少クラスタサイズを決めて,このサイズ以下なら枝切りと統合を行います.
ここで,ある(親)クラスタの分岐において,下記のことが考えられます.
分岐する2つの(子)クラスタが最小サイズ以上
分岐する2つの(子)クラスタの片方が最小サイズ以上
分岐する2つの(子)クラスタの両方が最小サイズ以下
1の場合なら,親クラスタは真クラスタと判定し,樹形図的には何もしません.2の場合なら,最小サイズ以下の子クラスタをカットし,残った子クラスタを親クラスタに統合します.3は両方カットして終了ですね.これの操作を繰り返し行ったのが下図になります.

大分,見やすい樹形図になりましたね! ちなみに,縦軸のλは1 / distanceになってます.このとき,各クラスタの面積の広いところがクラスタとして優秀です.今回は面積算出まで書くとややこしくなるので,そこは省いてクラスタの選出について書きます.
クラスタの抽出
クラスタの最適化では,圧縮した樹形図の親クラスタ vs 子クラスタを全てに操作していき,残ったものを抽出します.まずは,下図のような樹形図と面積が与えられるとします.

この図の場合だと,色づいている箇所が最適なクラスタになります.
最適化の操作は割と簡単で,一番下のクラスタ(C10, C11)から親クラスタ(C8)の値が子クラスタ(C10, C11)の値の和より大きいかの判定を行います.操作は以下のことを繰り返します.
全てのノードにフラグ(1)を付与
親クラスタ < 子クラスタ1 + 子クラスタ2 なら親クラスタ = 子クラスタ1 + 子クラスタ2とし,親クラスタのフラグを0
親クラスタ >= 子クラスタ1 + 子クラスタ2なら,親クラスタ以下のフラグを全て0
上記を繰り返すことで,最適化が行われます.フラグが1のままのノード選択することで,最適なクラスタが選択できます.上図で試してみましょう.
まず,一番下のC10とC11からですね.C8<C10+C11となっているので,C8のフラグを0,C8=C10+C11にします.続いて,C5 > C9+C10+C11となっているので,C5の下のノードのフラグが全部0になります.また,上に行くとC2<C4+C5なので,C2のフラグが0となり,左側のノードはC4とC5のみフラグが1です.
右側も同様に行っていきます.C3>C6+C7となるので,C6とC7のフラグが0となり,最終的にC3,C4,C5がクラスタとして選出され,この3つのクラスタの総和が一番大きい面積となります(他の組み合わせだと最大にならない).
プログラム
HDBSCANの大枠のクラスタリングの仕方がわかったのでプログラムに移ります.今回はプログラムが若干複雑になるため,ライブラリを使って試していきます.
import numpy as np
import matplotlib.pyplot as plt
import hdbscan as hdb
import seaborn as sns
fileName = 'verificationData.csv'
data = np.loadtxt(fileName, delimiter=',')
# hdbscan
h = hdb.HDBSCAN(min_cluster_size=10,min_samples=10, prediction_data=True)
h.fit(data)
labels = h.labels_
# 結果をプロット
fig = plt.figure(figsize=(10, 10))
sns.scatterplot(data[:,0], data[:,1], hue=["cluster-{}".format(x) for x in labels])とても,シンプルですね.データを読み込んで,HDBSCANを学習させて,結果をプロットしてるだけです.以下が結果になります.

きれいに分類されていることがわかります.また,大きな外れ値も検知できるため,クラスタ数を獲得しながら異常検知もできます(すごい!).
一方,HDBSCANは重なっている分布に対して若干弱い性質をもつので,何でもかんでもクラスタリングできるわけではありません.また,パラメータであるmin_cluster_sizeやmin_samplesなどの調整が必要になります.
まとめ
今回は自分の勉強ついでに,HDBSCANについて書きました.詳しいことやもっと理論的なことは論文をお読みください.また,途中で出てくる階層型クラスタリングの図の樹形図ですが,若干の嘘をはらんでおります(鋭い人はお気づきだと思います).申し訳ございません.修正が面倒でそのままにしておりますが,手法の理解という観点であれば大した問題じゃないと判断いたしました.ご容赦ください.
多少,時間をかけて書いておりますので,スキボタンやシェアしていただければ幸いです.また,読者の皆様のお役に立てればよりうれしいです.
