三角形の秘密

今回はちょっとだけまともなお話。

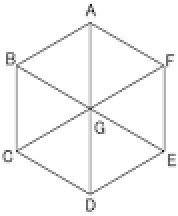
一辺の長さがaの正六角形の面積を求めようというものです。

話を始めやすいように既に一部対角線を引いてあります。
この対角線を引いた状態、同じ三角形が6つくっついてできた状態には…見えないでしょうか？
実は正六角形というのは正三角形を6つくっつけた形であり(証明は省きます)、一辺の長さがaの正三角形の面積を求めることができれば、それを6倍したものが「一辺の長さがaの正六角形の面積」ということになるのです。

では、正三角形の面積を求めてみましょう。

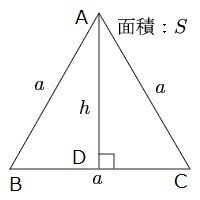
三角形の面積を求めるには、(底辺)×(高さ)÷2
底辺はaなので、hを求めればいいわけですね。
△ABDと△ACDは合同なので、BD = CD =a/2 です(証明省く)。
ここで、△ABDについて三平方の定理を考えます。
(a/2)^2 + h^2 = a^2
h^2 = a^2 - a/4
h^2 = 3a^2/4
h = a√3/2
なので、正三角形ABCの面積は、
a × a√3/2 ÷ 2 = a^2√3/4　
ということになります。
よって、先述のとおり正六角形の面積は、
a^2√3/4 × 6 = 3a^2√3/2

というのをここでは省いた証明も交えて、穴埋め形式でテストの問題に出したりしていました。
なんとか頑張ってセンター試験のような方式にして出題していた(マークではありませんが)ことから、問題に慣れられたと好評を受けていました。

この次に、
一辺の長さがaの正四角形の面積を求めなさい。

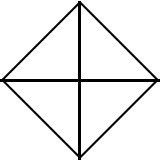
という問題をサラっと出すと、生徒の半数が4つの三角形の面積を求める式などを頑張って書いていました。
ただの正方形だから、a^2 とだけ書けば僅か1秒で正解だというのに。
これをテストを返して解説の時に話すとものすごい不評を受けました。
何故だ…