
マンキュー マクロ経済学I 入門篇(第4版) 勉強会メモ(章末問題)
おことわり
本noteは、『マンキュー マクロ経済学I 入門篇(第4版)』を読みながら書いていく学習メモです。経済学初学者である筆者(ひよっこ)の独習がベースなので、間違っている部分もあるかもしれません。「ここ違うでしょ」と気付かれた詳しい方はこっそり教えてください。
なぜ本noteを公開するのかについて少し説明します(飛ばしてOK)。端的に書くと、「大学に通うことができない(=誰とも輪読できず導いてくれる人もいない)状況の学習者が詰んでしまう」ことが予想されたからです。
Amazonのレビューなどを見ていても、「解答、解説がないので初学者には厳しい」というような批判が見受けられます。せっかくマクロ経済学に興味を持って、そこそこ高額な本を買って、人生の貴重な時間を突っ込んで、でも章末について自分の考えが合っているか全然わかりません、という状況はあまりにも辛いのではないでしょうか。
しかし、それ以外の点において非常に素晴らしい教材であることも事実です。ともすれば数式ばかりに偏りがちな経済学の基礎を、なるべく平易な言葉で、コラムやケーススタディを交えながらしっかり解説してくれる、まさに初学者にうってつけの書物だと読みながら感じています。(雰囲気を知りたい人はgoogle booksのプレビューなどを見てみてください)
このような良書が、ただ独習に向いていないというだけで埋もれてしまうのはもったいないし、もっと多くの経済学に関心のある人に読んでほしい。そう思ったのが公開のきっかけです。
(ものすごく労力がかかるので、私がやらなかったら誰も(無償で)やらないだろうなという思いもありました。無償が偉いという話ではなく、学問ってもっと万人に開かれていた方がいいんじゃないかなーみたいな話です。)
まとめ:マンキューはいいぞ! みんな読もう!
↑ アフィリンクです。回避したい人はご自身で検索してください。
google booksのプレビュー(書籍の雰囲気をつかみたい人用)
訂正情報(入手するバージョンによっては細かい誤植があります)
第一部 イントロダクション
第一章 科学としてのマクロ経済学
復習問題
1)マクロ経済学とミクロ経済学の違いを説明しなさい。この2つの分野はどのように関係しあうか。
扱う対象が異なる。ミクロ経済学は諸企業と諸個人がどのように意思決定を行い、どのように影響し合うのかについての学問であるのに対し、マクロ経済学は、所得や物価、失業率など、経済全体を扱う学問である。
多数の個別主体の決定が総合されたものが集計データとなる。全てのマクロ経済モデルは、ミクロ経済学的基礎を前提としており、矛盾するものであってはならない。
2)経済学者はなぜモデルを作るのか。
現実を単純化することで本質とは無関係な変数を除外し、重要な諸関係に焦点を合わせるため。
3)市場清算モデルとは何か。市場清算の仮定はどのような場合に妥当か。
あらゆる財やサービスの価格が、需要と供給が均衡する点に瞬時に動くことを仮定したモデル。
あらゆる賃金や価格が伸縮的であると仮定した場合。
応用問題
1)最近のニュースのなかから3つのマクロ経済問題を挙げなさい。
FF Rate、The Merge、エルサルバドルがBTCを法定通貨にしました、etc.
2)科学を定義づける性質が何か考えなさい。マクロ経済学は科学と呼ばれるべきだとあなたは考えるか。賛成又は反対の理由を述べなさい。
客観的観察の積み重ね。定義上呼べる。(マンキュー的には経済学は社会科学)
3)需要と供給のモデルを用いて、フローズン・ヨーグルトの価格の下落がアイスクリームの価格とアイスクリームの販売量にどのような影響を与えるか説明しなさい。説明する際に、外生変数と内生変数を明確に区別しなさい。
外生変数:フローズン・ヨーグルトの価格
内生変数:アイスクリームの価格、アイスクリームの販売量
総所得が一定だと仮定すると、フローズン・ヨーグルトの価格が下がることでフローズン・ヨーグルトの需要は増える。アイスクリームの需要は減り(=アイスクリームの販売量は落ち)、アイスクリームの価格も下がる。
4)あなたが散髪に支払う料金はどのくらいの頻度で変更されるか。あなたの答えは、散髪の市場を分析する市場清算モデルの有用性にとって何を意味するか。
たぶん教科書的には「価格って硬直的だと思われてるけど長期で見ると伸縮的だと見なしていいから市場清算モデルは有効だよね」と言わせたいのだと思いますが、いい設問だと思えなかったので、カット代の価格推移を調べてみました。

個人の価格行動や価格認識は置いておいて、市場清算モデルの観点で、カット代の市場は割と伸縮的であることがわかりました。
第二章 マクロ経済学のデータ
復習問題
1)GDPが測定しているものを2つあげなさい。どのようにして、GDPはその2つを同時に測ることができるのだろうか。
総所得・総支出
会計上、買い手の支出は売り手にとっての所得であり、両者は等しい。
2)GDPの4つの構成要素は何か。それぞれの具体例をあげなさい。
消費・投資・政府購入・純輸出
パン・家・道路・自動車
3)消費者物価指数(CPI)は何を測る尺度か。CPIが、GDPデフレーターと異なる3つのポイントをあげなさい。
CPIは基準時点対比の一般物価水準を測る尺度。
① GDPデフレーターは一定の期間内に経済の中で生産された「全ての」最終財・サービスの市場価値を対象とし、CPIは家計(消費者)が購入した財・サービスのみを対象とする。企業や政府の購入はGDPデフレーターには反映されるが、CPIには反映されない。
② GDPデフレーターは国内で生産された財のみを対象とし、CPIは国内で購入された財を対象とする。日本で製造されてアメリカで購入された商品はGDPデフレーターには反映されず、CPIには反映される。
③ GDPデフレーターはGDP構成の変化に対応してバスケットが可変となるが、CPIは固定されたバスケットを用いる。GDPデフレーターはパーシェ指数、CPIはラスパイレス指数を採用している。パーシェ指数は「比較時点の数量ウェイト」、ラスパイレス指数は「基準時点の数量ウェイト」で加重平均を行うため、前者はインフレを過小評価しがちとなり、後者はインフレを過大評価しがちとなる。
4)CPIとPCEデフレーターとの共通点と相違点を説明しなさい。
PCEデフレーターは、GDPの個人消費部分のみを扱う。
(共通点)企業や政府の購入を含まず、消費者が購入する財・サービスの価格のみを扱う点。また、輸入財の価格も含む点。
(相違点)PCEデフレーターでは、消費者支出の構成変化に応じた財のバスケットの経時変化を許容しているが、CPIでは構成が一定である。
5)労働統計局が一国の経済の人々を分類する3つのカテゴリーを述べなさい。失業率の計算方法も説明しなさい。
就業者・失業者・非労働力
就業者:
働いている人。または、休暇・病気・悪天候などの理由で一時的に休んでいる人。
失業者:
働くことが可能で、求職していたが雇用されていない人。または、一時帰休中で、職に戻るのを待っている人。
非労働力:
上記のカテゴリーに入らない人。フルタイムの学生・主婦(夫)・引退者。
労働力人口 = 就業者数 + 失業者数
失業率 = 失業者数 / 労働力人口 *100
6)労働統計局が総雇用を測定するために用いる2つの方法を説明しなさい。
① 家計調査
自分が働いていると答える人数の推定値を得る。
② 事業所調査
自社が雇っていると答える人数の推定値を得る。
これらには相違が発生する。理由は以下の2点
a)それぞれは異なるものを測っている
家計調査では自営業者を雇用者としてカウントするが、事業所調査ではカウントされない(企業が給料を払う対象ではないため)。また、兼業は家計調査では1カウントとなるが、事業所調査では2カウントとなる。
b)調査の不完全性
新規事業者が調査時点で対象に含まれないことがある。また、新規事業者推定モデルや、調査対象の家計の結果を全体に拡張するモデルには誤差がある可能性がある(合法・非合法移民の存在などにより人口の推定値にも誤差が生じる)。
応用問題
1)BEAのウェブサイトを訪ねて、最近の四半期における実質GDP成長率を見つけなさい。BLSのウェブサイトを訪ねて、昨年のインフレ率と最近の(月次)失業率を見つけなさい。それらのデータをどのように解釈するか。
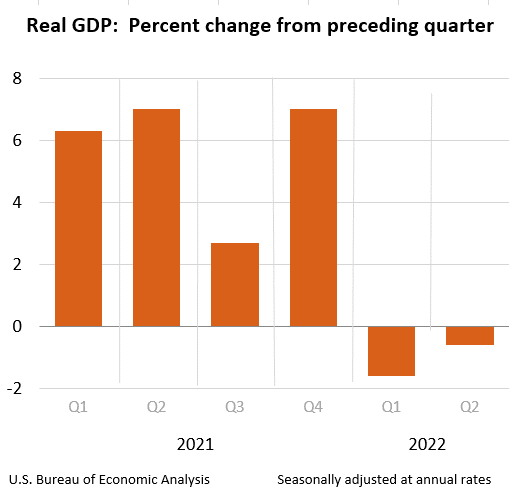

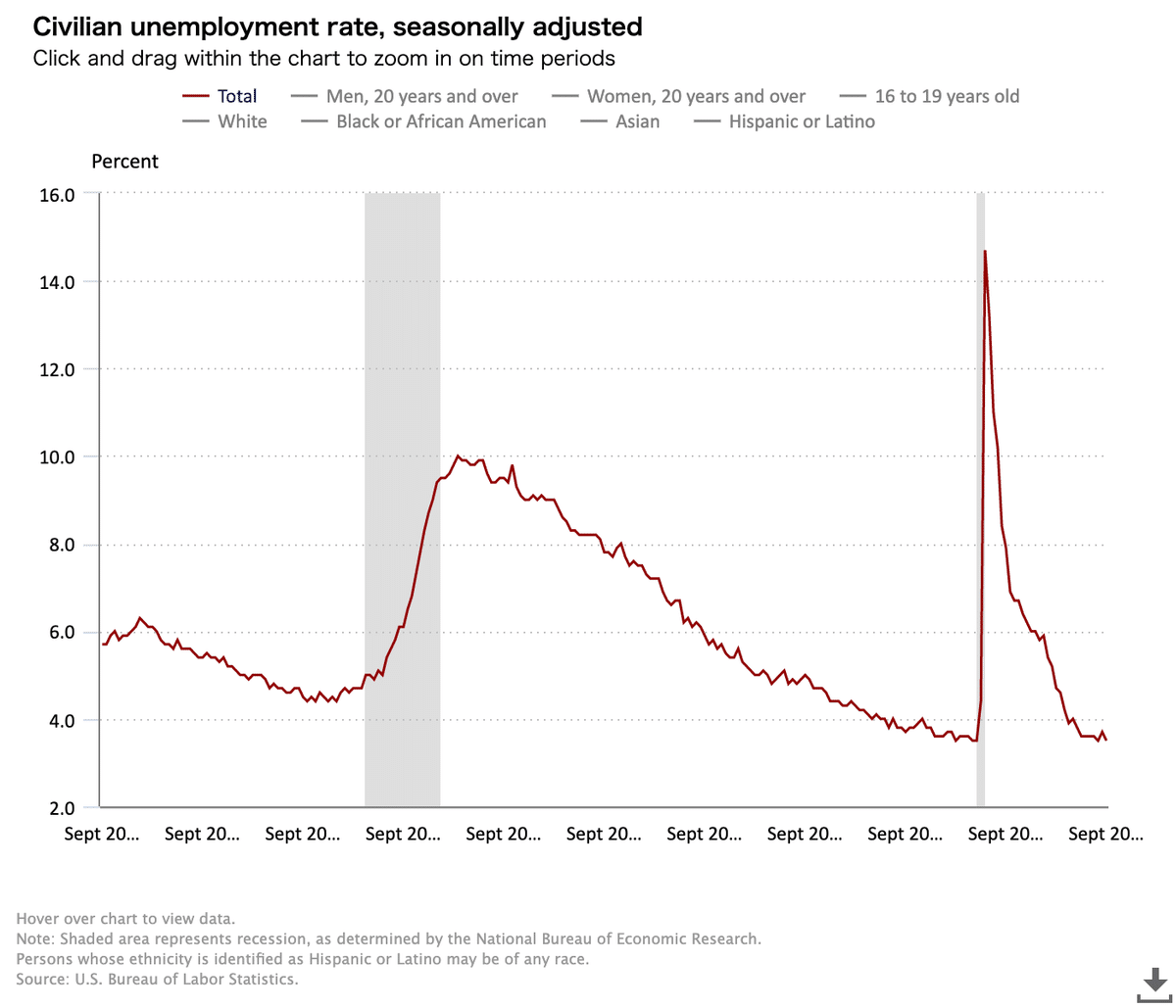
量的緩和政策の終了が2021年12月17日であり、以降は利上げやQT、コロナによる運輸停滞・供給制約などを受け、生産が減少しているのではないか。一方、ほぼコロナ前水準へと復帰したとも言える強い雇用に支えられ、消費は堅調で、CPIは高止まりしており、供給制約が解消されるにつれてGDPの減少幅は縮小し始めたように見える。
2)農家が小麦1ブッシェルを生産して製粉業者に1ドルで販売した。製粉業者は小麦を小麦粉にしてパン屋に3ドルで販売した。パン屋は小麦粉を使ってパンを焼き、エンジニアに6ドルで売った。エンジニアはそのパンを食べた。この取引に関係した人それぞれによる付加価値を求めなさい。パンのGDPへの貢献はどれだけか。
(付加価値)
農家:1ドル
製粉業社:2ドル(3-1)
パン屋:3ドル(6-3)
エンジニア:0ドル
(GDP)
6ドル(1+2+3 or 0+0+6)
3)ある女性が彼女の執事と結婚したとしよう。結婚後も彼女の夫はこれまでどおり彼女に仕え、彼女もこれまでどおり(ただし賃金ではなく夫への贈与として)彼にお金を支払ったとしよう。この結婚はGDPにどのような影響を与えるだろうか。また、どう影響すべきと考えるか。
執事への賃金は有給のサービスであり、これはGDPにカウントされる。しかし、無給の家事+贈与の組み合わせはGDPにはカウントされない。したがって、実質的に同じ行為だったとしてもGDPは減少する。
どう影響すべきと考えるか:そのままでいい気がする。
4)以下の取引はそれぞれ、(アメリカの国民所得勘定の)支出の4項目➖➖消費、投資、政府購入、純輸出➖➖のどれに分類されるか。
a ボーイング社が空軍に航空機を販売した。
b ボーイング社がアメリカン航空に航空機を販売した。
c ボーイング社がエール・フランス社に航空機を販売した。
d ボーイング社がアミリア・エアハート女史(アメリカの女性飛行家)に航空機を販売した。
e ボーイング社が翌年に販売するために航空機を製造した。
a 政府購入
b 投資(企業固定投資)
c 純輸出
d 消費
e 投資(在庫投資)
5)GDPとその構成要素のデータを入手して、以下の各構成要素が1950年、1980年、計算可能な最近年の各年にGDPのどれだけの比率を占めていたかを計算しなさい。
a 個人消費支出
b 民間国内粗投資
c 政府購入
d 純輸出
e 国防支出
f 輸入
データの間に何か安定的な関係はみられるか。何か趨勢的な変化はみられるか(ヒント:データについては、アメリカの場合は経済分析局のウェブサイト〈https://www.bea.gov/〉、日本の場合は『国民経済計算年報』をみるとよい(内閣府のウェブサイト〈https://www.cao.go.jp/index.html〉も参照))。
(1950年)
a 63.3%
b 12.5%
c 26.8%
d 2.7%
e 不明
f 3.4%
(1980年)
a 62.9%
b 12.8%
c 25.6%
d 6.0%
e 不明
f 6.0%
(2021年)
a 70.1%
b 18.4%
c 17.5%
d 12.1%
e 4.0%
f 18.4%
・GDPの母数は基本的に増大している
・個人消費支出は常に最大、輸出入の割合は増加傾向、特に輸入が顕著
・時間的に1950/80年の国防費については別のサイトを当たらなかったが、国防費を入れさせたかった意味はGDP対比では下がっているという観察をさせたいからだと思う(参考)
6)ティナは、ティナの芝刈り(TLM)社の唯一の所有者である。ある年に、TLM社は顧客の芝刈りによって、100万ドルを受け取った。TLM社の機械装置は、消耗によって12万5千ドルだけ減価した。TLM社は、雇用者に60万ドルを支払っており、雇用社は14万ドルを所得税として支払った。TLM社は、5万ドルを法人所得税として支払い、ティナは15万ドルを配当として支払った。TLM社は、企業収益のうち7万5千ドルを将来的な拡大のために、内部留保している。以上の経済活動は、下記のそれぞれの項目に対して、どれだけ貢献したか。
a GDP
b NNP
c 国民所得
d 雇用者の報酬
e 資産保有者の所得
f 企業利潤
g 個人所得
h 個人可処分所得

a 100
b 国民純生産 = 国民総生産 - 減価償却 = 100-12.5 = 87.5
c NNP -(間接税 - 補助金) = 87.5
d 60
e 15
f 法人税 + 配当 + 内部留保 = 5 + 15 + 7.5 = 27.5
g-1 国民所得 -法人企業利潤 + 配当 = 87.5 - 27.5 + 15 = 65
g-2 60 + 15 = 75
h-1 個人所得 - 個人税 = 65 - 14 = 51
h-2 75 - 14 = 61
7)ホットドッグとハンバーガーだけを生産・消費している経済を想定しよう。その経済のある2年間のデータは次表のとおりである。

a 2010年を基準年として、名目GDP、実質GDP、GDPデフレーター、(CPI型の)固定ウエイト価格指数を、各年について計算しなさい。
b 2010年から2015年にかけて、物価はどのくらい上昇しただろうか。各財の価格と2つの価格指数、それぞれの変化率を計算しなさい。ラスパイレス指数とパーシェ指数の結果を比較しなさい。2つの指数の相違の原因を説明しなさい。
a
2010年
名目GDP:2*200 + 3*200 = 1000
実質GDP:2*200 + 3*200 = 1000
GDPデフレーター:1000 / 1000 = 1
固定ウェイト:1
2015年
名目GDP:4*250 + 4*500 = 3000
実質GDP:2*250 + 3*500 = 2000
GDPデフレーター:3000 / 2000 = 1.5
固定ウェイト:4*200 + 4*200 / 2*200 + 3*200 = 1600 / 1000 = 1.6
b
ラスパイレス:160%
パーシェ:150%
https://keisan.casio.jp/exec/system/1556264560
ラスパイレス指数は「基準時点の数量ウェイト」、パーシェ指数は「比較時点の数量ウェイト」で加重平均を行うため。
8)アビーはリンゴしか食べないものとしよう。1年目には、赤リンゴが1個1ドル、青リンゴが1個2ドルで、アビーは赤リンゴを10個購入した。2年目には、赤リンゴが1個2ドル、青リンゴが1個1ドルで、アビーは青リンゴを10個購入した。
a 各年のリンゴに関する消費者物価指数を計算しなさい。ただし、1年目を消費者のバスケットが固定される基準年とする。算出した消費者物価指数は、1年目から2年目にかけてどれだけ変化しただろうか。
b アビーがリンゴに対してそれぞれの年にいくら支出したか計算しなさい。1年目と2年目では、その額はどれだけ変化しただろうか。
c 1年目を基準年として、それぞれの年におけるアビーのリンゴへの実質支出額を計算しなさい。1年目と2年目では、その額はどれだけ変化しただろうか。
d インプリシット価格デフレーターを、名目支出額を実質支出額で割った値と定義しよう。各年のデフレーターを計算しなさい。デフレーターは1年目と2年目ではどれだけ変化しただろうか。
e アビーは、赤リンゴも青リンゴも同じくらい好きだとしよう。アビーにとって本当の生計費はどれだけ変化したことになるだろうか。その答えを、問aや問dに対する自分の答えと比較しなさい。この例は、ラスパイレス指数とパーシェ指数について、どのようなことを示しているだろうか。
a 200%
b 10ドル(1*10)/ 0ドル(2*0)|0ドル(2*0)/ 10ドル(1*10)変化なし
c 10ドル(1*10)/ 0ドル(2*0)|0ドル(1*0)/ 20ドル(2*10)10ドル
d 10 / 10 = 1|10 / 20 = 0.5 0.5
e 変化なし ラスパイレス指数は代替行動の可能性を無視しやすい、パーシェ指数は代替行動による効用水準の低下を無視しているが、効用水準の低下を伴わない代替行動も存在する。
9)経済の人口が100人で、次のような諸グループに分類されるものとしよう。25人はフルタイムの職についている。20人がパートタイムの職を1つもっていて、5人が2つのパートタイムの職を兼業している。10人が働きたくて就職活動中であり、10人が働きたいのだが就職活動をするほどの意欲はない。10人は自営業を経営している。10人が引退して、10人は小児である。
a 労働力と労働市場参加率を算出しなさい。
b 失業者数と失業率を算出しなさい。
c 総雇用者数を、家計調査の計算法と事業所調査の計算法、両方の方法で計算しなさい。

a 100 - 自営業(10) - 小児(10) - 就活拒否(10)= 70|70 / 90 = 77.8%
b 10|10 / 70(労働力人口) * 100 = 14.3%
c 25 + 20 + 5 + 10 = 60|25 + 20 + 5*2 = 55
10)1968年にロバート・ケネディ上院議員が大統領選挙に立候補したとき、彼は演説のなかでGDPについて次のように語った。
「(GDPは)われわれの子どもたちの健康や教育水準、あるいは遊びの楽しさなどを考慮していない。それは詩の美しさや夫婦の絆の強さ、公開討論の知的レベルや公務員の誠実さを含まない。それはわれわれの勇気も知恵も測らず、そして国家への忠誠心も測らない。つまり、GDPは生活を価値あるものにすること以外のすべてを測り、なぜわれわれがアメリカ人であることを誇りに思うかということ以外のアメリカに関するすべてを表すのである。」
ロバート・ケネディの言っていることは正しいのだろうか。もし正しいのであれば、なぜわれわれはGDPを重視するのか。
正しくない 生活の価値には経済厚生も当然含まれるから。
ケネディが指摘したようにGDPで測ることのできないものは存在するが、それでも経済同士を比較する指標として有効である。
11)以下の出来事が実質GDPを増やすか減らすかを考えなさい。それぞれの例において、社会の平均的な人々の経済厚生は、実質GDPと同じ方向に変化するだろうか。その理由も説明すること。
a フロリダ州をハリケーンが襲い、ディズニー・ワールドが1ヶ月間閉鎖された。
b 栽培しやすい新種の小麦が発見され、農業の収穫が増大した。
c 労働組合と経営側との対立が尖鋭化したので、ストライキが頻繁に発生した。
d 需要の減少に直面して、企業が労働者のレイオフ(一時帰休)を実施した。
e 新しい環境保護法が成立し、大量の汚染物質を排出する生産方法が禁止された。
f 学校を中退して、芝生刈りの仕事に就く高校生が増えた。
g 労働時間を減らして、子どもと過ごす時間を増やす父親が全国的に増えた。
a 減る 消費が減るから|同じ 代替行動の選択肢が減るから
b 増える 基準年価格は変わらないから|同じ 価格は下がるから効用が上がる
c1(ストライキ中に労働していないと仮定)減る その間の労働量(=生産力)が減るから(労働「力」は変わらない:一時的に休んでいるだけ)|同じ 享受できるサービスの選択肢が減るから
c2(ストライキによって賃金が上昇し再び働いたと仮定)増える 賃金が上昇するから|逆行 サービスコストが上がることが予想されるから
d 減る 供給の総量は減る|同じ 消費できるサービスが減るから。
e (その方法が経済効率的だったと仮定)減る 生産量は減る|同じ サービスコストは上昇する
f 増える 労働の総量が増えるから|同じ 労働者の数が増えればサービスコストは下がる
g 減る 生産の総量は減る|同じ サービス全般の利便性が下がることが予想される
第二部 古典派理論:長期の経済
第三章 国民所得:どこから来てどこへ行くのか
復習問題
1)経済全体の生産量を決定するのは何か。
生産要素と生産関数
生産要素:
投入物の量のこと。資本(設備や道具)・労働(時間)など。
生産関数:
投入を生産物に変換する能力(≒生産技術)のこと。多くの生産関数は「規模に関して収穫一定」(生産量が生産要素に正比例する)の特性を持つ。
2)競争的な利潤最大化企業が各生産要素の需要量をどのように決定するか説明しなさい。
競争的な利潤最大化企業は、各生産要素を追加投入した場合の収入増加と費用増加を比較することにより追加の是非を決定する(Δ利潤 = Δ収入 - Δ費用)。
追加投入時の収入増加は、販売価格 * 限界生産力によって表される。
したがって、競争的な利潤最大化企業による各生産要素の需要量は、収入(販売価格 * 各生産要素の限界生産力)と、それを調達する費用が均衡するまで(=生産要素の限界生産力が実質要素価格に等しくなるまで)となる。
労働の限界生産力と実質賃金が等しくなるまで労働は雇用され、資本の限界生産力と実質レンタル料が等しくなるまで資本はレンタルされる。
実際には均衡してしまうと利潤が出ないので均衡ギリ手前までなのでは? 生産量≠販売量なのでは? のようなツッコミも考えられるが、「利潤とは『経済学上の利潤』を指し、通常の利潤とは異なるためOK」「それはこのモデルでは考慮していない」みたいな話ですね。
労働の限界生産力:
資本量を固定した際に、労働を1単位増やした場合に得られる生産量の増分。資本の場合も同様。ほとんどの生産関数において、限界生産力は逓減する。
実質賃金:
実質賃金 = 賃金 / 価格。金額単位ではなく、生産物単位に直した賃金を表す。実質レンタル料の場合も同様。
3)所得分配において、規模に関して収穫一定の果たす役割は何か。
生産関数が規模に関して収穫一定であり、各生産要素がその限界生産力を報酬として受け取るならば、オイラーの定理より以下の式が成り立つため、生産要素に対する支払いの合計は総生産量に等しい。
F(K, L)=(MPK * K)+(MPL * L)
K:資本量、MPK:資本の限界生産力
L:労働量、MPL:労働の限界生産力
すなわち、
・規模に関して収穫一定
・利潤最大化
・競争
が満たされると、経済学上の利潤はゼロになる。
数学わからんニキなので、オイラーの定理を適用していることが正しいかどうかはよくわかりません。
4)資本が総生産量の4分の1を得ることになるコブ=ダグラス生産関数を考えなさい。
資本の所得分配率を α 、労働の所得分配率を 1-α としたとき、α = 0.25なので、題意を満たすコブ=ダグラス生産関数は
$${F(K, L)= AK^{1/4}L^{3/4}}$$
となる。
5)消費と投資を決定するのは何か。
消費は可処分所得の増加関数であり、投資は実質利子率の減少関数である。可処分所得が増えると消費は増え、実質利子率が上がると投資は減る。
可処分所得:
所得から税金を引いたもの。可処分所得が1単位増加したときの消費の変化量は、MPC(限界消費性向)で表され、消費関数の傾きはMPCとなる。
利子率:
投資資金の調達コストの尺度。調達コスト>見込み利潤であれば資金を貸した方が合理的であり、調達コスト<見込み利潤であれば投資した方が合理的。利子率は名目利子率と実質利子率(名目利子率からインフレの影響を除去したもの)に分けられ、実質利子率が真の調達コストを表す。
6)政府購入と移転支払の違いを説明しなさい。それぞれ2つずつ例をあげなさい。
政府購入は財・サービスと引き換えに支出されるが、移転支払は財・サービスを経由せず政府から個人に対して直接給付される。租税が家計の可処分所得を減らすのに対し、移転支払は家計の可処分所得を増やす。
ミサイルの購入・図書館の建設|生活保護・社会保障給付金
7)経済全体の財・サービスの生産量の需要と供給を等しくするものは何か。
利子率。利子率が高すぎれば投資は過小な状態となり、利子率が低すぎれば投資は過大な状態になる。需給が等しい状態の利子率を均衡利子率と呼ぶ。
8)政府が増税すると、消費、投資、利子率に何が生じるか説明しなさい。
Y = C + I + G の恒等式を仮定し、さらに、政府支出Gを固定する($${Y = C + I + \bar{G}}$$)。
C = C(Y - T)であり、増税によりTが上昇すると、消費Cは減少する。
恒等式から、Cの現象は投資Iの増加を意味する。
投資は実質利子率の減少関数であり、投資の増加は利子率の減少を意味する。
応用問題
1)新古典派の分配理論を用いて、以下の出来事がそれぞれ実質賃金と資本の実質レンタル料にどのような影響を与えるか予測しなさい。
a 移民が流入して、労働力が増加する。
b 地震により、資本ストックの一部が破壊される。
c 技術進歩により、生産関数が改善される。
d 高いインフレにより、すべての要素価格と総生産量が2倍になる。
a
労働力が増加すると労働の限界生産力(MPL)は低下し、労働が増えることで資本の限界生産力(MPK)の逓減が緩やかになる。
実質賃金:需要は「MPL = W / P」のため、MPLが下がると実質賃金も下がる
実質レンタル料:需要は「MPK = R / P」のため、実質レンタル料は上がる
b
資本ストックの減少によりMPKは上昇し、MPLは下がる。
実質賃金:下がる
実質レンタル料:上がる
c
生産量Yについて「Y = F(K, L)」であり、分配の際は「Y =(MPK * K)+(MPL * L)」であるから、生産関数の改善により生産量は上昇し、したがってMPK * KもMPL * Lも上昇するはず。KもLも変化していない場合、
実質賃金:上がる
実質レンタル料:上がる
d
要素価格が2倍になるので、今まで「W / P」で定義されていた実質賃金は「2W / P」となる。仮にP(インフレ後の販売価格)が一定のままなら、
実質賃金:上がる
実質レンタル料:上がる
ただ、題意的には「実質賃金も実質レンタル料も変わらない」が正解っぽい空気は感じるので、私が何かわかってない可能性は感じます。(たぶん2W / 2P = W / P って話をさせたいんだと思いますw)
2)中世のヨーロッパの生産関数が$${Y = K^{0.5}L^{0.5}}$$であるとしよう。ただし、Kは土地の広さ、Lは労働量である。初期の土地の広さが100単位、労働量が100単位の経済である。電卓と本章の方程式を用いて、以下の問いについて数値で答えなさい。
a 経済全体で生産量は何単位となるか。
b 賃金と地代はいくらになるか。
c 労働者が受け取る生産物の割合はどれだけになるか。
d もし伝染病で人口の半分が失われたならば、生産量はどれだけになるか。
e そのとき、賃金と地代はいくらになるか。
a $${Y = 100^{0.5}100^{0.5} = 10 * 10 = 100}$$
b 50|50
c 50%
d $${Y = 50^{0.5}100^{0.5} = 70.71}$$
e 35.36(d*c)|35.36(d*(1-c))
3)資本と労働がどもに10%ずつ増加しても、生産量が10%未満しか増加しない生産関数のことを、「規模に関して収穫逓減」という。また、生産量が10%より多く増加する生産関数は「規模に関して収穫逓増」であるという。生産関数はなぜ規模に関して収穫逓減や収穫逓増になるのだろうか。
各生産要素の限界生産力が変動するから。
規模に関して収穫逓減:
農地を増やした際に、一方が他方よりも日当たりが悪いケース
規模に関して収穫逓増:
労働を増やした際に、得意不得意の作業を分担して作業効率が上がるケース
4)コブ=ダグラス型の生産関数において α = 0.3 とする。
a 所得のなかから資本と労働が受け取る割合はそれぞれどれだけか。
b 移民により労働力が10%増加したとしよう。総生産量には何が起こるか(パーセントで答えなさい)。また、資本のレンタル料と実質賃金には何が起こるか。
c 海外から資本が贈与されて資本ストックが10%増加したとしよう。総生産量には何が起こるか(パーセントで答えなさい)。資本のレンタル料と実質賃金には何が起こるか。
d 技術進歩によりパラメーターAの値が10%上昇したとしよう。総生産量には何が起こるか(パーセントで答えなさい)。資本のレンタル料と実質賃金には何が起こるか。
α = 0.3なので、$${F(K, L)= AK^{0.3}L^{0.7}}$$(①)
a
資本3割|労働7割
b
総生産量は、$${\frac{AK^{0.3}(1.1L)^{0.7}}{AK^{0.3}L^{0.7}} ≒ 1.069}$$より6.9%上昇する。
資本の限界生産力は$${MPK = αAK^{α-1}L^{1-α}}$$によって表され、労働の限界生産力は$${MPL = (1 - α)AK^{α}L^{-α}}$$によって表される。
したがって、資本のレンタル料は、$${\frac{0.3AK^{-0.7}(1.1L)^{0.7}}{0.3AK^{-0.7}L^{0.7}} ≒ 1.069}$$より6.9%上昇し、
実質賃金は、$${\frac{0.7AK^{0.3}(1.1L)^{-0.3}}{0.7AK^{0.3}L^{-0.3}} ≒ 0.972}$$より2.8%下降する。
c
総生産量は、$${\frac{A(1.1K)^{0.3}L^{0.7}}{AK^{0.3}L^{0.7}} ≒ 1.029}$$より2.9%上昇する。
資本のレンタル料は、$${\frac{0.3A(1.1K)^{-0.7}L^{0.7}}{0.3AK^{-0.7}L^{0.7}} ≒ 0.935}$$より6.5%下降し、
実質賃金は、$${\frac{0.7A(1.1K)^{0.3}L^{-0.3}}{0.7AK^{0.3}L^{-0.3}} ≒ 1.029}$$より2.9%上昇する。
d
①より、総生産量は10%上昇する。資本のレンタル料も実質賃金も10%上昇する(総生産量が10%上昇し、要素分配率は変化しないため)。
5)図3-5が示すように、アメリカのデータでは、総所得に占める労働の分配率はほぼ一定である。また、表3-1が示すように、実質賃金の趨勢は、労働生産力の趨勢と一致している。これらの事実はどのように関連しているだろうか。もし2番目の事実が間違っていた場合、1番目の事実は正しいといえるだろうか。労働分配率を数学的に表現して答えなさい。


『マンキュー マクロ経済学I 入門篇(第4版)』
コブ=ダグラス型の生産関数$${F(K, L)= AK^{α}L^{1-α}}$$が成り立つと仮定する。題意(1番目の事実)より、$${F(K, L)= AK^{\bar{α}}L^{1-\bar{α}}}$$。したがって、$${労働分配率 = (1 - \bar{α})}$$である。
実質賃金 = $${\frac{W}{P}}$$と表記できる。これは限界生産力に等しいため、$${\frac{W}{P} = \frac{(1 - \bar{α})Y}{L}}$$となり、労働への総支払額はMPL * Lなので、$${(1 - \bar{α})Y}$$である(①)。
ここで、成長前の総生産をY・成長後をY'とすると、表3-1における「労働生産性の成長」は、$${\frac{Y'}{Y}}$$、「実質賃金の成長」は、①より、$${\frac{(1 - \bar{α})Y'}{(1 - \bar{α})Y * インプリシット価格デフレーター} = \frac{Y'}{Y * インプリシット価格デフレーター}}$$と表せる。
したがって、このモデルにおいて「実質賃金の成長」と「労働生産性の成長」に差異をもたらす概念は価格デフレーターであり、2番目の事実が正しいならば、インフレが発生していないことを意味し、2番目の事実が誤っていた場合、かつインフレが発生していない場合であれば、1番目の事実(分配率が一定であるという仮定)が誤っていることを意味する。
6)新古典派の分配理論によれば、労働者が受け取る実質賃金は、その人の生産性次第である。この洞察を用いて、農民と理容師という2つの労働者グループの所得について検討してみよう。WfとWbをそれぞれ農民と理容師の名目賃金とし、PfとPbを農産物の価格と散髪の料金、そしてAfとAbを農民と理容師の限界生産性だとしよう。
a 上で定義した6つの変数について、どのような単位で計算されるかをできるだけ正確に述べなさい(ヒント:答えはそれぞれYの単位で計ってX単位となるという形になる)。
b 過去1世紀に、農民の生産性Afは技術進歩により著しく上昇した。新古典派理論によると、農民の実質賃金Wf/Pfに何が起こったはずか。
c 同じ期間に理容師の生産性Abはほとんど変わらなかった。理容師の実質賃金Wb/Pbに何が起こったはずか。この実質賃金はどのような単位で計算されるか。
d 長期において労働者が農民と理容師の間を自由に転職できるとしよう。この流動性は農民と理容師の名目賃金WfとWbにとって何を意味するか。
e 問dの答えは、散髪の食糧に対する相対価格Pb/Pfについて何を意味するか。
f 理容師と農民が同量の財・サービスの組み合わせを消費するとしよう。農業の技術進歩からより大きな便益を得るのは農民と理容師のどちらだろうか。その答えがどのように問bと問cの実質賃金の答えと矛盾しないかについて説明しなさい。
a
名目賃金:
労働に対し、「時間単位で支払われた」「通貨単位の報酬」
価格・料金:
「生産単位当たりの」「通貨単位の金額」
限界生産性(限界生産力と同じ概念だと解釈):
「労働単位当たりの」「生産量単位」
b
限界生産力が上がると実質賃金も上がる。
c
限界生産力が変わらなければ、実質賃金も変わらない。
実質賃金は、労働への「生産物単位で測った」「通貨単位の報酬」として計算される。理容師の場合、Wb / Pb = ヘアカット時間あたりの報酬 / ヘアカット価格。
d
Wf = Wb になる。
e
限界生産性について$${Af = \frac{Wf}{Pf}}$$、$${Ab = \frac{Wb}{Pb}}$$と表せるので、$${Pf = \frac{Wf}{Af}、Pb = \frac{Wb}{Ab}}$$。したがって、$${\frac{Pb}{Pf} = \frac{\frac{Wb}{Ab}}{\frac{Wf}{Af}}}$$(①)である。
Wf = Wb を前提とすると、①は$${\frac{Af}{Ab}}$$と整理できるため、与えられた相対価格は各生産要素の限界生産性によって決定されることがわかる。
f
転職の流動性が担保されている前提においては、農業の技術進歩から得られる便益は農民においても理容師においても等しい。
問b、cでは、農民の実質賃金が上がり、理容師の実質賃金が変わらないことを示したが、実質賃金の差異は名目賃金の差異を意味しない。名目賃金が等しければ、同量の財・サービスから得られる便益は等しくなる。
7)(代数の知識が必要な問題)3種類の投入要素があるコブ=ダグラス生産関数を考えよう。資本(機械の台数)をK、労働(労働者数)をL、人的資本(労働者のなかで大学卒の人数)をHとする。生産関数は、
$${Y = K^{1/3}L^{1/3}H^{1/3}}$$
である。
a 労働の限界生産力を表す式を求めなさい。人的資本の量が増えると、労働の限界生産力にどのような影響を与えるだろうか。
b 人的資本の限界生産力を表す式を求めなさい。人的資本の量が増えると、人的資本の限界生産力にどのような影響を与えるだろうか。
c 労働に支払われる所得の割合はどれだけか。人的資本に支払われる所得の割合はどれだけか。この経済の国民所得勘定では、労働者は総所得のうちどれだけの割合を受け取っているように表されるか(ヒント:人的資本の報酬がどこに計上されるかを考えなさい)。
d 未熟練労働者は労働の限界生産物を受け取り、熟練労働者は労働の限界生産力に加えて人的資本の限界生産力も受け取るとする。問aと問bへの解答を用いて、熟練賃金の未熟練賃金に対する比率を求めなさい。人的資本の量が増えると、この比率にどのような影響を与えるかを説明しなさい。
e 大学への奨学金に政府が財政的補助をすることは、より平等な社会をつくる方策であると提唱する人々がいる。一方で、奨学金は大学に行く人だけを助けると主張する人々もいる。これまでの問いに対する解答から、この論争に何がいえるだろうか。
a
$${MPL = \frac{1}{3}K^{1/3}H^{1/3}L^{-2/3}}$$
上式のHが増えればMPLも増える。
b
$${MPH = \frac{1}{3}K^{1/3}L^{1/3}H^{-2/3}}$$
上式のHが増えるとMPHは減る。
c
労働:$${\frac{1}{3}}$$
人的資本:$${\frac{1}{3}}$$
労働者:$${\frac{2}{3}}$$(労働+人的資本)
d
問a,bより、
$${\frac{熟練}{未熟練} = \frac{MPL + MPH}{MPL} = \frac{\frac{1}{3}K^{1/3}H^{1/3}L^{-2/3} + \frac{1}{3}K^{1/3}L^{1/3}H^{-2/3}}{\frac{1}{3}K^{1/3}H^{1/3}L^{-2/3}} = 1 + \frac{L}{H}}$$
Hが増えると分母が減るため、この比率は減る。
e
奨学金により大学に行くことができる人が増えると、Hが増える。問dより、Hが増えると人的資本の賃金への寄与度が下がり、より平等な社会をつくる方策になる(大学に行かない人にとっても、全体で見ると賃金格差の面でメリットがある)。
8)政府が1000億ドル増税したとしよう。限界消費性向が0.6のとき、以下のものにはどれだけの額の増減があるか。
a 公的貯蓄
b 民間貯蓄
c 国民貯蓄
d 投資
各項は以下のように表せる。
国民貯蓄 = Y - C - G = 民間貯蓄 + 公的貯蓄
民間貯蓄 = Y - T - C
公的貯蓄 = T - G
投資 = 国民貯蓄
a
Tが1000億ドル増えると、公的貯蓄も1000億ドル増える。
b
限界消費性向が0.6なので、消費Cは600億ドル減る(C = C(Y - T))。
-1000億ドル -(-600億ドル)= -400億ドルなので、400億ドル減る。
c
a + b = 600億ドル増える。
d
600億ドル増える。
9)消費者に自信が出て将来所得が上がると予想するようになり、いま消費したい量が大きくなるとしよう。これは消費関数の上方シフトと解釈できる。この消費関数のシフトは投資と利子率にどのような影響を与えるか。
消費関数の上方シフトは、限界消費性向の上昇を意味する。消費が増えると、貯蓄が減り、それによって投資も減り、利子率は上昇する。
10)以下の諸式で表される経済を考えよう。
Y = C + I + G
Y = 8000
G = 2500
T = 2000
C = 1000 + 2/3(Y - T)
I = 1200 - 100r
a この経済における民間貯蓄、公的貯蓄、国民貯蓄を計算しなさい。
b 均衡利子率を求めなさい。
c Gが500に減少するときの民間貯蓄、公的貯蓄、国民貯蓄を計算しなさい。
d 新しい均衡利子率を求めなさい。
国民貯蓄 = Y - C - G = 民間貯蓄 + 公的貯蓄
民間貯蓄 = Y - T - C
公的貯蓄 = T - G
a
民間貯蓄:
Y - T - C = 8000 - 2000 -(1000 + 2/3(8000 - 2000))= 1000
公的貯蓄:
T - G = 2000 - 2500 = -500
国民貯蓄:
1000 +(-500)= 500
b
Y = C + I + G より、I = Y - C - G なので、
1200-100r = 8000 - 5000 - 2500
100r = 700
r = 7%
c
民間貯蓄:
Y - T - C = 8000 - 2000 -(1000 + 2/3(8000 - 2000))= 1000
公的貯蓄:
T - G = 2000 - 500 = 1500
国民貯蓄:
1000 + 1500 = 2500
d
1200 - 100r = 8000 - 5000 - 500
100r = -1300
r = -13%(そんなことある??)
11)政府が増税するとともに、政府購入を同額だけ増加させたとする。財政収支を変化させないこの税制の変更によって、利子率と投資に何が起こるか。その答えは限界消費性向の大きさに依存するか説明しなさい。
国民貯蓄 = Y - C - G = 民間貯蓄 + 公的貯蓄
民間貯蓄 = Y - T - C
公的貯蓄 = T - G
投資 = 国民貯蓄
増加した税額(政府購入)をαとすると、増加後は以下となる。
民間貯蓄 = Y - (T + α) - C
公的貯蓄 = (T + α) - (G + α)
したがって、公的貯蓄には変化がなく、民間貯蓄は減少する(両者の合計である国民貯蓄も減少する)。
国民貯蓄の減少により投資は減少し、利子率は上昇する。
C = C(Y - (T + α))の関数が適用できるため、民間貯蓄の減少幅は限界消費性向の大きさに左右される(限界消費性向が大きいほど民間貯蓄の減少幅は大きくなり、限界消費性向が小さいほど民間貯蓄の現象幅は小さくなる)
12)政府が投資税額控除などによって投資に補助をする際、特定の投資にのみ補助をすることがある。この問題では、そうしたケースの影響を考えよう。経済には設備投資と住宅投資という、2つのタイプの投資があるとしよう。利子率は国民貯蓄と総投資、すなわち設備投資と住宅投資の合計と均衡するように調整されるとしよう。ここで、政府は設備投資にのみ投資税額控除を設けたとする。
a この政策は、設備投資の需要曲線と住宅投資の需要曲線にそれぞれどのような影響を与えるか。
b 貸付資金の需要曲線と供給曲線を描きなさい。この政策は貸付資金の需要と供給にどのような影響を与えるか。均衡利子率には何が生じるか。
c 元の均衡と新しい均衡を比較しなさい。この政策は総投資量にどのような影響を与えるか。また、設備投資量と住宅投資量についてはどうか。
a
設備投資は右方シフトする。住宅投資は変化しない。
b
本問題の仮定では、「利子率は国民貯蓄と総投資、すなわち設備投資と住宅投資の合計と均衡するように調整」されている。したがって、そのままこの図。消費や貯蓄が利子率に依存する仮定の元では、この図式は成立しない。
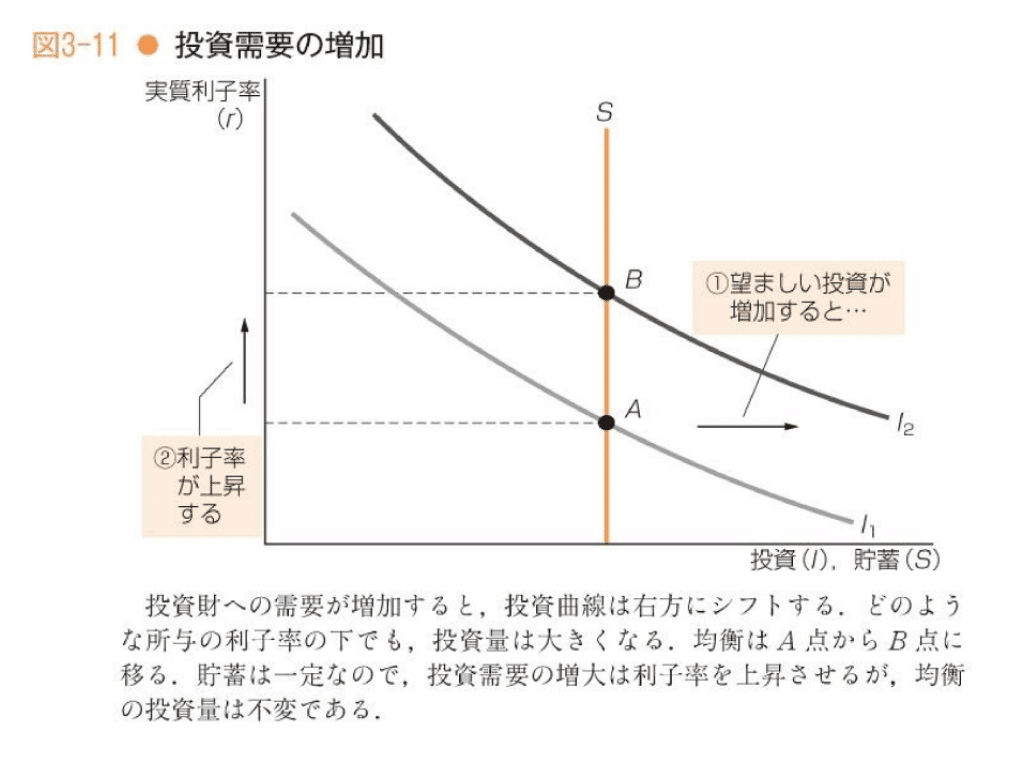
c
意外な結論だが、bより、総投資量は税金の影響を受けない。投資量が固定されている世界線では、設備投資量が増え、その分、住宅投資量が減る。
13)消費が利子率の関数であるとしよう。これにより、政府購入の増加が投資、消費、国民貯蓄、利子率にもたらす影響について、本章の結論にどのような影響を与えるか。
投資と国民貯蓄に対する影響は、同じものとして扱うこととする。(①)
本章では、政府購入がΔG増えるときの経済への影響について、「政府購入の増加は利子率を上昇させて投資(国民貯蓄)を減少させる」としていた。
この際に消費が利子率の関数であるとすれば、
消費:
利子率の上昇につれて徐々に貯蓄のインセンティブが高くなり、減退するようになる。
投資(①より国民貯蓄):
利子率が上昇するにつれて消費が貯蓄に回るようになり、減少幅は徐々に緩やかになる。
利子率:
消費が貯蓄に回り始めるにつれて、利子率の上昇は緩やかになる。
14)マクロ経済のデータでは、投資と利子率の間に強い相関がみられない。なぜそうなのかについて検討しよう。(右上がりの)貸付資金の供給と(右上がりの)貸付資金の需要を均衡させるように利子率が調整されるモデルを用いなさい。
a 貸付資金への需要は安定的だが、供給が毎年変動したとしよう。この供給の変動は、何を引き起こしたか。この場合、投資と利子率の間にどのような相関が見出せるか。
b 貸付資金への供給は安定的だが、需要が毎年変動したとしよう。この需要の変動は、何を引き起こしたか。この場合、投資と利子率の間にどのような相関が見出せるか。
c 需要と供給がともに変動したとしよう。投資と利子率の散布図を作成すると、何が見出せるか。
d 上の3つの場合のうち、あなたの経験からみて最も現実性が高いのはどれか。またそれはなぜか。
a

↑のような図になることが想定される。投資と利子率は負の相関になる。
b
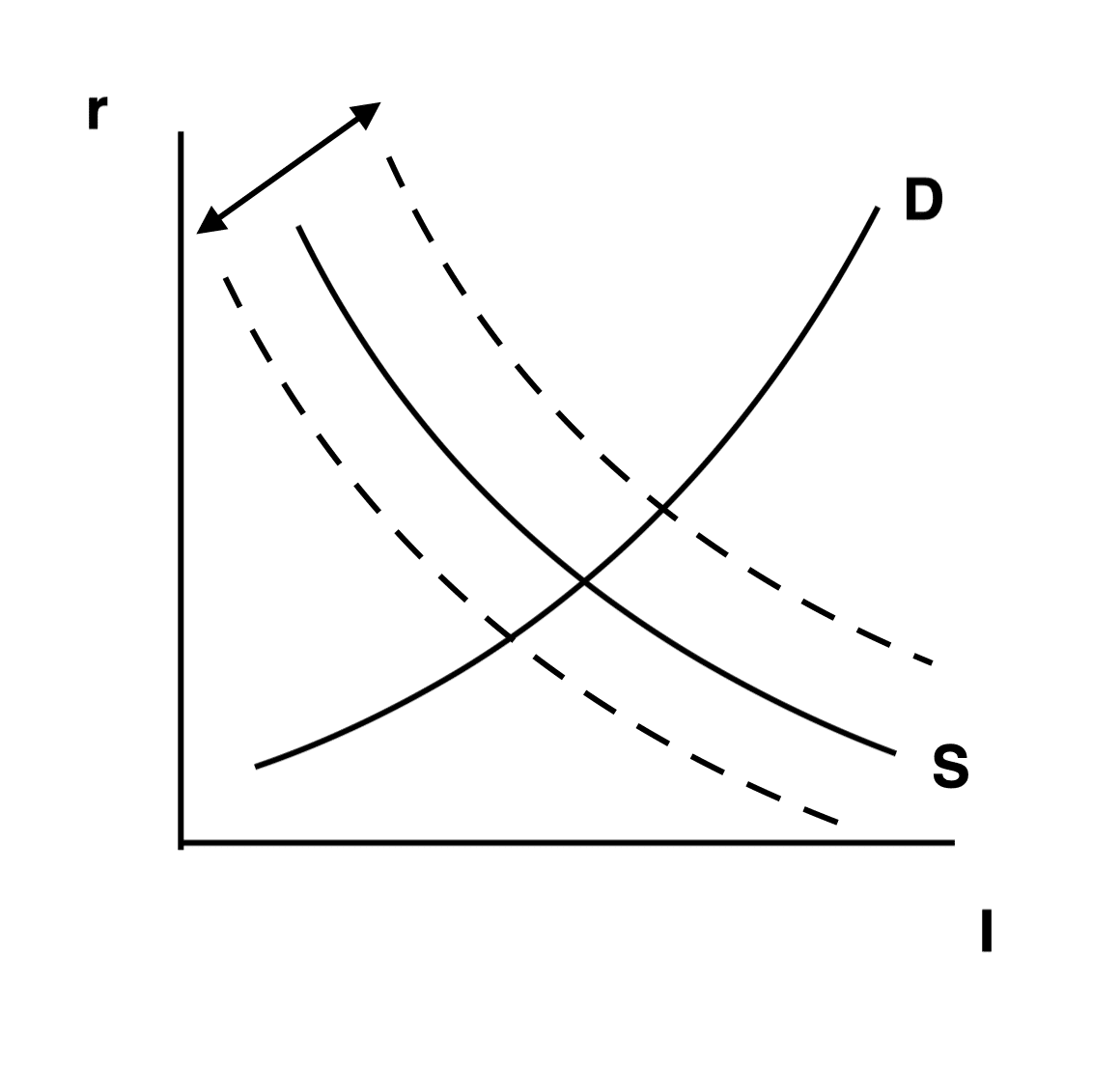
↑のような図になることが想定される。投資と利子率は正の相関になる。
c

投資と利子率は正の相関にも負の相関にもなりうる。
d
cが最も現実性が高いと思われる。Uniswapでの流動性供給の経験上、現実世界における需給はそれぞれ変動している気がする。
第四章 貨幣システム:どのようなものでどのように機能するか
復習問題
1)貨幣の機能を列挙しなさい。
価値貯蔵手段:
購買力を現在から将来へと移転する。
計算単位:
価格づけの単位や負債を記録する単位として機能する。
交換手段:
財・サービスを購入する手段となる。
2)不換紙幣とは何か。商品貨幣とは何か。
不換紙幣:
内在的な価値を持たない貨幣のこと。政府の宣言・命令(fiat)によって地位を獲得している。
商品貨幣:
内在的な価値を持つ商品が貨幣として用いられているもの。金、あるいは金と兌換可能な紙幣が代表例。
3)公開市場操作とは何か。また、それはどのようにしてマネーサプライに影響を与えるのか。
中央銀行による国債の売買のこと。
中央銀行が民間から国債を買うと、支払った金額がマネタリーベースの増加となり、マネーサプライの増大に繋がる。中央銀行が民間に国債を売却すると、受け取った金額がマネタリーベースの減少となり、マネーサプライの減少をもたらす。
4)どのようにして銀行が貨幣(信用)を創造するのかを説明しなさい。
銀行の信用創造機能は、部分準備制度を前提として成り立つ。
「準備」とは、「銀行が受け入れているが貸し出さない預金」を指す。
部分準備制度の下では、銀行は定められた準備・預金比率を満たす準備を残し、預金の貸出を行う。
貸出が行われると、
・預金者は預金した金額分の要求払い預金を保有し
・借入者は借り入れた分の現金通貨を保有する
ため、貸出分の貨幣が生み出される(信用創造が行われる)。
借入者が借り入れた現金を預金した場合、その預金にも同様の操作が行われる。この過程が繰り返されることで、マネーサプライが増大する。
上記の前提において、マネーサプライの総量は無限等比数列の和として計算できるため、1/rrで表せる(rr = 準備・預金比率)。
例えば最初に預けられた金額が1000ドルで、準備・預金比率が20%(0.2)の場合、マネーサプライの総量は5000ドルとなる。
5)中央銀行がマネーサプライをコントロールするためのさまざまな政策手段とは何か。
①マネタリーベースを変化させる
→ 公開市場操作(復習問題3で書いたので省略)、銀行への準備の貸出(公定歩合の変更など)
中央銀行は、他から資金を入手することが困難な銀行に貸出をするとき、「最後の貸し手」として行動する。
公定歩合:
中央銀行が貸付を行う際の利子率。例えば、公定歩合が下がると、準備の借入費用が下がり、より多くの民間銀行が中央銀行貸出を利用するようになる。その結果、マネタリーベースは増え、マネーサプライは増大する。
②貨幣乗数を変化させる
→ 必要準備の変更、準備預金付利
貨幣乗数は(cr + 1) / (cr + rr)。crは現金・預金比率、rrは準備・預金比率。
したがって上記は、貨幣乗数のうち分母の部分をいじる操作となる。
必要準備:
必要準備は、中央銀行が民間銀行に対し、保有すべき最低準備・預金比率を課している規制のこと。仮に必要準備を引き上げると、rrの上昇をもたらし、マネーサプライの減少につながる。
準備預金付利:
銀行が中央銀行に預け金として準備を保有する際に、その準備金に対して利子を支払うこと。この利率が上がると、民間銀行は準備を増やし(rrが上がる)、貨幣乗数を小さくする。その結果マネーサプライは減る。
6)銀行危機がマネーサプライの減少を生じさせる可能性があるのはなぜだろうか。
大規模な銀行破綻は、民間銀行と預金者双方の行動を変化させ、マネーサプライを減少させる可能性があるから。
銀行破綻が銀行システムに対する預金者の信任を低下させると、現金・預金比率が上昇する。預金が引き出されると、準備が減少し、銀行はそれに対応して貸出の縮小・回収を進める。その結果、信用創造の過程が逆方向に進み、マネーサプライは減少する。
銀行破綻が銀行家をより慎重にさせると、準備・預金比率が上昇する。銀行が取付を恐れ、必要準備以上の準備を保有するようになると、マネーサプライは減少する。
応用問題
1)貨幣の機能を3つあげなさい。下記のものはどの機能を果たし、どれを果たしていないだろうか。
・クレジット・カード
・レンブラントの絵
・地下鉄乗車券専用の硬貨(トークン)
価値貯蔵手段・計算単位・交換手段
クレジットカード
△△○
レンブラントの絵
○××
地下鉄乗車専用の硬貨(トークン)
△△△
SuicaとかPasmoとか、現代ではほぼ○寄りの△な気がする
2)次の出来事がどのようにして、マネタリーベース、貨幣乗数、マネーサプライに影響を与えるかについて説明しなさい。
a 連邦準備が公開市場操作で債権を購入する。
b 連邦準備が、銀行の保有する準備に支払う利子率を引き上げる。
c 連邦準備が期日物入札型貸出(TAF)を通じて銀行に貸出を行う。
d ATMにコンピューターウィルスの攻撃があったといううわさが広まって、人々が要求払い預金でなく現金通貨で保有する貨幣の量を増やす。
e 連邦準備がニューヨークの5番街の上にヘリコプターを飛ばし、100ドル紙幣をばらまく。
C:現金通貨
D:要求払い預金
R:銀行準備
M:マネーサプライ
B:マネタリーベース
cr:現金・預金比率
rr:準備・預金比率
M = C + D(①)
B = C + R(②)
M = 貨幣乗数 * B(③)
貨幣乗数:$${\frac{cr + 1}{cr + rr}}$$(④)
a
マネタリーベース、マネーサプライ
復習問題3で書いたので略。
貨幣乗数
操作がcrとrrに影響を与えない限り影響はない。
b
貨幣乗数、マネーサプライ
復習問題5の②で書いたため略(準備預金付利)。
マネタリーベース
変化しない(Cが減ってRが増える)
c
マネタリーベース、マネーサプライ
貸出量が増えるとBも増え、それによりMも増える。
貨幣乗数
操作がcrとrrに影響を与えない限り影響はない。
d
この現象は社会環境の変化ではなく一時的なシステム不信であるため、持続しないものとする。
マネタリーベース
②においてCは増えRは減るが、この増減は上記の仮定よりrrの変化を伴わないため、同値である。したがってBは変化しない。
貨幣乗数
④におけるcrが増えrrは変わらない。crが増えると貨幣乗数は小さくなる。
マネーサプライ
③より、貨幣乗数が小さくなればMも減少する。
e
マネタリーベース、マネーサプライ
紙幣が増えるため増える。
貨幣乗数
紙幣を拾った人の行動次第。現金として保有すればcrが上がり貨幣乗数は小さくなる。預金として預け入れれば貨幣乗数は大きくなる。
3)ある経済のマネタリーベースとして1000枚の1ドル札がある。以下の問a〜dの場合のマネーサプライを計算し、その後、問eに答えなさい。
a すべての貨幣が現金通貨として保有される。
b すべての貨幣が要求払い預金として保有される。銀行が預金の100%を準備として保有する。
c すべての貨幣が要求払い預金として保有される。銀行は預金の20%を準備として保有する。
d 人々は現金通貨と要求払い預金を同額保有する。銀行は預金の20%を準備として保有する。
e 中央銀行はマネーサプライを10%増加させると決定する。上の4つの場合において、それぞれマネタリーベースをどれだけ増やさなければならないか。
C:現金通貨
D:要求払い預金
R:銀行準備
M:マネーサプライ
B:マネタリーベース
cr:現金・預金比率
rr:準備・預金比率
M = C + D(①)
B = C + R(②)
M = 貨幣乗数 * B(③)
貨幣乗数:$${\frac{cr + 1}{cr + rr}}$$(④)
a
M = 1000 + 0 = 1000
b
信用創造がない世界線なので、M = 1000
c
1000 * $${\frac{1}{rr}}$$ = 1000 * $${\frac{1}{0.2}}$$ = 5000
d
貨幣乗数 = $${\frac{cr + 1}{cr + rr}}$$ = $${\frac{1 + 1}{1 + 0.2}}$$ ≒ 1.667
③より、M = 1667
e
③より、いずれの場合においても10%
4)ウィキナム国では人々は1000ドルの現金通貨と、唯一の銀行であるウィキ銀行に4000ドルの要求払い預金を保有する。準備・預金比率は0.25である。
a マネーサプライ、マネタリーベース、貨幣乗数はいくらか。
b ウィキ銀行は預金を受け入れ、貸付を行い、資本は持たないという、単純な銀行であるとする。ウィキ銀行の貸借対照表を示しなさい。銀行が保有する貸付残高の大きさはいくらか。
c ウィキナム国の中央銀行はマネーサプライを10%増やしたい。中央銀行は公開市場操作で国債を購入すべきか、売却すべきか。貨幣乗数が変わらないと仮定して、中央銀行は何ドルの取引をする必要があるか計算しなさい。
C:現金通貨
D:要求払い預金
R:銀行準備
M:マネーサプライ
B:マネタリーベース
cr:現金・預金比率
rr:準備・預金比率
M = C + D(①)
B = C + R(②)
M = 貨幣乗数 * B(③)
貨幣乗数:$${\frac{cr + 1}{cr + rr}}$$(④)
C = 1000
D = 4000
rr = 0.25
R = D * rr = 1000
cr = C / D = 0.25
a
M = C + D = 1000 + 4000 = 5000
B = C + R = 2000
貨幣乗数 = $${\frac{cr + 1}{cr + rr}}$$ = $${\frac{0.25 + 1}{0.25 + 0.25}}$$ = 2.5
b

c
マネーサプライを増やしたいのであれば、中央銀行は国債を購入すべき。
国債購入に使われた金額はCの増加となる。
M = 2.5Bの関係においてMを10%増やしたいため、
ΔM = 5000*0.1 = 500 = 2.5ΔB となればよいから、ΔB = 200。
(国は預金しないものとする)
ΔB = ΔC = 200
5)ペニカ国の経済では、マネタリーベースが1000ドルである。人々は貨幣の3分の1を現金通貨で保有する。(そして3分の2を銀行預金で保有する。)銀行は預金の3分の1を準備として保有する。
a 準備・預金比率、現金・預金比率、貨幣乗数、マネーサプライはそれぞれいくらか。
b ある日、人々は銀行システムへの懸念を持ち、貨幣の半分を現金通貨で保有したいと思うようになった。もし中央銀行が何もしなければ、マネーサプライはいくらになるか。
c もし中央銀行が、このパニックに直面して、マネーサプライを元の水準に維持するために公開市場操作を行いたいと考えるならば、国債を購入するか、あるいは売却するか。中央銀行は何ドルの取引をする必要があるか計算しなさい。
C:現金通貨
D:要求払い預金
R:銀行準備
M:マネーサプライ
B:マネタリーベース
cr:現金・預金比率
rr:準備・預金比率
M = C + D(①)
B = C + R(②)
M = 貨幣乗数 * B(③)
貨幣乗数:$${\frac{cr + 1}{cr + rr}}$$(④)
B = 1000
a
rr = $${\frac{1}{3}}$$
cr = $${\frac{\frac{1}{3}}{\frac{2}{3}}}$$ = $${\frac{1}{2}}$$
貨幣乗数 = $${\frac{cr + 1}{cr + rr}}$$ = $${\frac{\frac{1}{2} + 1}{\frac{1}{2} + \frac{1}{3}}}$$ = 1.8
M = 1.8 * 1000 = 1800
b
これはcrが1に変化したということなので、
貨幣乗数 = $${\frac{cr + 1}{cr + rr}}$$ = $${\frac{1 + 1}{1 + 1/3}}$$ = 1.5
M = 1.5 * 1000 = 1500
c
国は預金しないものとする。
ΔM = 1800 - 1500 = 300 = 1.5B
B = 200 なので、
国債を200買う必要がある。
6)この章のケース・スタディで議論したように、1929年から33年にかけて、現金・預金比率と準備・預金比率が上昇したことにより、マネーサプライは減少した。マネーサプライのモデルと表4-2のデータを用いて、このエピソードに関する以下の仮想的問題に答えなさい。

a 現金・預金比率は事実通りに上昇したが、準備・預金比率が変わらなかったとしたら、マネーサプライはどうなっていただろうか。
b 準備・預金比率は事実通りに上昇したが、現金・預金比率が変わらなかったとしたら、マネーサプライはどうなっていただろうか。
c マネーサプライの減少に対して責任が大きいのは、2つの比率のうちのどちらの上昇だろうか。
C:現金通貨
D:要求払い預金
R:銀行準備
M:マネーサプライ
B:マネタリーベース
cr:現金・預金比率
rr:準備・預金比率
M = C + D(①)
B = C + R(②)
M = 貨幣乗数 * B(③)
貨幣乗数:$${\frac{cr + 1}{cr + rr}}$$(④)
a
M = $${\frac{cr + 1}{cr + rr}}$$B = $${\frac{0.41 + 1}{0.41 + 0.14}}$$ * 8.4 ≒ 21.53
b
M = $${\frac{cr + 1}{cr + rr}}$$B = $${\frac{0.17 + 1}{0.17 + 0.21}}$$ * 8.4 ≒ 25.86
c
今回の結果においては現金・預金比率。
7)税収を増やすため、1932年に連邦政府は、銀行口座の預金をもとに書かれる小切手に2セントの課税をした(今日のドルで表すと、この税は小切手1枚当たり約34セントに相当するであろう)。
a 小切手への課税が現金・預金比率にどのような影響を与えたかを説明しなさい。
b 部分準備制度の下でのマネーサプライのモデルを用いて、この課税がマネーサプライにどのような影響を与えたかを議論しなさい。
c 多くの経済学者は、1930年代の大恐慌の深刻さは、一つにはマネーサプライの減少が原因であると考える。こうした視点からは、小切手への課税は、大恐慌の最中に実施すべき政策として適切だっただろうか。
a
現金決済需要が上がるため、crは上昇する。
b
crが上昇すると、貨幣乗数が小さくなるため、Mも小さくなる。
c
銀行への信任が落ちるような状況において、更に現金・預金比率を引き下げることが予想される政策を打つのは適切ではない。
8)レバレッジ率が20となる銀行の貸借対照表の例を挙げなさい。もし銀行の資産の価値が2%上昇したら、この銀行のオーナーのエクイティの価値はどうなるか。また、銀行の資産価値がどれほど低下すると、この銀行の資本はゼロにまで減少するか。

この例で言うと、銀行の資産価値が2%上昇すると、オーナーのエクイティは1000 * 0.02 = 20ドル上昇する。
レバレッジ率が20なので、銀行の資産価値が5%下降すると資本が0になる。
9)ジミー・ポール・ミラーは自分自身のJPM銀行を開設する。オーナーとして、ジミーは自己資金を2000ドル投じる。そしてJPMはジミーの叔父から4000ドルを長期借入れし、近所の人たちから要求払い預金で1万4000ドルを受け入れ、米国財務相証券を7000ドル購入し、地域の事業者の新規投資の資金として1万ドルを融資し、銀行の資産の残りを連邦準備で準備として保有する。
a JPMの貸借対照表を示しなさい。JPMのレバレッジ率はいくらか。
b 景気後退により、地域の事業者の5%が破産して、貸付が債務不履行になる。JPMの新しい貸借対照表を示しなさい。JPMの資産価値の何%が低下するか。JPMの資本は何%低下するか。
a

レバレッジ率 = (3000 + 10000 + 7000) / 2000 = 10
b

低下した資産価値は、500 / 20000 = 2.5%
資本は500 / 2000 = 25%
これはレバレッジ率どおりの結果である。
第五章 インフレーション:原因と影響と社会的コスト
復習問題
1)数量方程式を書き、説明しなさい。
M * V = P * T
M:貨幣量。
V:貨幣の取引流通速度。一定期間内に貨幣が何回所有者を替えたか。
P:取引金額。
T:一定期間内の財・サービスと貨幣との取引回数の総数。
2)貨幣の流通速度一定という仮定が何を意味するかを説明しなさい。
$${MV = PY}$$という数量方程式を想定した際に、Vが一定と仮定できるならば($${M\bar{V} = PY}$$)、経済の総生産額は貨幣量によって決まるということが言える(貨幣数量説)。
3)インフレ税を支払うのは誰か。
貨幣の所有者。物価が上昇すると、財布の中にある現金の実質価値が減少する。政府が資金調達のために新しい紙幣を印刷すると、公衆が元から保有している紙幣の価値が低下する。
4)インフレ率が6%から8%へと上昇したとき、フィッシャー効果によれば、実質利子率と名目利子率はどう変化するだろうか。
フィッシャー方程式:
名目利子率をi、実質利子率をr、インフレ率をπとしたとき、
i = r + π
フィッシャー効果:
インフレ率(π)と名目利子率(i)が1対1対応にあること。
フィッシャー効果によれば、インフレ率が2%上昇すると名目利子率が2%上昇する。実質利子率には影響を与えない。
5)インフレーションのコストを思い当たるだけ列挙し、あなた自身の評価にしたがって各コストの重要性をランクづけしなさい。
<予想されたインフレーションコスト>
靴底コスト:
インフレ税による貨幣保有の歪み(貨幣保有を減少させることによる不便さ)。インフレ率の上昇は名目利子率の上昇をもたらし、実質貨幣残高への需要を減少させる。人々は手元に置く貨幣を減らすと、預金を引き出すために銀行に通う回数を増やさなければならない。銀行に足繁く通うことで靴が早く傷んでしまうことを例えて名付けられた。
メニュー・コスト:
高率のインフレによって、企業が価格を頻繁に変更しなければならないことから生じるコスト。価格変更を反映した新しいカタログの印刷や配布、レストランの新しいメニュー表の印刷など。
資源配分の非効率性:
インフレ環境下において、メニュー・コストを原因として企業が価格変更頻度を下げると、同一商品の相対価格がインフレ率に応じて下落していってしまう減少。
課税システムの歪み:
インフレが納税額を変えてしまうこと。
①キャピタルゲイン課税。インフレ率6%の環境で、100ドルで買った株式を1年後に106ドルで売却した場合、実質価値としては利益は出ていないが、課税対象額は6ドルとなる。
②納税ラグ。課税額決定から納税までには一定の期間があるため、高インフレ環境下では課税〜納税までの期間に納税額の価値が減ってしまう。
社会活動の不便さ:
インフレ環境下では、貨幣の機能である「計算単位」が揺らいでしまう。インフレの度合いによっては、他の二つも機能不全に陥る。そこから生じるさまざまな社会的不便さも、インフレのコストであると言える。
<予想外のインフレーションコスト>
住宅ローンや年金が定額であった場合に、予想していた値よりも現実のインフレ率が高くなると、貸し手または借り手が予想外のコストを支払うことになる。
ランクづけは、インフレの度合いによっても変わってくるだろうと思われるため私には不可能。強いて言えば「社会活動の不便さ>その他」。
6)ハイパーインフレーションの発生と終息における、金融政策と財政政策の役割を説明しなさい。
ハイパーインフレは、金融政策によって発生し、財政政策によって終息する。
【発生】
ハイパーインフレの原因はマネーサプライの過剰な成長、すなわち、紙幣増刷の速度が速すぎることにある(金融政策)。
なぜ紙幣増刷の速度が速くなってしまったのかを考えるためには、財政政策に視点を移す必要がある。
ほとんどのハイパーインフレは、税収が足りず、政府が財政支出を賄えないときに発生する。政府は残された唯一の「意のままになる手段」である紙幣の増刷によって赤字を補填する。
【終息】
ほとんどのハイパーインフレは、財政改革によって終焉する。問題の深刻さがはっきりしてくると、政府は政治的意思を結集して、財政支出を減らし、かつ増税する。貨幣発行収入への依存度が軽減され、マネーサプライの成長が減速される。
7)「実質変数」と「名目変数」の定義を述べ、それぞれの具体例をあげなさい。
実質変数:
量や相対価格など、物理的単位で測られるすべての変数。
実質GDPや資本ストック(量)、実質賃金や実質利子率(相対価格)
名目変数:
貨幣を単位として測られる変数。
物価水準、インフレ率、名目賃金
応用問題
1)ウィクナム国では、貨幣の流通速度は一定である。実質GDPは年率3%、貨幣ストックは年率8%増大しており、名目利子率は9%である。次の値はいくらになるか。
a 名目GDPの成長率
b インフレ率
c 実質利子率
Mの変化率 + Vの変化率 = Pの変化率 + Yの変化率(①)
a
名目GDPはPYによって表されるので、①の右辺に等しい。題意よりVは一定のため、8%。
b
題意より、Yの変化率が3%であるため、Pの変化率は、8 - 3 = 5%
c
実質利子率 = 名目利子率 - インフレ率 = 9 - 5 = 4%
2)ある国の貨幣需要関数が、$${(M/P)^d = kY}$$で表されるものとしよう。kは一定のパラメーターである。マネーサプライは年率12%で成長し、実質所得は年率4%で成長しているとする。
a 平均インフレ率を求めなさい。
b 実質所得の成長率がもっと高いとき、インフレ率はどうなるか。理由も説明しなさい。
c kというパラメータは、どのように解釈できるか。貨幣の流通速度との関係はどのようなものか。
d 貨幣需要関数は一定ではなく、貨幣の流通速度が金融革新によってどんどん早まっているとしよう。このことはインフレ率にどのように影響するか。
Mの変化率 + Vの変化率 = Pの変化率 + Yの変化率(①)
a
貨幣の流通速度は一定であるとすると、①より、P = M - Y = 12 - 4 = 8%
b
①とaの仮定より、Yが大きくなるならばPは下がらなければならない。
c
貨幣需要関数において、パラメータkは、所得1ドル当たりどれだけの貨幣を保有したいと人々が考えているかを示している。
貨幣需要関数$${\frac{M}{P} = kY}$$の項を変形すると、$${M(\frac{1}{k}) = PY}$$となる。したがって、貨幣流通速度との関係は、V = 1/kと表せる。
人々が所得1ドルにつき多くの貨幣を保有したい(kが大きい)ときには、貨幣が所有者を変える頻度は低い(Vが小さい)。逆に、人々が所得1ドル当たり少しの貨幣を保有したい(kが小さい)ときには、貨幣が所有者を変える頻度は高い(Vが大きい)。貨幣需要の係数kと貨幣流通速度Vとは、1枚のコインの裏表の関係にある。
d
①においてVが上昇した場合、Yは外生変数であるため、Vの上昇に対応する形でPも上昇する。
3)ある経済の貨幣需要関数が次式で表されるものとしよう。
$${(\frac{M}{P})^d = (0.2Y / i^{1/2})}$$
a 貨幣の流通速度を表す式を導出しなさい。流通速度は何に依存しているか。そのような依存関係が生じる理由も説明しなさい。
b 名目利子率が4%の場合の流通速度を計算しなさい。
c 生産Yが1000単位で、貨幣供給Mが1200ドルのとき、物価水準Pはいくらになるか。
d 新しい中央銀行総裁が発表され、その人がインフレーションに対して厳しくないという評判なので、予想インフレ率が5%ポイントだけ上昇したとしよう。フィッシャー効果の考え方に基づけば、名目利子率はいくらに変化するか。
e 新しい状況に対応して、流通速度はいくらに変化するか。
f 新総裁発表の後、経済の生産も貨幣供給も変化しないとすれば、物価水準はどうなるか。どうしてそうなるのかを説明しなさい。
g 新しい中央銀行総裁が、任命の公表後も物価水準を変化させずに維持したい場合、貨幣供給をどのような水準にしなければならないだろうか。
所得1ドル当たりどれだけの貨幣を保有したいかを定数kで表すこととする。
a
$${\frac{M}{P} = kY}$$なので、$${\frac{M}{P} = \frac{0.2Y}{i^{\frac{1}{2}}}}$$について、
$${kY = \frac{0.2Y}{i^{\frac{1}{2}}}}$$
$${5k = \frac{1}{i^{\frac{1}{2}}}}$$
V = 1/kなので、k = 1/V
$${\frac{5}{V} = \frac{1}{i^{\frac{1}{2}}}}$$
したがって、$${V = 5i^{\frac{1}{2}}}$$(①)
流通速度は名目利子率に依存している。
名目利子率が上がると、預金が増え、現金保有量は減る。現金保有量はパラメータkの定義を反映した結果であり、kの減少は逆数であるVの上昇を意味する。
b
①に4を代入すると、V = 5*2 = 10
c
MV = PY より、
1200V = 1000P
P = 1.2V = $${6i^{\frac{1}{2}}}$$(②)
(bの仮定において名目利子率が4%の場合、P = 12)
d
4 + 5 = 9%
e
5*3 = 15
f
②に i = 9 を代入すると、P = 6 * 3 = 18
説明、、、、実質貨幣残高への需要と供給が等しいことを仮定しているから(説明にはなっていないですが書きようが)。
g
MV = PY において、
MV = 12(維持)* 1000 にしたいという題意なので、
MV = 5M$${i^{\frac{1}{2}}}$$ = 12000
M$${i^{\frac{1}{2}}}$$ = 2400
3M = 2400
M = 800
4)貨幣需要関数が、次式で表されるものとしよう。
$${(\frac{M}{P})^d = L(i, Y)= Y/(5i) }$$
a 生産の成長率がgで名目利子率が一定のとき、実質貨幣残高への需要の伸びを計算しなさい。
b この経済における貨幣の流通速度を示しなさい。
c インフレ率と名目利子率が一定であるとする。貨幣の流通速度が速まるとすれば、その成長率はいくつか。
d 利子率の水準が恒久的に上昇した(1回上昇してそのままの水準にとどまった)とすれば、流通速度の水準にはどのような影響があるか。その後の流通速度の上昇への影響はどのようなものか。
e 中央銀行が長期的なインフレ目標であるπを実現しようとするならば、貨幣供給をどれだけの率で成長させるべきか。
所得1ドル当たりどれだけの貨幣を保有したいかを定数kで表すこととする。
a
$${(\frac{M}{P})^d = Y/(5i)}$$におけるYがg上昇すると、$${(\frac{M}{P})^d}$$もg上昇する。
b
$${\frac{M}{P} = kY}$$において、$${k = \frac{1}{5i}}$$
$${V = \frac{1}{k}}$$なので、
V = 5i
c
V = 5i なので、iが一定であればVも一定。
d
流通速度も1回だけ上昇してその後は変化しない。
e-1
貨幣数量説によればMの増加率 = πなので、貨幣供給もπと同率で成長させればよい。
e-2
題意より$${(\frac{M}{P})^d = L(i, Y)= \frac{Y}{5i}}$$であり、i = r + Eπを代入・Mについて解くと、$${M = \frac{PY}{5(r + Eπ)}}$$となる比率で成長させればよい。
5)かつてある新聞に「アメリカ経済は低率のインフレーションの只中にいる」という記事が出たことがある。その記事には、「インフレ率が低いことには悪い面もある。4500万人に及ぶ公的年金等の受給者は、来年の自分たちの受取額がわずか2.8%しか増えないことになるだろう」と書かれていた。
a 政策立案者が、公的年金などの受取額をインフレーションに連動させているのはなぜか。
b 受取額の増加が小さいことは、この記事の示唆するように低いインフレーションのコストだろうか。判断の理由も説明しなさい。
a
インフレには「予想外のコスト」が存在する。もし公的年金の受取額がインフレに連動していなかった場合、期待インフレ率と実際のインフレ率の差が大きくなった場合に、国または受取者のいずれかが大きな損をすることになってしまう。インフレに連動させることで、年金の実質的な受給額は一定に保持される。
b
インフレ率に連動している限りにおいて、年金の実質的な受給額は変わらない。将来の物価も年金も共に上がった(下がった)場合に受給額で購入できる財・サービスの量は同じである。(したがって受給額の寡多はインフレーションのコストとは言えない)
6)第2次世界大戦中、ドイツとイギリスはどちらも紙の兵器を考えていた。両国とも相手の紙幣を偽造しており、飛行機を使って相手国内に大量散布する計画だったのである。この作戦に効果があるとすれば、それはどのような理由によるだろうか。
もし、仮に、万が一、インフレを起こすレベルで紙幣が散布され、それが実際に国内で流通するようなことが起こったとしたら、復習問題の問5で記述したような各種コストが経済に対して発生することになる。(各種コストによって作戦に効果が生まれる)
7)以下に列挙する諸シナリオに関して、インフレの費用を説明して、分類しなさい。
a インフレ率が高まったので、J.Crew社は、衣料カタログの発行を、四半期から月次に変更することを決定した。
b 祖父は、自分が生きている間毎年1万ドルを受け取れる年金契約を、保険会社から購入した。その購入後、数年のうちに、高率のインフレーションによって物価水準が予想外の3倍になった。
c マリアは、ハイパーインフレーション状態の経済で暮らしている。毎日の給料受け取り後、彼女はできる限り早く店に行く。受け取った貨幣の価値が低下する前に、使おうというのである。
d ジータは、インフレ率が10%の経済で暮らしている。昨年、自分の金融資産(株式と債権)ポートフォリオに対して、彼女は5万ドルの収益を受け取った。彼女の直面する税率は20%なので、彼女は政府に対して1万ドルを税金として支払った。
e あなたの父親が、自分は若いとき1時間当たりわずか4ドルで働いていたと、語った。あなたは1時間9ドルの仕事についているから、幸運だなというのである。
復習問題の問5・応用問題の問5でそれなりに詳しく記述したため、説明は省略。
a
メニュー・コスト。
b
予想外のコスト。祖父が受け取る年金の実質価値が損なわれている。
c
靴底コスト。
d
課税システムの歪み。課税額がインフレの調整を受けていない。
e
社会活動の不便さ。インフレによって受け取る名目賃金の実質価値は変動する。ものすごくざっくり、年率3%のインフレが30年くらい続くと父親よりも不利な時給を受け取っていることになる。
8)経済史家のなかには、金本位制の下では、金鉱山は(1896年のケースのように)長期のデフレーションの後に発見されることが多いと主張する人たちがいる。これが正しいとすれば、その理由は何か。
同じ工程によって産出される(技術革新を考慮しない)金の量が同じだとすると、デフレによって等量あたりの金の価値が上がるため、採掘(鉱山の探索を含めた工程全体として捉えたとき)の採算水準が下がるから。
応用問題(追加)
1)ケーガン・モデルにおいて、マネーサプライが一定率μで成長すると予想される(すなわち、$${E_{m_{t+s}} = m_{t} + sμ}$$)の場合、(A9)式は$${p_{t} = m_{t} + γμ}$$という意味になる。
a この結果を解釈しなさい。
b マネーサプライの成長率μを一定にしたままで、マネーサプライ$${m_{t}}$$が変化すると、物価水準$${p_{t}}$$はどうなるだろうか。
c マネーサプライ$${m_{t}}$$を一定にしたままで、マネーサプライの成長率μが変化すると、物価水準$${p_{t}}$$はどうなるだろうか。
d 中央銀行が貨幣の成長率μを低下させたいが、現在の物価水準$${p_{t}}$$は変えたくない場合、$${m_{t}}$$をどうすればよいか。実際にそうした政策をとる場合、何か問題は生じるか。
e 貨幣需要が期待インフレ率に依存しない(γ = 0)という特殊な場合、これまでの答えはどう変わるか。
$${p_{t}}$$:t期における物価水準の対数値
$${m_{t}}$$:t期における貨幣量の対数値
γ:貨幣需要のインフレ率に対する感応度
a
A9を変形すると、$${m_{t} - p_{t} = -γμ}$$となる。この式は、実質貨幣残高への需要がマネーサプライの成長率に依存していることを表す。
b
γが変化しない場合、$${p_{t}}$$は$${m_{t}}$$に対応し同じ量の変化をする。
c
γが変化しない場合、$${p_{t}}$$はμに対応し同じ量の変化をする。
d
$${m_{t}}$$が上がりμが下がれば$${p_{t}}$$を変えずに目的を達成できる。貨幣量は中央銀行のコントロール下にあるが、γはコントロールできないため、実際に$${p_{t}}$$を一定に保てるかどうかは人々の「信認」による。
e
γ = 0 の場合、$${p_{t} = m_{t}}$$となる。
これまでの答えは、、、設問がμの存在を前提とするものばかりだったのでなんとも、、、。「γが0のときにはケーガン・モデルは貨幣数量方程式に戻る」みたいな話をさせたいのだろうか。
第六章 開放経済
復習問題
1)純資本流出とは何か。貿易収支とは何か。それらはどのように関係しているかを説明しなさい。
S:国民貯蓄
I:国内投資
NX:純輸出(貿易収支):X - IM
X:国内の財・サービスの輸出
IM:輸入品に対する支出
純資本流出:
純資本流出は S - I で表され、自国民が外国に貸した額から自国民が外国から借りた額を差し引いた額に等しい。純資本流出がプラスであれば、自国の貯蓄が投資を上回っており、超過分を外国に貸し付けていることを表す。純資本流出がマイナスであれば、資本流入が生じており、投資が貯蓄を上回り、この投資の超過分を外国からの借入れで賄っている。純資本流出は資本蓄積を賄う国際的な資金の流れを反映する。
貿易収支:
財・サービスの純輸出額(輸出 - 輸入)を表す。純資本流出は貿易収支に等しい(S - I = NX)。
2)名目為替レートと実質為替レートの定義を述べなさい。
名目為替レート:
2国間の通貨の相対価格。
実質為替レート:
2国間の財の相対価格。
$${実質為替レート = 名目為替レート × \frac{外国財の価格}{自国財の価格}}$$
実質為替レートが高いときには、外国財は相対的に高く、自国財は相対的に安くなる。実質為替レートが低いときには、外国財は相対的に安く、自国財は相対的に高くなる。
3)小国開放経済が国防支出を削減すると、貯蓄、投資、貿易収支、利子率、為替レートに何が生じるか。
貯蓄:
国防費は政府購入Gに属するため、政府購入の減少は政府貯蓄ならびに国民貯蓄の増加を意味する。
投資:
投資は世界利子率r*に依存するため、小国開放経済では投資への影響は生じない。
貿易収支:
貯蓄の増加に対応した分、上昇する(NX = S - I)。
利子率:
小国開放経済では世界利子率への影響は生じない。
為替レート:
純輸出の増加により実質為替レートも上昇する。
4)ある小国開放経済が日本のビデオゲームシステムの輸入を禁止すると、その国の貯蓄、投資、貿易収支、利子率、為替レートに何が生じるか。
本章のモデルでは、保護貿易政策(輸入の禁止)は、純輸出(輸出 - 輸入)の需要を増やし、純輸出需要曲線を右方シフトさせる。しかし、貯蓄と投資のいずれにも影響を与えないため、貿易収支(NX = S - I)には変化を与えない。需要曲線のシフトにより、為替レートの均衡点は変化する。
貯蓄:
変化しない。
投資:
変化しない。
貿易収支:
変化しない。
利子率:
変化しない。
為替レート:
実質為替レートは下がる(増価する)。
5)購買力平価説によれば、もし日本のインフレ率が低く、メキシコのインフレ率が高いとき、日本の円とメキシコのペソの間の為替レートには何が生じるか。
名目為替レートeの変化率 = 実質為替レートεの変化率 + (π - π*) なので、標題の場合、日本円が増価する。
応用問題
1)以下の出来事が起こったとき、貿易収支、実質為替レート、名目為替レートに何が生じるかを、小国開放経済モデルを用いて予測しなさい。
a 消費者の将来への不安が増し、支出が減り、貯蓄が増える。
b 税制改革が新しい工場を建設する企業家のインセンティブを高める。
c フォードがすぐれたデザインの新車を発表したため、日本の消費者の関心が国産車から外国車に移る。
d 中央銀行が貨幣供給を2倍に増やす。
e クレジットカードの使用を制限する新しい規制が貨幣需要を増大させる。
S:貯蓄
I:投資
NX:貿易収支 = 純輸出
NX = S - I
実質為替レートは純輸出と正の相関(①)
実質為替レート = 名目為替レート × $${\frac{外国財の価格}{自国財の価格}}$$(②)
a
貿易収支:
Sが増えるので、増える。
実質為替レート:
NXが増えるので、上がる。
名目為替レート:
実質為替レートが上がるので、上がる。
b
貿易収支:
Iが増えるので、減る。
実質為替レート:
NXが減るので、下がる。
名目為替レート:
実質為替レートが下がるので、下がる。
c
復習問題4の逆を考えればよい。純輸出需要曲線は左方シフトする。
貿易収支:
変わらない。
実質為替レート:
上がる。
名目為替レート:
上がる。
d
貨幣数量説(第5章)によれば、マネーサプライが増えると価格が上がる(流通速度や生産量は変化しないものとする)。貯蓄や投資に影響を与えないとすると、
貿易収支:
変わらない。
実質為替レート:
貿易収支が変わらないため、変わらない(①)。
名目為替レート:
②の左辺が変わらず、自国財の価格が上がり、外国財の価格が変わらないため、上がる。
e
クレジットカードの使用が制限されるとマネーサプライは減少するはずなので、その影響力次第。。仮にマネーサプライへの影響がなく、貨幣需要のみが増大したとすると、貨幣需要関数$${\frac{M}{P} = kY}$$におけるMとYが固定されるため、kが上がるならPは下がる。
貿易収支:
変わらない(問dと同じ理屈)。
実質為替レート:
変わらない(問dと同じ理屈)。
名目為替レート:
Pが下がるため、名目為替レートは下がる。
2)次の方程式で表される経済を考えよう。
Y = C + I + G + NX(①)
Y = 8000
G = 2500
T = 2000
C = 500 + 2/3(Y - T)
I = 900 - 50r
NX = 1500 - 250ε
r = r* = 8
a この経済の個人貯蓄、公的貯蓄、国民貯蓄、投資、貿易収支、均衡為替レートを求めなさい。
b Gが2000に削減されたとしよう。個人貯蓄、公的貯蓄、国民貯蓄、投資、均衡為替レートを求めなさい。また、その結果を説明しなさい。
c 世界利子率が8%から3%に下落したとする(Gは2500のままとする)。個人貯蓄、公的貯蓄、国民貯蓄、投資、均衡為替レートを求めなさい。また、その結果を説明しなさい。
C = 500 + 4000 = 4500
I = 900 - 400 = 500
①より、8000 = 4500 + 500 + 2500 + (1500 - 250ε) = 9000 - 250ε
ε = 4
a
個人貯蓄:
Y - T - C = 8000 - 2000 - 4500 = 1500
公的貯蓄:
T - G = 2000 - 2500 = -500
国民貯蓄:
1500 + (-500) = 1000
投資:
500
貿易収支:
NX = S - I = 1000 - 500 = 500
均衡為替レート:
4
b
個人貯蓄:
1500
公的貯蓄:
0
国民貯蓄:
1500
投資:
500
貿易収支:
1000
均衡為替レート:
8000 = 4500 + 500 + 2000 + (1500 - 250ε) = 8500 - 250ε
ε = 2
国民貯蓄が増加したが投資は変わらないため、その分、貿易収支が黒字方向にスライドした。貿易収支の増加は実質為替レートの下落(通貨の減価)を意味する。(章中の図とはそぐわないが、これはP.216の注4で書かれている為替レートの表記問題(米ドル建てか円建てか)によるものだと思われる。日本版にする際に応用問題の関数(NX(ε))もいじっておけばいいのに…)
c
r = 3
I = 900 - 150 = 750
8000 = 4500 + 750 + 2500 + (1500 - 250ε) = 9250 - 250ε
ε = 5
個人貯蓄:
1500
公的貯蓄:
-500
国民貯蓄:
1000
投資:
750
貿易収支:
250
均衡為替レート:
5
金利が下がると投資が増えて貿易収支が減り、実質為替レートは上昇(通貨は増価)する。
3)ラブレ国は小国開放経済である。世界の流行が突然変化して、ラブレの輸出品の人気が低下した。
a ラブレ国の貯蓄、投資、純輸出、利子率、為替レートに何が生じるか。
b ラブレ国の市民は海外旅行が好きだ。この為替レートの変化は彼らにどのように影響するか。
c ラブレ国の政策当局は増税か減税かによって為替レートを元の水準に戻したいと考えている。政策当局はどのようにすべきか。そのとき、貯蓄、投資、純輸出、利子率はどのような影響を受けるか。
a
基本的には復習問題4の(輸出入)逆が起こる。
貯蓄:
変わらない。
投資:
変わらない。
純輸出:
変わらない。
利子率:
変わらない。
為替レート:
実質為替レートが上昇(通貨が減価)する。
b
aの結論から、海外旅行のコストは高くなる。
c
減少により左方シフトした純輸出需要と純輸出NX(= S - I)の交点が元の実質為替レートεと等しくなるような変化が起こればよいので、投資Iが世界利子率によって固定されている前提において、貯蓄Sが減少すればこの変化が実現する。S = Y - C - G であり、YもGも固定されている前提では、C(Y - T)の変化について考えればよい。増税する(Tが増える)とCは小さくなり、減税する(Tが減る)とCは大きくなる。貯蓄Sが減少するには、減税すればよいことがわかる。
貯蓄:
減る。
投資:
変わらない。
純輸出:
減る。
利子率:
変わらない。
4)小国開放経済において、たとえば戦時中のように政府が財の購入を増やすと、小国開放経済の貿易収支と実質為替レートに何が生じるか。あなたの答えは、この戦争が局地戦争であるか世界戦争であるかによって変わるだろうか。
政府購入が増えると国民貯蓄が減少する。したがってNXは減少し、実質為替レートは下落(通貨が増価)する。
貿易収支:
減少する。
実質為替レート:
下落する(増価する)。
局地戦争か世界戦争かによってこの答えは変動する。局地戦争では世界利子率r*への影響は考慮する必要がないが、世界戦争では世界利子率が変動するものとして考える必要がある。
(※局地戦争でも大国の参加など、経済に与えるインパクトが大きい場合は存在し、その場合は世界利子率が変動する可能性がある。)
世界戦争の場合、政府購入の増加は、国民貯蓄の減少を意味する。国民貯蓄が減少すると利子率は上がる。
世界利子率が上がると、国内単位で見ると投資Iの減少に繋がり、純輸出(NX = S - I)の増大ならびに実質為替レートの上昇が起こる可能性がある。
※資源や兵器などの輸入増により、輸入先の貿易相手国を対象とする純輸出に限っては増大しない、もしくは減少する(実質為替レートは上昇しない、もしくは下降する)可能性も考慮できる。
5)本章のケース・スタディでは、貧しい国がより効率的な生産性と法的保護を提供するならば、アメリカのような豊かな国々の貿易収支は黒字の方向に変化するだろうという結論であった。どうしてこのようなことが生じるのか考えてみよう。
a 世界の貧しい国々がより効率的な生産性と法的保護を提供したとき、それらの国の投資需要関数に何が起きるか。
b 問aで述べた変化は、世界の金融市場の貸付資金需要にどのように影響するか。
c 問bで述べた変化は、世界の利子率にどのように影響するか。
d 問cで述べた変化は、豊かな国々の貿易収支にどのように影響するか。
a
「より効率的な生産性」は、$${F(K, L)= AK^{α}L^{1-α}}$$におけるAの増加を意味し、「法的保護」は投資の安全性の向上を意味する。両者は投資需要関数の上方シフト(P.105の図)を起こす。
b
投資需要関数の上方シフトは、利子率の上昇につながり、利子率の上昇は貸付資金需要の上昇をもたらす。
c
bで先回りしてしまったが、世界利子率は上昇する。
d
世界利子率が上がると投資は減り、貿易収支は増加する。
6)アメリカの大統領が日本の高級車の輸入に関税をかけることを考えている。本章で示したモデルを使って、このような政策の政治経済的影響を論じなさい。とくに、この政策がアメリカの貿易赤字にどのような影響を与えるだろうか。為替レートにどう影響するだろうか。このような政策で損失を被るのは誰だろうか。利益を受けるのは誰だろうか。
復習問題4の議論より、貿易赤字に対しては影響を及ぼさず、為替レートは上がる(通貨は増価する)。
保護貿易政策は、貿易収支を変化させることはないが、貿易量には影響を与える。実質為替レートが低下すると、自国の財・サービスは外国の財・サービスと比べて割高となり、輸出量は減少する(輸入量の減少と等量)。
総貿易量の減少は、平均的な社会全体に対して損害をもたらし、国内の自動車メーカーにとっては利益となる。
7)下に4つの仮想的な国(アルファベット順)の通貨に関する表6-2と類似の表がある。購買力平価説を用いて空欄に数値を入れなさい。ただし、与えられた情報から数値が確定しない場合はNAを書き入れなさい。あなたの解答を説明しなさい。

ハグリッド
題意より為替レートはフラッフィ建なので、予測値・現実値ともに1
ハーミオニア
5 * 80 = 400
ポタースタン
60 / 5 = 12
ロンランド
NA
8)中国が人民元を使ってテレビを売り、ロシアはルーブルを使ってウォッカを輸出するとしよう。中国の貨幣供給は安定しており、テレビの生産はゆっくりとではあるが着実な技術進歩を行っている。一方、ロシアは貨幣供給を急速に増やしており、ウォッカの生産に技術進歩はない。これらの情報に基づいて、あなたは実質為替レート(テレビ1台当たりのウォッカの本数)と名目為替レート(1元あたりのルーブル)についてどのように予測するだろうか。またその予測の根拠を説明しなさい(ヒント:実質為替レートについては、希少性と相対価格の関係を考えなさい)。
(そうしないと解けないため)投入する生産要素の量は一定と仮定する。
貨幣供給について、中国<ロシアなので、インフレ率も中国<ロシア(貨幣数量説)。
(実際には生産量Yや流通速度Vの変動次第で影響は未知数だが「急速に」貨幣供給が増えるならある程度正しいと言えそう/生産量の面も中国の方が成長速度が速そうなので相対的なインフレ率の傾斜はより急になるのではないかと思う)
したがって、$${ε = e × \frac{P^*}{P}}$$(①)において、(設題が中国基準なので)$${\frac{P^*}{P}}$$は増大していく。
題意の経済において実質為替レートとは$${\frac{ウォッカの本数}{テレビの台数}}$$(②)のことを指す(③)。生産量について、$${F(K, L)= AK^{α}L^{1-α}}$$におけるAの部分(生産効率)が中国>ロシアであるという題意なので、②の値は徐々に小さくなってゆく。
実質為替レート(ε):
上記より徐々に減少する。
名目為替レート(e):
実質為替レートの下がり方とインフレ格差の上がり方に依存し、$${e = ε × \frac{P}{P^*}}$$の関係で表される。
9)オセアニアは小国開放経済である。外国のたくさんの国が投資税額控除を設けて投資に対する補助を開始する(他方で、それ以外の税を調整して税収は一定に維持する)が、オセアニアはこのような投資補助は行わない。
a 世界利子率の関数である世界の投資需要に何が生じるか。
b 世界利子率に何が生じるか。
c オセアニア内の投資に何が生じるか。
d オセアニアの貿易収支に何が生じるか。
e オセアニアの実質為替レートに何が生じるか。
a
投資需要は増大する。
b
aにより、世界利子率も上昇する。
c
bの影響で投資は減少する。
d
EX = S - I なので、Iが減少すればEXは増大する。
e
貿易収支の増大により実質為替レートは上昇する(通貨が減価する)。
10)友人が「メキシコ旅行は10年前に比べてはるかに安くなった。10年前には1ドルで10ペソしか買えなかったが、今では1ドルで15ペソも買える」といっている。あなたの友人は正しいか、誤っているか。この10年間のアメリカのインフレ率が25%、メキシコのインフレ率が100%とすると、メキシコ旅行は安くなったのか、それとも高くなったのか。アメリカのホットドッグ1個とメキシコのタコス1個のような具体例を用いて、あなたの友人を説得できる答えを書きなさい。
ホットドッグとタコスの例を出すと余計ややこしくなる気がするが、題意に則って整理すると以下のようになる。

メキシコでのインフレの進行により、メキシコで$1あたり購入可能な財・サービスの量は減っており、友人は誤っていると言える。
11)金融に関するWebサイトでカナダの名目利子率は年12%、アメリカの名目利子率は年8%であることを知った。実質利子率は両国で等しく、購買力平価説が成り立つと仮定する。
a (第5章で議論した)フィッシャー方程式を用いると、カナダとアメリカの期待インフレ率についてどのようなことがいえるか。
b カナダ・ドルと米ドルの間の為替レートの変化についてどういう予測ができるか。
c 友人が一攫千金の計画を提案している。アメリカの銀行から8%でお金を借り、それをカナダの銀行に12%で預金することで、4%の儲けを得るというのである。この計画はどこが間違っているか。
a
フィッシャー方程式:
名目利子率をi、実質利子率をr、インフレ率をπとしたとき、
i = r + π
題意より実質利子率は両国で等しいため、
「カナダの期待インフレ率 - アメリカの期待インフレ率 = 4%」
といえる。
b
eの変化率 = εの変化率 - (π - π*) であり、(π - π*) がaで示されたので、
「eの変化率 = εの変化率 - 4%」
と予測できる。
c
a、bより、名目為替レートの変化率と受け取れる金利差が等しい状況であれば、友人の計画は利益を産まない。
応用問題(追加)
1)もし外国で戦争が勃発すれば、多くの経路を通じてアメリカ経済に影響が及ぶだろう。このような戦争の影響を調べるために、大国開放経済モデルを用いる。以下の場合、アメリカ国内で、貯蓄、投資、貿易収支、利子率、為替レートに何が生じるか(問題を簡単にするために、それぞれの影響を別々に考えなさい)。
a アメリカ政府が戦争突入に備えて、軍需品の購入を増やす。
b 外国がアメリカの主要輸出品であるハイテク兵器への需要を増やす。
c 戦争のためにアメリカ企業の将来見通しが不確実になり、企業はいくつかの投資計画を繰り延べる。
d 戦争によってアメリカの消費者が将来に不安を感じ、それに対応して貯蓄を増やす。
e アメリカ人が外国旅行を控えるようになり、アメリカ国内で休暇を過ごす人が増える。
f 海外の投資家が資産の安全な避難場所をアメリカに求める。
※アメリカの話なのでNX曲線の傾きが変わる点に注意(これは次の設問も)
a
前提として、第三章で用いていた以下のモデルを想定する。
国民貯蓄 = Y - C - G = 民間貯蓄 + 公的貯蓄
民間貯蓄 = Y - T - C
公的貯蓄 = T - G
題意は政府購入の増加=国民貯蓄の減少と読み替えられる。

貯蓄
減少する。
投資
減少する(貯蓄の減少により利子率が上昇するとIとCFはともに減少)。
貿易収支
悪化する。
利子率
上昇する。
為替レート
上昇(増価)する。
b
題意は純輸出需要の増加と読み替えられる。
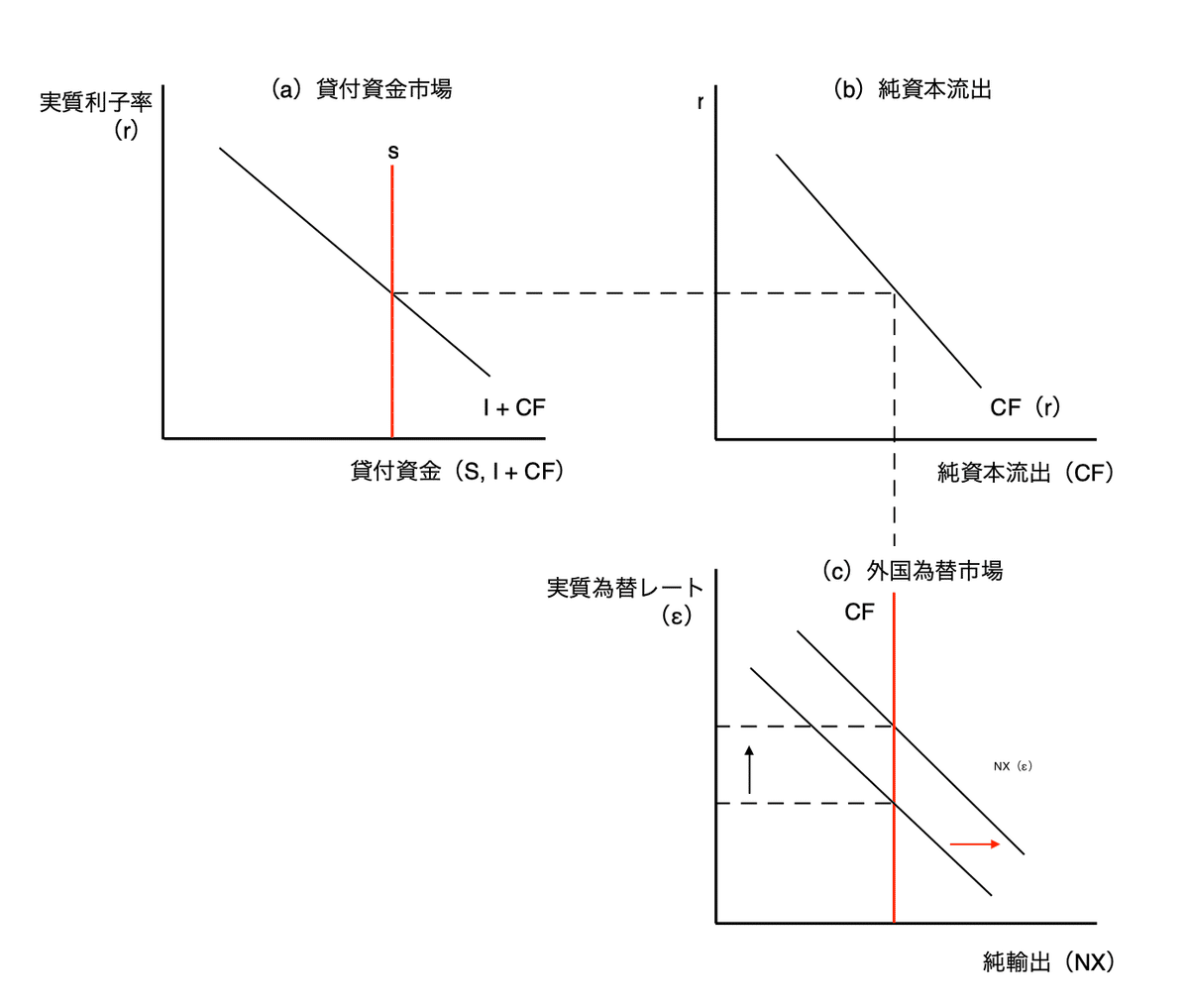
貯蓄
変わらない。
投資
変わらない。
貿易収支
変わらない。
利子率
変わらない。
為替レート
上昇(増価)する。
c
題意は投資需要の減少と読み替えられる。

貯蓄
変わらない。
投資
減少する(I + CFが一定、CFは増加、同量のIが減少)。
貿易収支
改善する。
利子率
下がる。
為替レート
下降(減価)する。
d
これはそのまま(解釈を必要としない)。

貯蓄
増加する。
投資
増加する(IもCFも増加)。
貿易収支
改善する。
利子率
下がる。
為替レート
下降(減価)する。
e
外国旅行による財・サービスの消費はGDPのカウント対象(輸入)であり、題意の外国旅行控えは、純輸出需要の右方シフト(輸入需要の減退)を意味する。これは問bの状況と同じである(図も問b参照)。
貯蓄
変わらない。
投資
変わらない。
貿易収支
変わらない。
利子率
変わらない。
為替レート
(上昇)増価する。
f
題意はCF関数の左方シフトと読み替えられる。

貯蓄
変わらない。
投資
増加する(利子率が下がりI + CFが一定、Iは増加、同量のCFが減少)。
貿易収支
悪化する。
利子率
下がる。
為替レート
上昇(増価)する。
2)1995年9月21日、「下院議員のニュート・ギングリッチ(Newt Gingrich)氏はアメリカの歴史始まって以来の債務不履行に追い込まれる恐れがあると話し、クリントン政権に共和党政権時代の均衡予算に戻るように強く促した」(『ニューヨーク・タイムズ』1995年9月22日)。その日のうちに、30年物の政府国債の利子率は6.46%から6.55%に上昇し、ドル価値は102.70円から99.00円に下落した。大国開放経済モデルを使って、この出来事を説明しなさい。
1)fの逆の現象(アメリカからの資産退避)と、国債の買い控え(=リスクプレミアムの上昇)が起きる。

債務不履行のリスクと投資控えから利子率は上昇し、米国外への資産退避も伴い純資本流出は増える(Sは一定、Iは減るのでCFは増え、CF関数が右方シフトする)。その結果、実質為替レートは減価(下落)する。
第七章 失業と労働市場
復習問題
1)自然失業率を決定するものは何か。
離職率と就職率。
離職率:
就業者の中で1ヶ月間に離職する人の比率
就職率:
失業者の中で1ヶ月間に就職する人の比率
労働力をL
就業者をE
失業者をU
離職率をs
就職率をf
としたとき、
自然失業率$${\frac{U}{L} = \frac{s}{s + f}}$$
と表すことができ、
・離職率が高くなれば失業率は高く
・就職率が高くなれば失業率は低く
なる。
2)摩擦的失業と構造的失業との違いを説明しなさい。
摩擦的失業とは、求人と求職者のマッチングに時間がかかることで発生する失業を指す。仕事口には給与や要件などの差異があり、労働者には選好がある。求人情報の流れは瞬時ではなく、適切な職を探すことは、時間と労力を要求する。
構造的失業とは、賃金の硬直性と職の割り当てによって生じる失業を指す。「構造」とは、現行の賃金水準において、労働供給が労働需要を上回っている状況。この場合、多くの失業者は自分に職が割り当てられるのを待つことしかできない。構造的失業が発生する理由は、労働の超過供給が発生しているにもかかわらず、企業が何らかの理由で賃金を引き下げないことである。
賃金の硬直性:
労働需要と労働供給が一致するところまで賃金が調整されないこと。
3)実質賃金が労働市場の需給均衡水準を超えて高止まりすることについて、3種類の説明をしなさい。
最低賃金法
企業が労働者に支払う賃金の法的下限を設定すること。一部の労働者、とくに未熟練労働者や就業経験の浅い人々の賃金は、最低賃金法によって均衡水準以上に引き上げられる。
労働組合の独占的交渉力
組合に加入している労働者の賃金は、市場の需要均衡ではなく、労組指導者と企業経営陣との間の団体交渉によって決定される。賃金は最終合意によって均衡水準以上に押し上げられる。また、組織化されていない労働者の賃金においても、労働組合の結成を恐れる企業は、賃金を均衡水準よりも高めに設定する傾向がある。
効率賃金
効率賃金仮説では、高賃金を支払うことで労働者がより生産的になると考える。賃金が労働者の生産性に影響する場合、労働の超過供給があっても企業は賃金を引き下げない可能性がある。
(以下は仮説)
①発展途上国では、賃金水準が栄養摂取量に影響する。
②高給によって、離職率が下がる(新規雇用や訓練コストの削減)。
③労働者の質の平均水準は賃金に依存する(高給は逆選択の回避になる)。
④高給は労働者の労働意欲を高める(労働者の解雇コストを上げる)。
企業は高賃金を支払うことによって経営効率を高めることができるので、賃金を均衡水準以上に維持することは企業にとってプラスとなりえる。
4)失業のほとんどは短期的なものだろうか、それとも長期的なものだろうか。答えを述べ、その理由を説明しなさい。
失業件数をみるか、失業期間総数をみるかによって、失業の過半は短期にも長期にも変わる。失業件数のほとんどは短期間のうちに終了するが、失業期間総数(失業期間×人数の総和)のほとんどは長期失業者で占められる。
5)ヨーロッパの人々は、アメリカ人と比べてより長く働いているだろうか、あるいはより短く働いているだろうか。両者の間の相違を説明する3つの仮説を説明しなさい。
ヨーロッパの人々は、アメリカ人と比べて、より短く働いている。
①税制の相違
(1)ヨーロッパ人はアメリカ人よりも税率が高い
(2)ヨーロッパの税率は、ここ数十年で大きく引き上げられた
税金は労働に影響する。
また、税率が高いと、人々は税金を免れるため、帳簿外で働くことがある。地下経済における労働は、労働時間に集計されないため、実際の労働時間の相違は、計測された労働時間の相違よりも小さい可能性がある。
②労働組合の役割
アメリカよりもヨーロッパの方が労働組合の組織化率が高く、労働組合は、労使交渉において労働日数の削減を要求したり、休日の新設をはじめ、さまざまな労働市場規制を政府に働きかける。休日の相違は欧米間の勤労週数の相違の80%を説明できる。
③選好の相違
技術進歩と経済成長は先進国を豊かにしたが、アメリカでは、その豊かさ(生産性の向上)を、所得を増やすこと(より多くの財・サービスの消費)に、ヨーロッパでは、余暇を増やすことに用いたという選好の相違がある。
応用問題
1)自分の労働経験に基づいて下記の問いに答えなさい。
a あなたや友達がパートタイムの仕事を見つけるまで、通常は何週間くらいかかるか。またそうした仕事は何週間ぐらい続くか。
b あなたの経験に基づいて、自分の就職率fと離職率(1週間当たりの率)を計算しなさい(ヒント:就職率がfであれば、平均的な失業期間は1/fになる)
c あなたの属する人口グループの自然失業率を算出しなさい。
久々になんとも言えない問題きましたね…一章の床屋を思い出しました。
a
Google先生によるとこんな感じ。サンプル数や調査サイトによっても差があるので微妙なところですが。バイト・パートの場合、喫緊でお金が必要な人が応募しやすかったりしそうな(求職期間が短い)感じに見えますね。1~3年の継続層が思ってたより多かったのは意外でした。


b
仮に求職期間を2週間、勤続期間を半年とすると、1週間当たりの就職率fは1/2。1週間当たりの離職率sは1/24。
c
仮にbの例を用いると、自然失業率$${\frac{U}{L} = \frac{s}{s + f} = \frac{\frac{1}{24}}{\frac{1}{24} + \frac{1}{2}} ≒ 0.077 = 7.7%}$$
2)ある寮に住む学生たちが、次のような調査をしたとしよう。寮生を恋人がいる人といない人に分けたところ、恋人がいる人のうち毎月10%の人が別れていた。また恋人がいない人のなかで毎月5%が新たな交際を始めていた。この寮生たちの恋人がいない人の比率の定常状態値を求めなさい。
普通に自然失業率の例でいいじゃないですか…どうして…
$${\frac{U}{L} = \frac{s}{s + f} = \frac{0.1}{0.1 + 0.05} ≒ 0.667 = 66.7%}$$
3)本章では、定常状態における失業率が U / L = s / (s + f) であることを学習した。当初の失業率がこの水準から乖離しているとしよう。失業がどのように変化して定常状態に到達するのかを示しなさい(ヒント:失業者数の変化分を s, f, U の関数で表しなさい。そして、失業率が自然失業率を超えていれば失業が減少し、逆ならば失業が増大することを示しなさい)。
イメージがつかなかったため、任意の数値を入れて試してみたところ下図のような結果が得られた。

ヒントの「失業者数の変化分」は、「sE - fU」で表すことができる。
sとfは固定されているとすると、
・均衡状態においてはsE - fU = 0(sE = fU)
・Eが理論値よりも大きければsE - fU>0
・Eが理論値よりも小さければsE - fU<0
である。
また、E + U(= L)は固定されているとすると、
・Eが大きくなるほどUは小さくなり(結果、sEが増加しfUが減少する)
・Eが小さくなるほどUは大きくなる(結果、sEが減少しfUが増加する)
ことから、乖離が大きければ大きいほど|sE - fU|も大きく変化(乖離縮小圧力が大きく変化)し、定常状態に到達すると言える。
4)企業が雇用者を解雇しにくくなるような法律が、国会で成立したとしよう(たとえば、解雇された労働者に対する退職金の支払いを義務づける法律)。この法律が、就職率を変化させずに離職率だけを低下させた場合、自然失業率はどう変化するか。この法律は就職率を変化させないと考えてもよいか。なぜそうなるかも説明しなさい。
$${\frac{U}{L} = \frac{s}{s + f}}$$において、fが変わらずsが下がる場合、失業率は下がる。
仮に離職率が顕著に下がるとすると、労働需要は減少すると考えられるため、それに応じて就職率も下がることが予想される。
5)次式のようなコブ=ダグラス型生産関数を持つ経済を想定しよう。
$${Y = 5K^\frac{1}{3}L^\frac{2}{3}}$$(①)
a この経済における労働需要関数を、実質賃金と資本ストックの関数として求めなさい(ヒント:第3章を参照すること)。
b この経済には、2万7000単位の資本と1000人の労働者からなる労働力が存在しているものとする。労働の需要と供給が均衡するように実質賃金が調整されるものとしよう。実質賃金、生産、労働者の総所得を計算しなさい。
c 労働者の厚生を考慮して、(あなたが問bで計算した)均衡賃金よりも10%高い最低賃金を、国会が制定したとしよう。この義務づけられた賃金の下で企業がどれだけの労働者を雇用するかについて、国会は干渉できないとしよう。その場合、この法律の影響はどのようなものになるか。実質賃金、雇用、生産、労働者の総所得はどうなるか、具体的に計算しなさい。
d 国会は、労働者を助けるという所期の目的を達成できるだろうか。理由も説明しなさい。
e この分析は、最低賃金法について考察するよい材料となっているだろうか。理由も説明しなさい。
a
競争的な利潤最大化企業を想定した際、労働者に支払われる実質賃金はMPLに等しかった。したがって、
$${\frac{W}{P} = MPL}$$
である。また、コブ=ダグラス関数における労働の限界生産力は、
$${MPL = (1 - α)AK^αL^{-α}}$$
で表された。したがって、
$${(1 - α)AK^αL^{-α} = \frac{W}{P}}$$
$${\frac{10}{3}K^\frac{1}{3}L^{-\frac{1}{3}} = \frac{W}{P}}$$(②)
b
K = 27000
L = 1000
実質賃金
②のKとLに題与の数値を代入すると、
$${\frac{W}{P} = \frac{10}{3}27000^\frac{1}{3}1000^{-\frac{1}{3}}}$$
$${= \frac{10}{3}*30*0.1 = 10}$$
生産
①のKとLに題与の数値を代入すると、
$${Y = 5*27000^\frac{1}{3}1000^\frac{2}{3}}$$
$${= 5*30*100 = 15000}$$
労働者の総所得
労働者への総支払額は「MPL * L」であり(1 - α)Y であるので、
10*1000または15000*2/3で算出され、いずれも10000。
c
最低賃金が10%上昇したとしてWの総額が10%増えるわけではない気はするのですが、そうすると解けなくなりそうなので、
実質賃金
10*1.1 = 11
雇用
Kが変動しないとすると、②より、
$${\frac{10}{3}*30L^{-\frac{1}{3}} = 11}$$
$${L^{\frac{1}{3}} = \frac{100}{11}}$$
$${L = (\frac{100}{11})^3 ≒ 751}$$
生産
①より、
$${5*30*((\frac{100}{11})^3)^{\frac{2}{3}} ≒ 12,397}$$
労働者の総所得
$${11*(\frac{100}{11})^3 ≒ 8,264}$$
d
(他の変数が一定であるという前提のもとで)雇用も労働者の総所得も減っているので、達成できていないと言える。
深読みするのであれば、インサイダーとアウトサイダー問題にもつなげられる(すなわち、インサイダーには利益がありアウトサイダーは損害を受けているとも読める)
e
題与のような(コブ=ダグラス関数を持つ経済における)モデルにおいては、最低賃金法が必ずしも労働者全体の厚生には寄与しないという示唆を得られる点において、この分析は最低賃金法について考察するよい材料となっていると言える。
6)ある国が生産性の低下に見舞われたとしよう。生産関数に何らかのマイナスのショックが生じたのである。
a このとき、労働需要曲線はどうなるか。
b 労働市場がつねに均衡状態に保たれている場合、この生産性の変化は労働市場における雇用、失業、実質賃金にどのような影響を与えるか。
c 労働組合の存在によって実質賃金が一定に保たれている場合、この変化は労働市場にどのような影響を与えるか。
a
競争的な利潤最大化企業による各生産要素の需要量は、収入と調達費用が均衡するまでであった(第三章復習問題2)。生産関数にマイナスのショックが生じると、収入が減る。このため、需要曲線は下方シフトする。
b

雇用
変化しない。
失業
変化しない。
実質賃金
減少する。
c

雇用は←のように減少し、失業は↔︎の量発生する。
7)製造業とサービス業という2部門からなる経済を考えてみよう。製造業とサービス業との労働需要が、以下の方程式で表されるものとしよう。
$${L_m = 200 - 6W_m}$$(①)
$${L_s = 100 - 4W_s}$$(②)
Lは(労働者の人数で測った)労働、Wは(ドルで測った)賃金、下付き添字は部門を表している。経済には100人の労働者がいて、どちらの部門でも働けるし、働く意欲もあるものとしよう。
a 労働者が両部門間を自由に移動できるものとすると、WmとWsとの関係はどのようなものになるか。
b 問aの関係が成立しており、かつ、賃金は労働の需給を均衡させるように調整されるものとしよう。両部門の賃金と雇用を計算しなさい。
c 製造業において労働組合が結成されて、製造業の賃金を25ドルに増やしたとしよう。製造業の雇用を計算しなさい。
d 製造業で労働組合が結成された後、組合の高給職に就けない人々は全員サービス業に移ったとしよう。サービス業の賃金と雇用を計算しなさい。
e 労働者の留保賃金が15ドルであるものとしよう。つまり、15ドル以下の仕事に就くよりは、組合の25ドルの職が空くのを待つことを選ぶのである。各産業における賃金と雇用を計算しなさい。経済の失業率はいくらになるか。
a
Wm = Wsになる。
b
aよりWm = Wsであり、経済に100人の労働者がいることから、
$${L_m + L_s = 100 = 200 - 6W_m + 100 - 4W_s}$$なので、
$${100 = 300 - 10W}$$
$${W = 20}$$
製造業
賃金:$20
雇用:80人
サービス業
賃金:$20
雇用:20人
c
①のWmに25を代入すると、雇用は50人。
d
cより雇用は50人(100 - 50)。
②のLsに50を代入すると、賃金は$12.5。
e
製造業
賃金:$25
雇用:50人
サービス業
賃金:$15
雇用:②のWsに15を代入すると、40人。
失業率
10 / 100 = 10%
8)賃金が上昇すると、労働者はどれだけ働くかを決めるにあたって、(ミクロ経済学の講義で学んだように)逆方向に働く2つの影響を受ける。所得効果は、労働時間を減らす方向の効果である。所得が高まると、より多くの余暇を消費することができるようになるからである。代替効果は、労働時間を増やす方向の効果である。1時間多く働くことの報酬が増価する(すなわち、余暇の機会費用が上昇する)からである。これらの概念を、欧米間の余暇選好の相違に関するブランシャールの仮説に適用しなさい。所得効果が代替効果よりも大きいと思われるのは、アメリカとヨーロッパのどちらか。2つの効果がほぼ相殺されていると思われるのはどちらか。地域によって余暇の選好が異なるという仮説を、あなたは妥当なものと考えるだろうか。理由も説明しなさい。

とりあえず章中にも登場していた推移データを引用。引用先はマンキューとは数値が違いますが算出方法によるものだと思われます(参照先OECDなのは一緒)。大体のトレンド感は合ってるので資料としてはよさそう。
所得効果が代替効果よりも大きいと思われるのはヨーロッパ。生産性の向上が余暇へと流れていることが窺われる。
2つの効果がほぼ相殺されていると思われるのはアメリカ。どちらかの効果の方が大きければ(ネット)、いずれかの方向に明確なトレンドができるはずだが、大まかに横ばいなので、余暇を増やす層と労働時間を増やす層が拮抗していることが窺われる。
地域によって余暇の選好が異なるという仮説の妥当性はなんとも言えない。他の変数よりも説明力が高いかどうかを判断することができない。
9)どの都市にもつねに空きオフィスは存在する。この空きオフィスはいわば失業している資本(遊休資本)である。この現象をあなたはどのように説明するか。失業の説明のうちどのアプローチが、遊休資本の説明に最も適しているだろうか。遊休資本は社会問題だろうか。自分の解答を説明しなさい。
摩擦的失業・レンタル料の硬直性を起因とする構造的失業のいずれのアプローチも、遊休資本の存在を説明するのに適している(より説明力があるのは摩擦的失業と思われる)。
摩擦的失業では、求人と求職者のマッチングに時間がかかることを指摘した。業種や規模によって必要なオフィスの立地・レンタル料・広さなどの選好があり、また、賃貸情報の流通も一瞬ではない。
構造的失業では、賃金の硬直性と職の割り当てによって生じる失業を指摘した。オフィスのオーナーにとって市場価格でレンタルを行うことが魅力的でない事情がある場合、その分のプレミアムを上乗せする可能性がある。
ごく短期的に見れば、資本は常に活用されている方が総生産に寄与するため、社会問題であると言える。
いちおう反例も挙げておくと、遊休資本が全く存在しない均衡市場においては、新規産業に最もフィットしたオフィスを調達するコストが上がり、結果として総生産を削る可能性もある(すごく低い可能性かもしれない)。
第三部 景気循環理論:短期の経済
第八章 景気変動へのイントロダクション
復習問題
1)景気後退期に実質GDPが低下すると、通常では消費、投資、失業率はどうなるか。
消費と投資は成長率が低下する。ただし、投資は消費に比べてはるかに変動が大きい。失業率は通常、高まる。
2)短期においては硬直的だが、長期においては伸縮的になる価格の例をあげなさい。
(日本における)チェーン店のメニュー。
3)総需要曲線が右下がりになる理由を説明しなさい。
・数量方程式MV = PYにおいて、MVが固定されている場合、Pが大きくなればYは小さくなり、Pが小さくなればYは大きくなる。
・物価水準が上昇すると、個々の取引により多くの貨幣が必要になるため、取引の回数や財・サービスの購入量は減少する。
・生産量が増大すると、実質貨幣残高M/Pへの需要が大きくなる。Mが固定されている場合、M/Pが増大するためにはPは小さくなる。(Pが小さくなった場合、実質貨幣残高が増大するため、より多くの生産が需要されるようになる)
総需要:
生産物への需要量と一般物価水準との関係。
総需要曲線:
所与の物価水準の下で人々がどれだけの財・サービスを購入したいか。
4)マネーサプライの増加の影響を、短期と長期に分けて説明しなさい。
マネーサプライが増大すると、総需要曲線は上方シフトする。その影響は以下のように表すことができる。
短期(A → B)
総需要の増大は生産量を増やし、好景気を生み出す。前と同じ価格で、企業はより多くの製品を販売できるようになる。企業は新規雇用を増やし、超過労働(残業)を増やし、工場や機械設備の稼働率を高める。
長期(B → C)
時間が経過するにつれて、高水準の総需要は賃金や物価を引き上げる。物価水準が上昇するにつれて、生産量は減少し、次第に経済は生産量の自然率水準に戻っていく。
5)中央銀行にとって、供給ショックよりも需要ショックの方が対応しやすいのはなぜか。
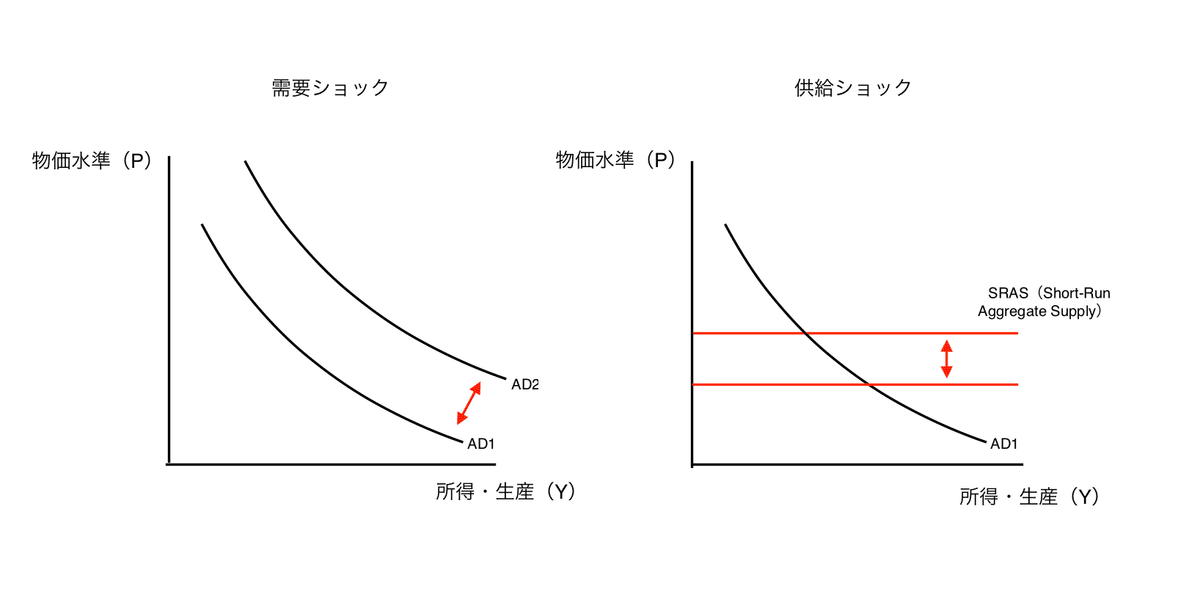
中央銀行に可能な操作は、マネーサプライのコントロールにより総需要を増減させることである。したがって、総需要曲線のシフトである需要ショックに対しては、マネーサプライをうまくコントロールすることができれば、需要ショックの影響を減らしたり除去することが可能である。
一方、短期総供給曲線をシフトさせる供給ショックに際しては、総需要の増減の操作では、完全雇用の維持と物価水準の安定を両立することはできない。中央銀行は、2つの政策のいずれか(完全雇用の維持と物価水準の安定のどちらを短期的に優先するか)を選択することとなる。
1つは、総需要を一定(ショック前の値)のままに保つこと。(不利な供給ショックの場合)短期的に生産量と雇用量が減少し、自然率水準を下回るが、最終的には、長期総供給曲線との交点に収束する(物価水準が元に戻る)。
もう1つは、総需要を増減させることで生産量(雇用量)への影響を減らすこと。長期総供給曲線との交点は上下に移動するため、生産量(雇用量)は守られるが、物価水準への影響は残ってしまう。このような場合、「中央銀行は供給ショックを受容した」と表現する。
供給ショック:
財・サービスの生産費用を変化させ、その結果として企業の製品価格も変更させるような経済へのショック。供給ショックは物価水準に直接的な影響を及ぼす。
需要ショック:
総需要曲線をシフトさせるショック。
応用問題
1)長期均衡の状態において、政府が規制を変更したため、銀行は小切手勘定の預金に利子を付けられるようになったとする。貨幣ストックは現金と要求払い預金との合計額であり、小切手勘定も含まれることを思い出そう。したがって、この規制変更は、貨幣の保有の魅力を高める。
a この規制の変更は、貨幣需要にどう影響するか。
b 貨幣の流通速度はどう変化するか。
c 中央銀行がマネーサプライを変化させないとき、生産と物価は短期と長期ではそれぞれどうなるか。
d 中央銀行の目標が物価水準を安定化させることであるとしよう。この規制変更に対して、中央銀行はマネーサプライを一定に維持するべきか。そうでないとすれば、中央銀行はどうすべきか。理由もあわせて答えなさい。
e 今度は、中央銀行の目標が生産水準を安定化させることであるとしよう。あなたの問dに対する答えはどう変わるか。
※本文をそのまま記述しましたが、小切手決済に手数料がかかるようになったものと理解します。
a
貨幣需要は増加する。
b
貨幣流通速度V = 1/k(kは貨幣需要)だったので、貨幣需要が増加すると流通速度は減少する。
c
MV = PYにおいて、Mが変化せずVが減少するとPYは減少する。
すなわち、総需要曲線は下方シフトする。

短期(B)
生産:減少する。
物価:変わらない。
長期(B→C)
生産:長期総供給曲線との交点に向かって収束し、増加していく。
物価:長期総供給曲線との交点に向かって収束し、下がっていく。
d
この規制は需要ショックであり、中央銀行は総需要が元の曲線に戻る水準を目標にマネーサプライを増やすべき。理由は復習問題5で詳述しているため略。
e
短期的には増やすべきだが、長期的にはどのような操作を行なっても生産には影響を与えない。
2)中央銀行がマネーサプライを5%減少させたとしよう。貨幣の流通速度は一定のままであるものとする。
a 総需要曲線はどうなるか。
b 生産と物価の水準は短期と長期でそれぞれどうなるか。具体的な数値で答えなさい。
c 問bへの解答に基づいて、オークンの法則を適用すれば、短期と長期の失業率がどうなるかを説明しなさい。具体的な数値で答えなさい。
d 実質利子率への影響を、短期と長期とに分けて論じなさい(ヒント:実質利子率に関する第3のモデルを使って、生産水準が変化したときに何が起こるかを調べなさい)。変化の方向だけを答えればよい。
a
下方シフトする(MV = PY、V固定M減少)。
b
Mが5%下がるとPYも5%下がる。

短期(B)
生産:5%減少する。
物価:変わらない。
長期(B→C)
生産:長期総供給曲線との交点(元の値)に向かって収束していく。
物価:長期総供給曲線との交点(元の値よりも5%低い値)に向かって収束していく。
c
短期
失業率の変化率を仮にUとすると、 -5 = 3 - 2U なので、これを整理し、U = 4%(=4%上がる)。
長期
長期的には元の値に戻る。
オークンの法則:
失業とGDPの間に負の相関関係(一方の値が大きくなるほど、他方の値が小さくなる関係)があること。実質GDPの変化率 = 3% - 2 * 失業率の変化。
d

短期
S = Y - C - Gであり、CとGに変化がないとすると、Yが減少するとSも減少する。Sの現象はrの上昇を招く。
長期
長期的には元の値に戻る。
3)中央銀行の政策目標によって、ショックに対する中央銀行の反応がどのような影響を受けるかを検討しよう。Aシナリオにおいて中央銀行は物価安定のみを目標とし、Bシナリオにおいて中央銀行は生産と雇用とを自然率水準に維持することのみを目標としているとする。次のショックに対して、それぞれのシナリオにおいて中央銀行がどのように対応するかを説明しなさい。
a 貨幣の流通速度の外生的な低下
b 原油価格の外生的な上昇
a
MV = PYにおけるVの低下なので、需要ショックにあたる。

Aシナリオ
短期ではなにもしなくてOK、長期ではマネーサプライの増加によって元の水準まで総需要を増加させる対応をとる。
Bシナリオ
短期〜中期ではマネーサプライの増加によって元の水準まで総需要を増加させる対応をとる。長期ではどのような操作を行なっても生産・雇用には影響を与えない。
b
問題設定は「不利な供給ショック」にあたる。

Aシナリオ
中央銀行にできることは、総需要を一定(ショック前の値)のままに保つ対応をとる。長期的には、物価水準は元の水準に戻る。
Bシナリオ
マネーサプライの増加によって総需要を増加させることで、生産・雇用を元の水準に保つ対応をとる。
4)景気後退の開始時点と終了時点を公式に認定しているのは、NPOの経済研究機関である全米経済研究所(NBER)である。NBERのHP(https://www.nber.org/)を訪れて、景気循環の直近の転換点を調べなさい。それはいつか。拡張から縮小への転換点か、その逆だったか。あなたが生まれてからのすべての景気循環をリストアップして、それぞれの開始時点と終了時点を調べなさい〔訳者注:日本における同様のデータは内閣府経済社会総合研究所のHP(https://www.esri.cao.go.jp/)から得られる〕。


2020年の1Q〜2Qでしょうか…? 拡張から縮小への転換点。ただし、2020年のリセッションに関しては、縮小局面が始まった「後」にリセッション認定されている気もします。生まれてからの話は省略します。
NBERのサイトではリセッション表記にナチュラルに失業率がくっついていますが、失業とインフレの関係のような話は12章で言及されます。
第九章 総需要Ⅰ:IS-LMモデルの構築
復習問題
1)ケインジアンの交差図を用いて、財政政策が国民所得に対して乗数効果をもつ理由を説明しなさい。
ケインジアンの交差図とは、家計・企業・政府の財・サービスに対する現実支出(支出する額)と計画支出(支出したい額)が等しいとき、経済が均衡していることを仮定するモデルであった。

ここで、財政政策により政府購入(G)の量や租税(T。CはC(Y - T)の消費関数によって決定されるためCに影響)が増減すると、計画支出が上下にシフトし、均衡所得の交点が変わる(国民所得に対して影響を与える)。
交点の変化がどの程度なのかは以下に示される。
政府購入
政府購入の増加は所得(①)の増加をもたらし、所得(①)の増加によって消費(②)が増える。増えた消費(②)により所得(③)が増加し、増加した所得(③)は消費(④)を増やす…というフィードバックが無限に続く。この無限のフィードバックにより乗数効果が生まれる。
仮に増減した政府購入をΔGとすると、その影響で増減する消費はΔG × MPC、さらにその影響で増える消費は(ΔG × MPC) × MPC…と、政府購入の増加により増減する所得の合計は無限等比数列の和として表され、
$${\frac{ΔY}{ΔG} = \frac{1}{1 - MPC}}$$
と整理することができる。これが政府購入乗数となる(政府購入の差分よりも所得への影響が大きくなる=乗数効果が生まれる)。
租税
同様に、租税乗数は
$${\frac{ΔY}{ΔT} = -\frac{MPC}{1 - MPC}}$$
と整理される。
2)流動性選好理論を用いて、マネーサプライの増加が利子率を低下させる理由を説明しなさい。この説明は物価水準についてどのような仮定をしているか。
流動性選好理論とは、「実質貨幣残高の需要と供給が利子率を決定する」ことを示した理論。ここでは、実質貨幣残高の供給が一定である(物価水準が固定されている)ことを仮定した。

上図においてマネーサプライが増加し、物価水準が固定されているとすると、供給が右方シフトする。結果、需要曲線との交点は右下にシフトし、均衡利子率は下がる。
3)IS曲線はなぜ右下がりなのか。
IS曲線とは、投資関数で表されるrとIとの相互作用と、ケインジアンの交差図で表されるIとYとの相互作用を結びつけたものである。IS曲線は財・サービス市場の均衡(ケインジアンの交差図)と整合的な利子率と所得水準の組み合わせを示す。

r1 → r2| I(r1)→ I(r2)|Y1 → Y2
(a)利子率が上昇すると計画投資が減少する。
(b)計画投資が減少すると計画支出が減少し、下方シフトする。その結果、所得が減少する。
(c)それをプロットしたもの
r1 → r3| I(r1)→ I(r3)|Y1 → Y3
(a)利子率が下降すると計画投資が増加する。
(b)計画投資が増加すると計画支出が増加し、上方シフトする。その結果、所得が増加する。
(c)それをプロットしたもの
上記のように、所得水準と利子率の関係をIS曲線に表すと右下がりとなる。
4)LM曲線はなぜ右上がりなのか。
LM曲線とは、さまざまな所得水準に対して貨幣市場の均衡をもたらす利子率を表したものである。LM曲線は実質貨幣残高市場の均衡と整合的な利子率と所得水準との組み合わせを示す。

Y1 → Y2|r1 → r2
(a)所得が増加すると貨幣需要曲線が右方シフトする。その結果、利子率は上昇する。
(b)所得と利子率だけをプロットしたもの。
Y1 → Y3|r1 → r3
(a)所得が減少すると貨幣需要曲線が左方シフトする。その結果、利子率は下降する。
(b)所得と利子率だけをプロットしたもの。
上記のように、所得水準と利子率の関係をLM曲線に表すと右上がりとなる。
応用問題
1)ケインジアンの交差図のモデルを用いて、以下にあげる変化が均衡GDPに及ぼす影響を予測しなさい。各場合について、変化の方向を述べ、影響の大きさを表す公式を示しなさい。
a 政府購入の増加
b 増税
c 政府購入の増加とそれと同額の増税
a

Gの増加により計画支出が上方シフトし、GDPは増える。増加量は以下となる。
$${ΔY = \frac{1}{1 - MPC}ΔG}$$
b
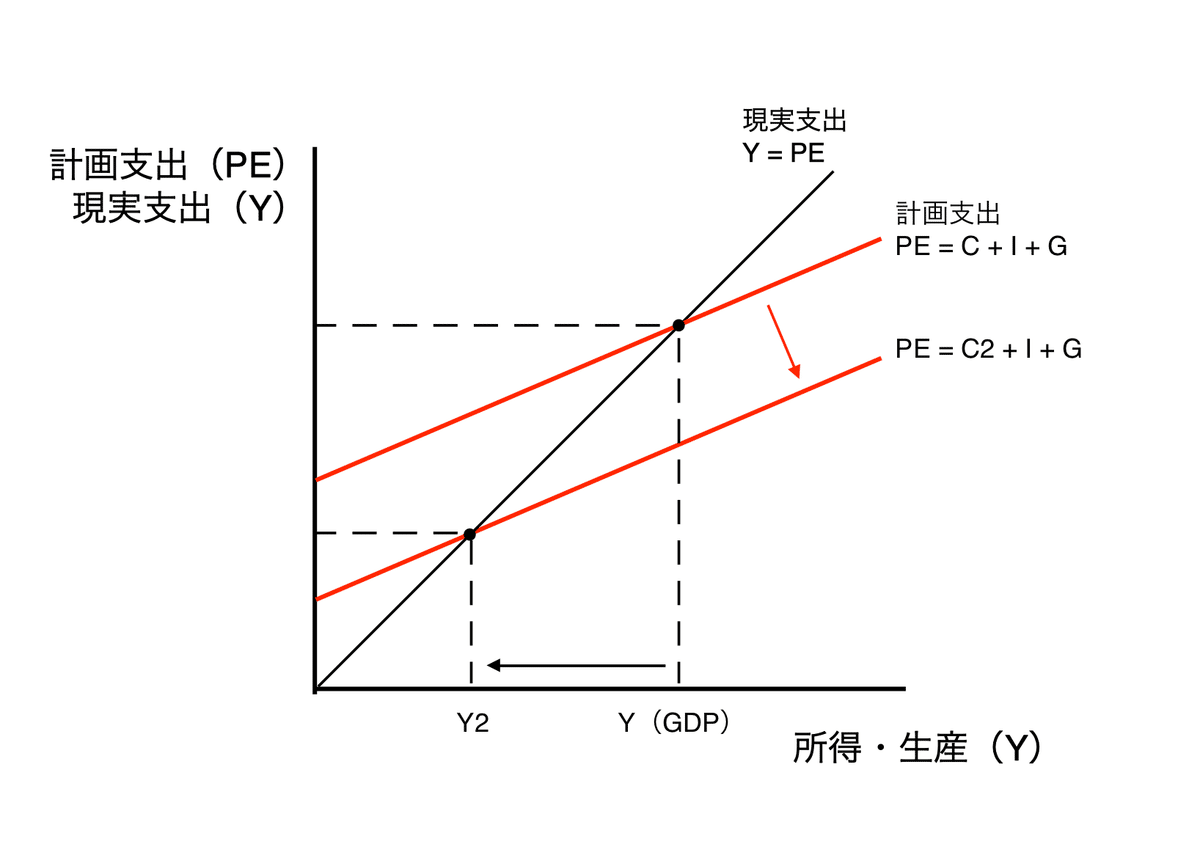
Tの増加によりC(Y - T)が減少、その結果計画支出は下方シフトし、GDPは減る。減少量は以下となる。
$${ΔY = -\frac{MPC}{1 - MPC}ΔT}$$
c
aとbの結果を合わせて考えれば良いため、
$${ΔY = \frac{1}{1 - MPC}ΔG -\frac{MPC}{1 - MPC}ΔT}$$
$${ΔG = ΔT}$$なので、
$${ΔY = \frac{1 - MPC}{1 - MPC}ΔG = ΔG}$$
GDPは$${ΔG}$$増える。
2)ケインジアンの交差図のモデルにおいて、消費関数が、
C = 120 + 0.8 (Y - T)
で与えられるとする。計画投資は200であり、政府購入と租税はともに400である。
a 計画支出を所得の関数としてグラフに描きなさい。
b 均衡所得水準を求めなさい。
c 政府購入が420に増加したときの新しい均衡所得を求めなさい。政府購入の乗数はいくらか。
d 2400の所得を達成するためには、どれだけの政府購入の水準が必要か。(租税は400のままであるとする。)
e 2400の所得を達成するためには、どれだけの租税が必要とされるか。(政府購入は400のままであるとする。)
a
PE = C + I + G = 120 + 0.8 (Y - 400) + 200 + 400 = 0.8Y + 400
Y = PE と PE = 0.8Y + 400 を解くと、Y = 2000
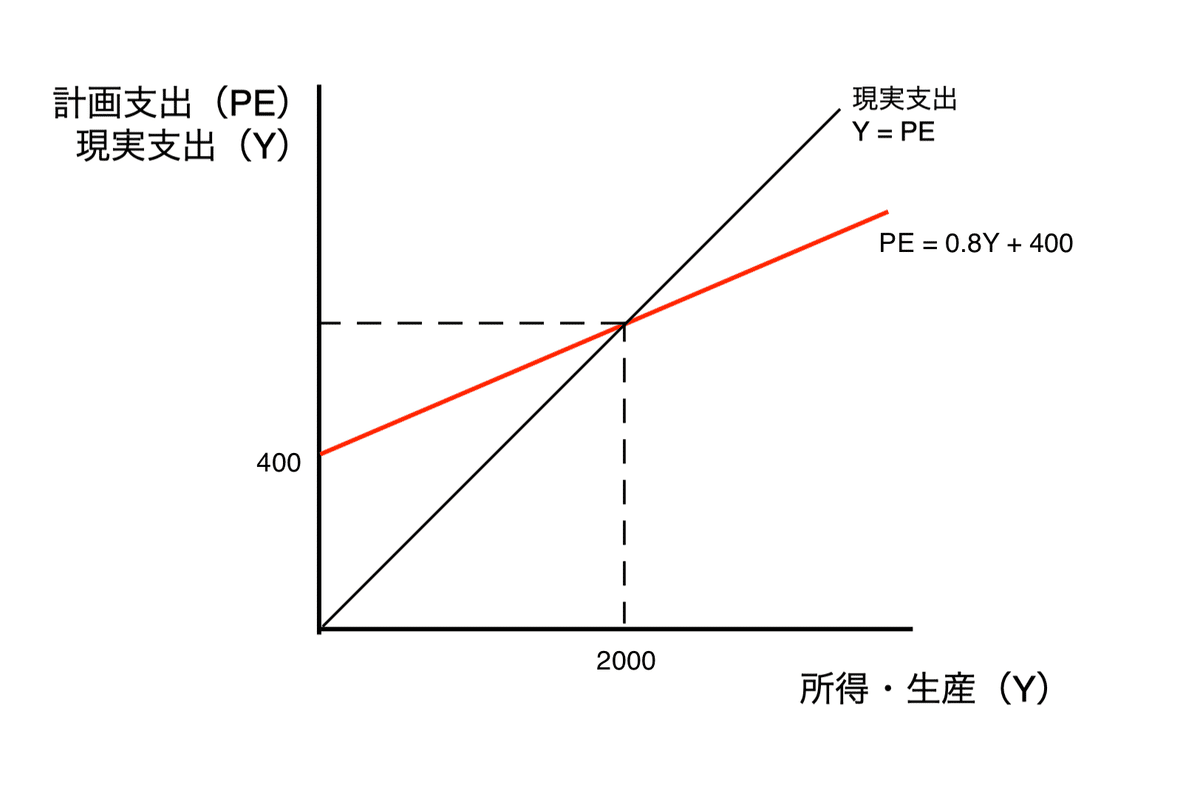
b
2000(aのグラフを描くときに求めてしまったのでaを参照)
c
均衡所得
PE = C + I + G = 120 + 0.8 (Y - 400) + 200 + 420 = 0.8Y + 420
Y = 0.8Y + 420 より、Y = 2100
政府購入乗数
(2100 - 2000)/(420 - 400)= 5
d
(2400 - 2000)/ 5 = 80 より、
G = 480(80の追加購入が必要)
e
$${\frac{ΔY}{ΔG} = \frac{1}{1 - MPC} = 5}$$なので、
$${MPC = 0.8}$$
したがって、租税乗数は
$${\frac{ΔY}{ΔT} = -\frac{MPC}{1 - MPC} = -\frac{0.8}{1 - 0.8} = -4}$$
(2400 - 2000)/ -4 = -100 より、
T = 300(100の減税が必要)
3)本章におけるケインジアンの交差図の説明では、税額を一定と仮定していた。しかし、たいていの国で課されている租税のなかには国民所得とともに自動的に上昇するものがある。(アメリカの例では所得税および給与税がそのなかに含まれる。)租税体系を表す税収の式が次のように書けるとしよう。
$${T = \bar{T} + tY}$$
ここで、$${\bar{T}}$$とtは税制を表すパラメーターであり、tは限界税率である。すなわち、所得が1ドル増加したとき、租税はt×1ドル増加する。
a この税体系は、GDPの変化に対する消費の反応をどのように変えるか。
b ケインジアンの交差図において、この税体系は政府購入乗数をどのように変えるか。
c IS-LMモデルにおいて、この税体系はIS曲線の傾きをどのように変えるか。
a
$${C = C(Y - T)}$$に$${T = \bar{T} + tY}$$を代入すると、$${C = C((1-t)Y - \bar{T})}$$となり、GDP1単位の増加に対する消費の反応は1から1 - tへと減少する。
b
政府購入1単位の増加に対する所得の増加も1-tになるため、政府購入乗数は
$${\frac{ΔY}{ΔG} = \frac{1}{1 - (1 - t)MPC}}$$
となる。
c
イメージがつかなかったため、任意の数値を入れて試してみたところ下図のような結果が得られた。

(右)MPCを固定して税率tを変動させてみる操作
1/1-MPCは租税体系が存在しない通常のモデル
1/1-(1-t)MPCは租税体系が反映されたモデル
この点については直感通りではあるが、政府購入乗数は税体系を考慮しなかったときよりも下がる(そして税率が低いほど乗数への影響が小さくなっていく)ことがわかる。また、MPCが高いほど、税体系を考慮しなかった場合と税体系を考慮した場合の齟齬が大きくなっていくことがわかる。
IS曲線への影響としては、tが大きくなるほど曲線が変化しにくく(急に)、tが小さくなるほど曲線が変化しやすく(緩やかに)なることが予想される(税体系の話なのでtについてのみ記述)。
4)ケインジアンの交差図のモデルにおいて、節約の増加の影響を考えよう。消費関数が、
$${C = \bar{C} + c(Y - T)}$$
であると想定する。ここで、$${\bar{C}}$$は自発的消費と呼ばれるパラメーターであり、消費への外生的な影響を表す。cは限界消費性向である。
a 社会がより節約的になることが$${\bar{C}}$$の減少で表されるとすると、そのとき均衡所得はどうなるか。
b 均衡貯蓄はどうなるか。
c この結果は節約のパラドックスと呼ばれる。その理由は何だとあなたは考えるか。
d このパラドックスは第3章の古典派モデルでも生じるか。それとも生じないか。その理由は何か。
a

$${\bar{C}}$$の減少により結果計画支出は下方シフトし、均衡所得は減る。
b
乗数効果によりΔC < ΔYとなる。
S = Y - C - Gであり、ΔC < ΔYのため、Sは減少する。
c
社会がより節約的になることで、社会の所得が減少してしまっているから。
節約のパラドックス:
自律的貯蓄の増加が総需要(総生産)の減少につながり、総貯蓄が減少すること。狭義には、個人が貯蓄を増やそうとすると総貯蓄が減少する可能性があること。合成の誤謬の一例として知られる。
d
第3章では、以下のような仮定を置いていた。
$${\bar{Y} - C(\bar{Y} - \bar{T}) - \bar{G} = I(r) = \bar{S}}$$
この前提において社会がより節約的になる(Cが減少する)と、Sは増加する関係にある(Yも固定されているため所得の減少が起こらない)。
したがって、第3章の古典派モデルでは節約のパラドックスは発生しない。
5)貨幣需要関数が、
$${(\frac{M}{P})^d = 800 - 50r}$$
であるとしよう。ここで、rはパーセントで表した利子率である。マネーサプライMは2000であり、物価水準Pは5である。
a 実質貨幣残高の需要と供給のグラフを描きなさい。
b 均衡利子率を求めなさい。
c マネーサプライが2000から1500に減少すると、均衡利子率はどうなるか。
d 中央銀行が利子率を4%にしたい場合、マネーサプライをいくらにすべきか。
a
$${(\frac{M}{P})^d = \frac{M}{P}}$$となるのは、
$${\frac{M}{P} = \frac{2000}{5} = 400 = 800 - 50r}$$のときであり、
r = 8で均衡する。

b
8(aのグラフを描くときに求めてしまったのでaを参照)
c
$${\frac{M}{P} = \frac{1500}{5} = 300 = 800 - 50r}$$
r = 10
d
$${\frac{M}{P} = \frac{M}{5} = 800 - 50r = 600}$$
M = 3000
6)ある経済が次のような方程式で表されるものとする。
Y = C + I + G
C = 50 + 0.75(Y - T)
I = 150 - 10r
$${(\frac{M}{P})^d = Y - 50r}$$
G = 250
T = 200
M = 3000
P = 4
a 各変数が何であるかを明らかにし、その意味を簡単に説明しなさい。
b 上の方程式のなかで関連のある方程式を用いてIS曲線を導出しなさい。適切な記号を付けたグラフ上にIS曲線を描きなさい。
c 上の方程式のなかで関連のある方程式を用いてLM曲線を導出しなさい。問bで用いた同一のグラフ上にLM曲線を描きなさい。
d 均衡所得水準と均衡利子率を求めなさい。
a
Y:総生産
C:消費
I:投資
G:政府購入
T:税収
r:利子率
M:マネーサプライ
P:物価水準
$${(\frac{M}{P})}$$:実質貨幣残高
$${(\frac{M}{P})^d}$$:実質貨幣残高需要
Y = C + I + G
閉鎖経済においてGDPの構成要素を支出に分解した国民所得勘定の恒等式。
C = 50 + 0.75(Y - T)
消費が「自発的消費(50)」と「MPC(0.75)」と「可処分所得(Y - T)」によって決まることを表す関数。
I = 150 - 10r
投資が利子率に依存することを表す関数。
$${(\frac{M}{P})^d = Y - 50r}$$
流動性選好理論を適用し、実質貨幣残高需要を利子率に対して負・所得に対して正の関係を持つものとして描いた貨幣需要関数。
b
(計算の都合上、dまで終わってからグラフを描画します)
$${Y = C + I + G = 50 + 0.75(Y - 200) + 150 - 10r + 250}$$
$${= 300 + 0.75Y - 10r}$$
$${Y = 1200 - 40r}$$
c
$${(\frac{M}{P})^d = \frac{M}{P} = \frac{3000}{4} = Y - 50r}$$
$${Y = 750 + 50r}$$
d
bとcより、
1200 - 40r = 750 + 50r
r = 5(均衡利子率)
Y = 1000(均衡所得水準)

第十章 総需要Ⅱ:IS-LMモデルの応用
復習問題
1)なぜ総需要曲線は右下がりなのか説明しなさい。
まず、物価水準が変化するとIS-LMモデルに何が起こるのかを調べる。仮に物価水準がP1からP2に上昇した場合、LM曲線は以下の図のようにシフトする(実質貨幣残高が左方シフトし、利子率が上昇する。その結果、所与の所得YにおけるLM曲線は上方シフトする。)。

LM曲線の上方シフトは、IS-LMモデルにおける均衡所得に下図のような影響を与える(均衡所得がY1からY2に下降する)。
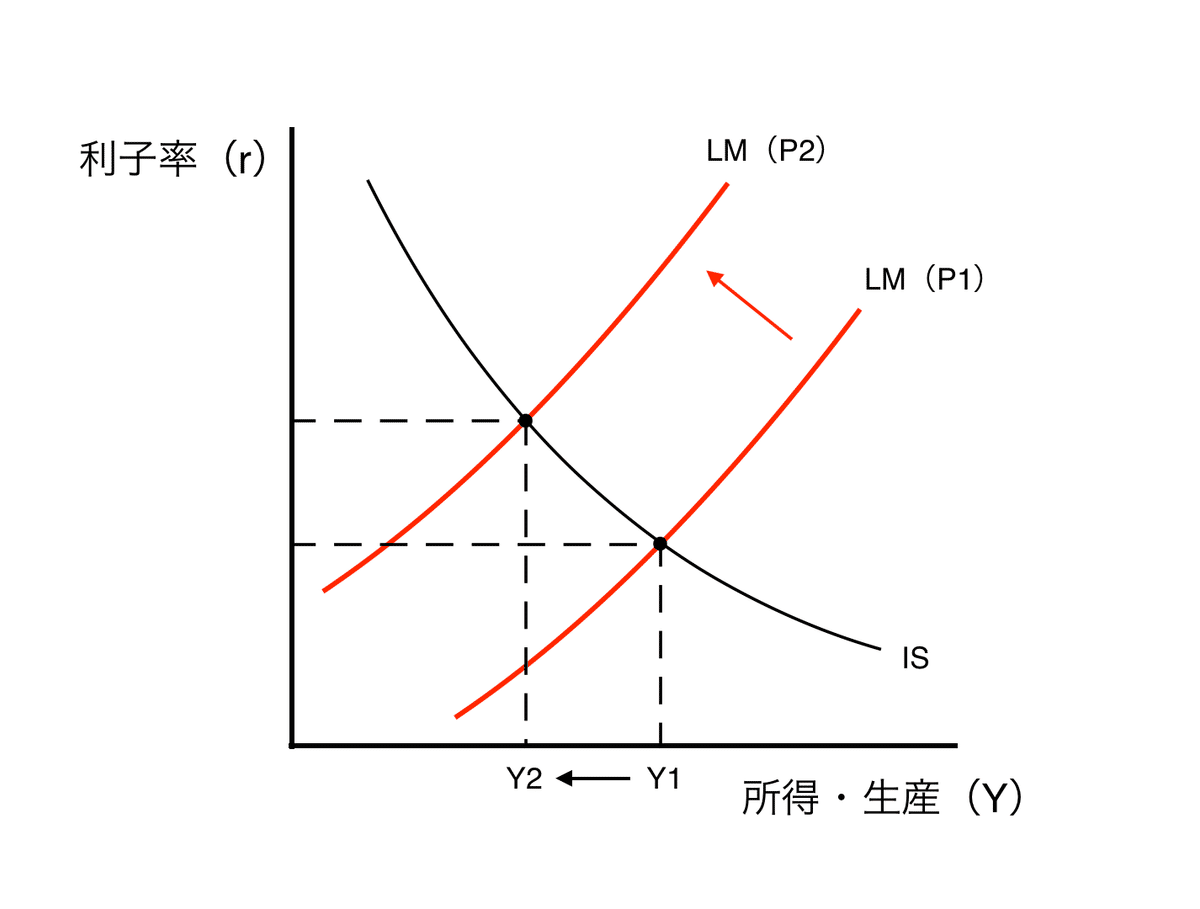
総需要曲線は、物価水準と所得の関係をまとめたものであった。物価水準のP1からP2への上昇と、所得Y1からY2への下降が対応しており、下図のように表現される。逆に、物価水準が下降する際は所得が上昇する。これらのPとYの対応関係を出力すると、総需要曲線は右下がりになる。
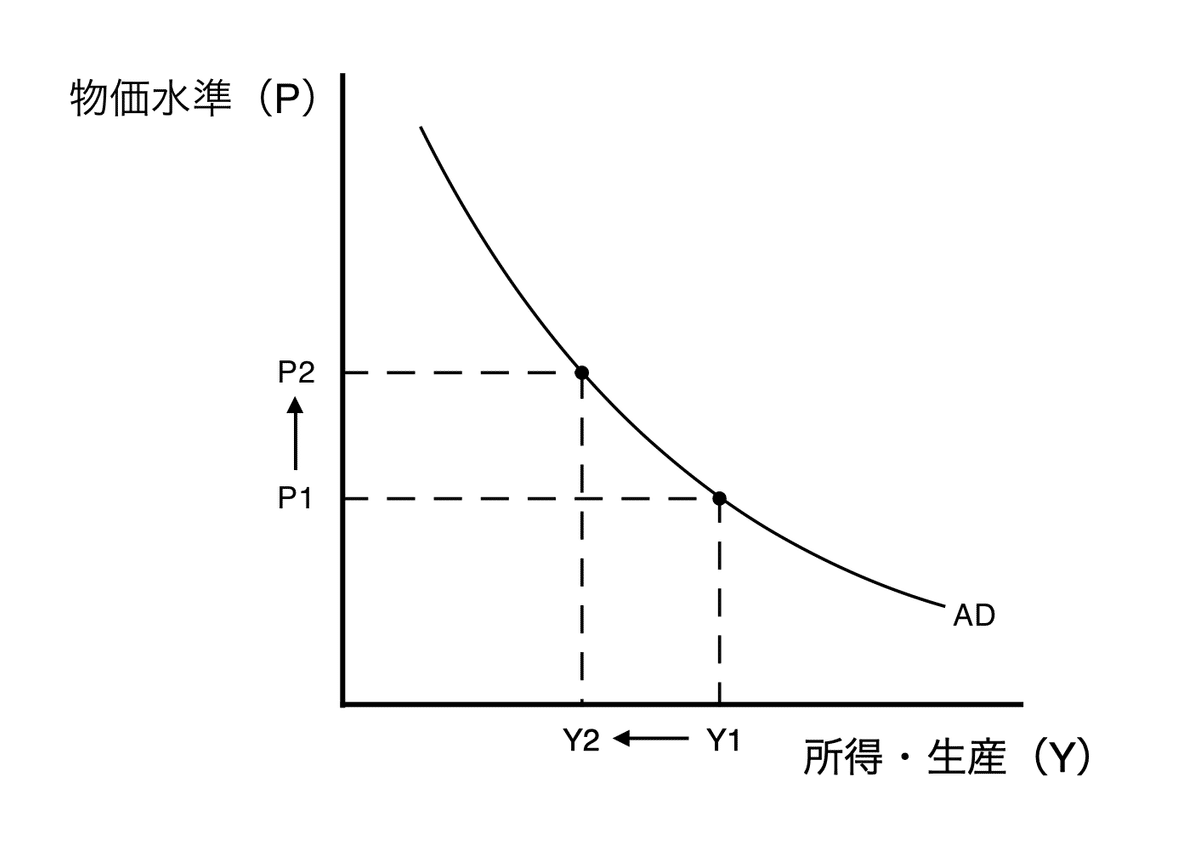
2)増税が利子率、所得、消費、投資に与える影響はどのようなものか。
租税乗数は$${\frac{ΔY}{ΔT} = -\frac{MPC}{1 - MPC}}$$であり、増税はIS曲線を$${ΔT * (-\frac{MPC}{1 - MPC})}$$(①)シフトさせる。

利子率
r1からr2に下がる。
所得
Y1からY2に下がる。
消費
C = C(Y - T)においてTが増えYが減るとCも減る。
投資
I = I(r)であり、rが下がるとIは上がる。
ただし、利子率の減少が投資を促進するため、IS-LMモデルにおける所得の減少はケインジアンの交差図よりも小さくなる。
3)マネーサプライの減少が利子率、所得、消費、投資に与える影響はどのようなものか。
マネーサプライの減少はLM曲線を上方シフトさせる。

利子率
r1からr2に上がる。
所得
Y1からY2に下がる。
消費
C = C(Y - T)においてYが減るとCも減る。
投資
I = I(r)であり、rが上がるとIは下がる。
4)物価下落が均衡所得に与える影響について、考えられるものを述べなさい。
<所得の増加(IS-LMモデル)>
物価水準の下落は実質貨幣残高M/Pの増加を意味する。実質貨幣残高の増加はLM曲線の下方シフトを引き起こし、所得の増加をもたらす。
<所得の増加(ピグー効果)>
古典派経済学者アーサー・ピグーは、実質貨幣残高は家系の富の一部であると指摘した。物価水準が下落して実質貨幣残高が増加すると、消費者は豊かさが増したと感じるようになり、支出を増やす。この消費者支出の増加はIS曲線の上方シフトを引き起こし、所得の増加をもたらす。
<所得の減少(負債(デット)デフレーション理論)>
予想外のデフレーションの影響。予想外のデフレーションは債権者を豊かにし、債務者を貧しくする(実質貨幣価値が変わるから)。債務者は債権者よりも支出性向が高いため、債権者が支出を増やす以上に債務者は支出を減らす。それらを差し引きした結果、支出は減少し、IS曲線は下方シフトし、所得の減少をもたらす。
<所得の減少(IS-LMモデルの拡張)>
予想されるデフレーションの影響。期待デフレーションはどのような所与の名目利子率に対しても実質利子率を上昇させ(r = i - πであり、πが負になればrは上昇する)、投資支出が減少する。投資の減少はIS曲線を下方シフトさせ、所得の減少をもたらす。
応用問題
1)IS-LMモデルによれば、次のような場合に短期の利子率、所得、消費、投資はどうなるか。解答には必ず適切なグラフを付け加えなさい。
a 中央銀行がマネーサプライを増やす。
b 政府が政府購入を増やす。
c 政府が増税する。
d 政府が政府購入と租税を同額増やす。
a
マネーサプライの増加は、LM曲線を下方シフトさせる。

利子率
r1からr2に下がる。
所得
Y1からY2に上がる。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、rが下がるとIは上がる。
b
政府購入の増加は、IS曲線を上方シフトさせる。

利子率
r1からr2に上がる。
所得
Y1からY2に上がる。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、rが上がるとIは下がる。
c
増税は、IS曲線を下方シフトさせる。

利子率
r1からr2に下がる。
所得
Y1からY2に下がる。
消費
C = C(Y - T)においてYが減りTが増えるとCは減る。
投資
I = I(r)であり、rが下がるとIは上がる。
d
政府購入乗数は、$${\frac{ΔY}{ΔG} = \frac{1}{1 - MPC}}$$
租税乗数は、$${\frac{ΔY}{ΔT} = -\frac{MPC}{1 - MPC}}$$であり、
$${ΔY = (\frac{1}{1 - MPC})ΔG - (\frac{MPC}{1 - MPC})ΔT}$$である。
ここで、ΔG = ΔTであるから、
$${ΔY = (\frac{1}{1 - MPC})ΔG - (\frac{MPC}{1 - MPC})ΔG = (\frac{1 - MPC}{1 - MPC})ΔG = ΔG}$$
したがって、IS曲線がΔG分右方シフトする。

利子率
r1からr2に上がる。
所得
Y1からY2に上がる。
消費
C = C(Y - T)においてYもTも増える。ここで、Y2 - Y1とΔTを比較すると、(Y2 - Y1 = ΔG = ΔT)であるから、ΔTの方が大きい。ゆえに消費は減る。
投資
I = I(r)であり、rが上がるとIは下がる。
2)IS-LMモデルを用いて、下記のショックそれぞれが所得、利子率、消費、投資に与える影響を予測しなさい。それぞれの場合において、所得を当初の水準に維持するために中央銀行は何をすべきかを説明しなさい。それぞれの解答には必ずグラフを用いなさい。
a 新しい高速コンピュータ半導体素子が発明されて、多くの企業がコンピュータ・システムを新しいものと取り替える。
b クレジットカード詐欺の急増によって、人々が現金で取引する回数を増やす。
c 『裕福な老後』というタイトルの本がベストセラーになり、その影響で人々が所得に占める貯蓄の割合を高めようと考える。
d 新しいハト派の連邦準備議長の任命によって期待インフレ率が上昇する。
a
投資需要の増加はIS曲線を上方シフトさせる。

所得
Y1からY2に上がる。
利子率
r1からr2に上がる。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、投資需要の増加は利子率の上昇によって若干相殺されるが、全体としては投資は増えると予想される。
中央銀行が所得を当初の水準に維持するためには、マネーサプライを減少させることでLM曲線に上方圧力を加える必要がある(金利はさらに上がる)。
b
Yが固定されている状態での貨幣需要の増加は利子率の上昇をもたらし、LM曲線を上方シフトさせる。

所得
Y1からY2に下がる。
利子率
r1からr2に上がる。
消費
C = C(Y - T)においてYが減るとCも減る。
投資
I = I(r)であり、rが上がるとIは下がる。
中央銀行が所得を当初の水準に維持するためには、マネーサプライを増加させることでLM曲線に下方圧力を加える必要がある(ショックの影響は相殺される)。
c
消費の低下はIS曲線を下方シフトさせる。

所得
Y1からY2に下がる。
利子率
r1からr2に下がる。
消費
C = C(Y - T)においてYが減るとCは減る(限界消費性向も下がりそうなのでさらに減る)。
投資
I = I(r)であり、rが下がるとIは上がる(民間貯蓄からの投資は若干下がりそう)。
中央銀行が所得を当初の水準に維持するためには、マネーサプライを増加させることでLM曲線に下方圧力を加える必要がある(金利はさらに下がる)。
d
名目利子率iと期待インフレ率Eπを分けて考えることとする。期待インフレ率はIS曲線の変数に含まれ、期待インフレ率が上昇すると、IS曲線は上方シフトする。

所得
Y1からY2に上がる。
利子率
名目利子率はi2に、実質利子率はr2に上がる。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、rが上がるとIは下がる。
中央銀行が所得を当初の水準に維持するためには、マネーサプライを減少させることでLM曲線に上方圧力を加える必要がある(名目金利が実質金利に追いつく)。
3)ヒクソニア(Hicksonia)という国の経済を考える。
a 消費関数は、
C = 300 + 0.6(Y - T)
投資関数は、
I = 700 - 80r
で与えられる。政府購入と租税はともに500である。この経済について、0 ≦ r ≦ 8 におけるIS曲線のグラフを描きなさい。
b ヒクソニア国の貨幣需要関数は、
$${(\frac{M}{P})^d = Y - 200r}$$
である。マネーサプライMは3000であり、物価水準Pは3である。この経済について、0 ≦ r ≦ 8 におけるLM曲線のグラフを描きなさい。
c 均衡利子率rと均衡所得水準Yを求めなさい。
d 政府購入が500から700に増加したとしよう。IS曲線はどのようにシフトするか。新しい均衡利子率と均衡所得水準はどうなるか。
e 政府購入は100のままとして、マネーサプライが3000から4500に増加したとしよう。LM曲線はどのようにシフトするか。新しい均衡利子率と均衡所得水準はどうなるか。
f 金融政策と財政政策は初期値のままで、物価水準が3から5に上昇したとしよう。どんなことが起こるか。新しい均衡利子率と均衡所得水準はどうなるか。
g 金融政策と財政政策の初期の値に対して総需要曲線の方程式を導出し、グラフを描きなさい。財政政策や金融政策が問dとeのように変化したとき、この総需要曲線はどのようになるか。
a
Y = C + I + Gに与式を代入すると、
Y = 300 + 0.6(Y - 500) + 700 - 80r + 500
Y = 3000 - 200r

b
$${\frac{M}{P} = \frac{3000}{3} = Y - 200r}$$
Y = 1000 + 200r

c
3000 - 200r = 1000 + 200rを解くと、
r = 5
Y = 2000

d
Y = 300 + 0.6(Y - 500) + 700 - 80r + 700
Y = 3500 - 200r
3500 - 200r = 1000 + 200rを解くと、
r = 6.25
Y = 2250

e
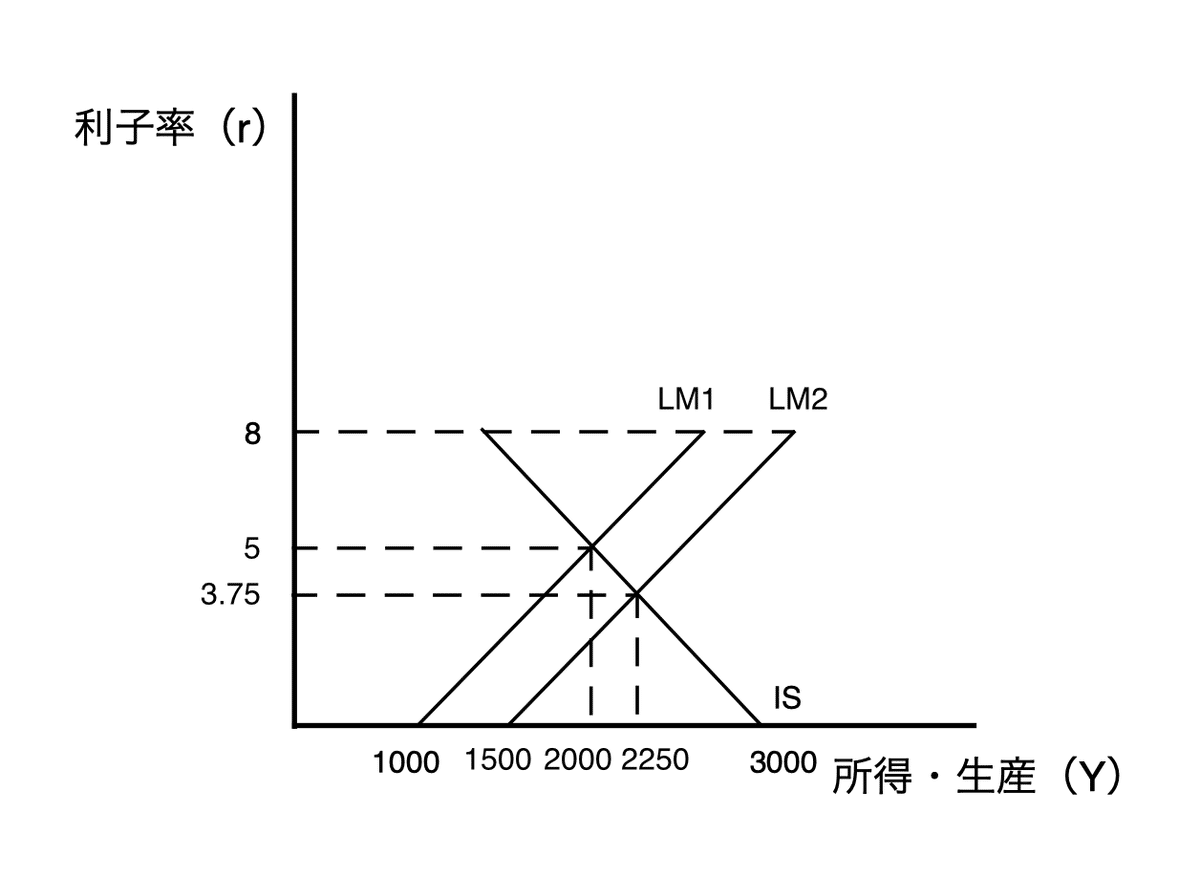
私の持っている版だと「政府購入は100のままとして」と書いてあるのですが、「ままとして」を尊重して誤植と見なし、政府購入を500のままとして解きます。
$${\frac{M}{P} = \frac{4500}{3} = Y - 200r}$$
Y = 1500 + 200r
3000 - 200r = 1500 + 200rを解くと、
r = 3.75
Y = 2250
f
$${\frac{M}{P} = \frac{3000}{5} = Y - 200r}$$
Y = 600 + 200r
3000 - 200r = 600 + 200rを解くと、
r = 6
Y = 1800

g
総需要曲線の方程式とは、PとYの関係であった。
$${Y = 3000 - 200r、\frac{3000}{P} = Y - 200r}$$をYとPの関係式として整理すると、
$${Y = 1500 + \frac{1500}{P}}$$

dの場合、
$${Y = 3500 - 200r、\frac{3000}{P} = Y - 200r}$$から、
$${Y = 1750 + \frac{1500}{P}}$$

eの場合、
$${Y = 3000 - 200r、\frac{4500}{P} = Y - 200r}$$から、
$${Y = 1500 + \frac{2250}{P}}$$

4)初期の経済が以下の方程式で表されるものとする。
C = 500 + 0.75(Y - T)
I = 1000 - 50r
$${\frac{M}{P} = Y - 200r}$$
G = 1000
T = 1000
M = 6000
P = 2
a IS曲線とLM曲線を導出し、そのグラフを描きなさい。
b 新しく選ばれた大統領が20%の減税を行った。貨幣供給は一定に維持されると仮定すると、新しい均衡利子率と均衡所得水準はどうなるか。租税乗数はいくらか。
c ここで中央銀行が利子率を一定に保つように貨幣供給を調整すると仮定する。新しい所得水準はいくらか。新しい貨幣供給はいくらでなければならないか。租税乗数はいくらか。
d ここで中央銀行が所得水準を一定に保つように貨幣供給を調整すると仮定する。新しい均衡利子率はいくらか。貨幣供給はいくらでなければならないか。租税乗数はいくらか。
e 問b、c、dで計算した均衡を問aで描いたグラフの上に示しなさい。
a
IS曲線は、Y = C + I + Gに与式を代入し、
Y = 500 + 0.75(Y - 1000) + 1000 - 50r + 1000
Y = 7000 - 200r
LM曲線は、$${\frac{M}{P} = Y - 200r}$$に与式を代入し、
Y = 3000 + 200r
7000 - 200r = 3000 + 200rを解くと、
r = 10
Y = 5000

b
Y = 500 + 0.75(Y - 800) + 1000 - 50r + 1000
Y = 7600 - 200r
7600 - 200r = 3000 + 200r
r = 11.5
Y = 5300
(5300 - 5000) / (800 - 1000) = -1.5
c
中央銀行は、bで上方シフトしたIS曲線による金利の変化を打ち消すようにマネーサプライを増やし、LM曲線に下方圧力を加える(LM1 → LM2)。

r = 10のとき、Y = 7600 - 200rから、Y = 5600
$${\frac{M}{2} = 5600 - 2000}$$となるため、
M = 7200
(5600 - 5000) / (800 - 1000) = -3
d
中央銀行は、bで上方シフトしたIS曲線による所得の変化を打ち消すようにLM曲線に上方圧力を加える(LM1 → LM2)。

7600 - 200r = 5000から、
r = 13
$${\frac{M}{2} = 5000 - 2600}$$より、
M = 4800
(5000 - 5000) / (800 - 1000) = 0
e

5)以下に述べる事柄の各々が正しいか誤りかを明らかにし、その理由を説明しなさい。正しい場合の各々について、これらの特別なケースにおける金融政策と財政政策の効果について普通とは異なることがなにかあるか論じなさい。
a もし投資が利子率に依存しなければ、LM曲線は水平である。
b もし投資が利子率に依存しなければ、IS曲線は垂直である。
c もし貨幣需要が利子率に依存しなければ、LM曲線は垂直である。
d もし貨幣需要が利子率に依存しなければ、LM曲線は水平である。
e もし貨幣需要が所得に依存しなければ、LM曲線は水平である。
f もし貨幣需要が利子率に対して極端に感応的であれば、LM曲線は水平である。
a
IS曲線は財・サービス市場の均衡を表し(Y = C + I(r) + G)、LM曲線は実質貨幣残高市場の均衡を表した$${(\frac{M}{P})^d = L(r, Y)}$$。投資が利子率に依存しないことはLM曲線に影響しないため、命題は誤り。
b
命題は正しい。(参考)

IS曲線が垂直であるため、マネーサプライの増減による金融政策(LM曲線のシフト)は、生産に影響を与えられなくなり、金利には影響を与えられるままである。政府購入や租税の増減による財政政策(IS曲線のシフト)は、生産にも金利にも影響を与えられるままである。
c
命題は正しい。(参考)

LM曲線が垂直であるため、マネーサプライの増減による金融政策(LM曲線のシフト)は、生産にも金利にも影響を与えられるままである。政府購入や租税の増減による財政政策(IS曲線のシフト)は、生産に影響を与えられなくなり、金利には影響を与えることができるままである。
d
垂直になるため、命題は誤り。
e
$${(\frac{M}{P})^d = L(r)}$$となり、実質貨幣残高市場における貨幣需要はrに対応する形で水平となる。したがって、命題は正しい。

LM曲線が水平であるため、マネーサプライの増減による金融政策(LM曲線のシフト)は、生産にも金利にも影響を与えられるままである。政府購入や租税の増減による財政政策(IS曲線のシフト)は、金利に影響を与えられなくなり、生産には影響を与えることができるままである。
f
流動性の罠を指していると解釈すれば、命題は正しい。(参考)
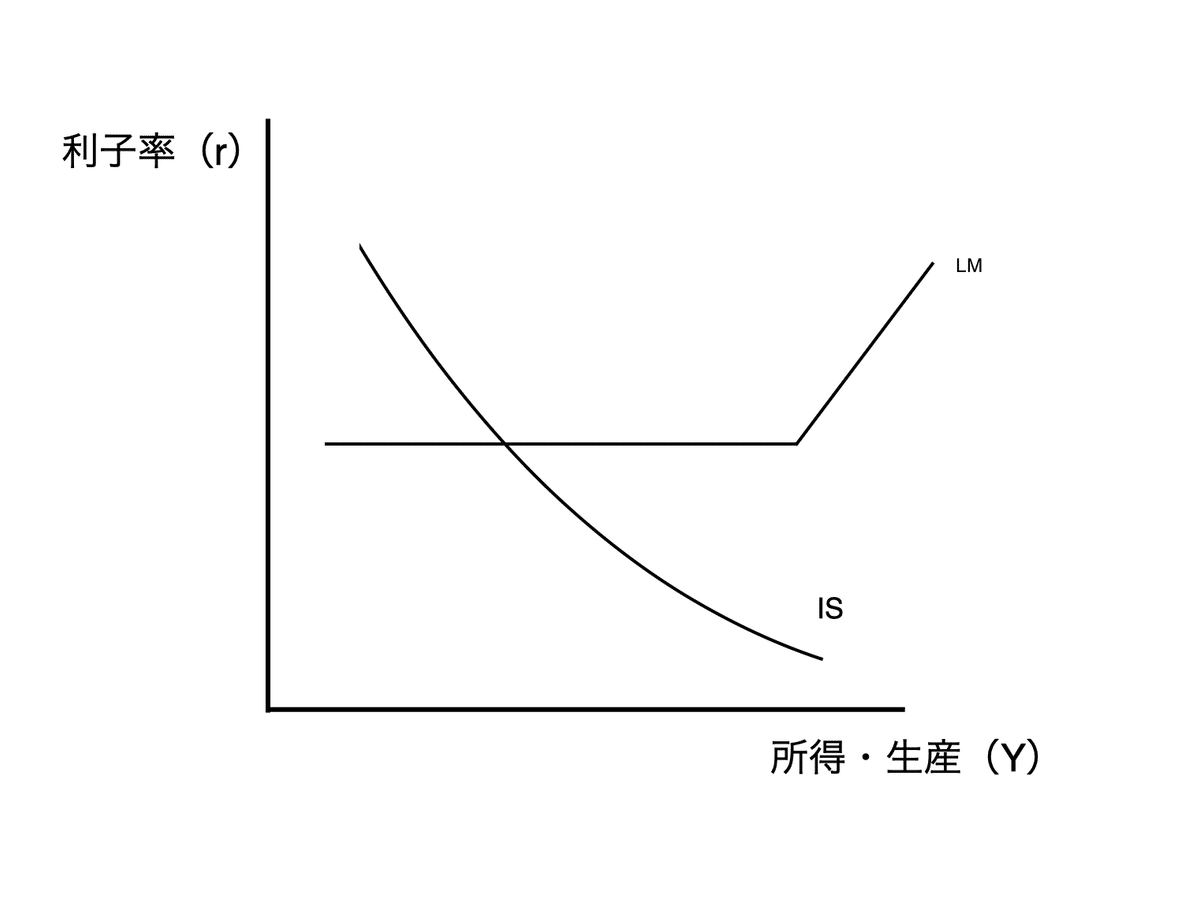
LM曲線が水平であるため、マネーサプライの増減による金融政策(LM曲線のシフト)は、生産にも金利にも影響を与えられるままである。政府購入や租税の増減による財政政策(IS曲線のシフト)は、金利に影響を与えられなくなり、生産には影響を与えることができるままである。(厳密には、最低利子率に到達するまでの間はIS曲線のシフトが有効である点がeと異なる)
6)金融政策と財政政策は多くの場合同時に変化する。
a 投資を増加させたいが、産出量は変化させたくないと政府が考えているとしよう。IS-LMモデルにおいて、金融政策と財政政策をどのように組み合わせればこの目標を達成できるだろうか。
b 1980年代初期に、アメリカ政府は減税を行って財政赤字になったが、連邦準備は緊縮的な金融政策を実施した。このポリシー・ミックスはどのような効果を持つだろうか。
a
利子率が下がり生産が変わらないようにすればよいため、
・金融政策:マネーサプライの増加によりLM曲線に下方圧力
・財政政策:増税・政府購入の減少によりIS曲線に下方圧力
をかければよい。
b
IS-LM曲線においては下図のような解釈となる。

所得の変化は各政策の影響度合いによって変わる。利子率は上昇し、その結果、投資は減少する。消費は、所得の減少が大きすぎない限りは、減税の影響で上昇すると予想される。
7)IS-LMの図を用いて、以下の変化が国民所得、利子率、物価水準、消費、投資、実質貨幣残高に与える影響を短期と長期の両方について述べなさい。
a マネーサプライの増加
b 政府購入の増加
c 増税
本問の前提として、a~cのショックが発生する前は長期均衡水準を満たした状態であることを仮定する。
a

【短期】
国民所得
$${\bar{Y}}$$からY2に増える。
利子率
r1からr2に下がる。
物価水準
短期では物価水準は硬直的であるため変わらない。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、rが下がるとIは上がる。
実質貨幣残高
$${\frac{M}{\bar{P}}}$$においてMが大きくなるため実質貨幣残高も大きくなる。
【長期】
国民所得
自然産出率$${\bar{Y}}$$に収束する。
利子率
r2からr1に戻る。
物価水準
上がる。
消費
所得が減るため元の水準に戻る。
投資
金利が上がるため元の水準に戻る。
実質貨幣残高
物価上昇によって元の水準に戻る。
b
政府購入の増加はIS曲線を上方シフトさせる。

【短期】
国民所得
$${\bar{Y}}$$からY2に増える。
利子率
r1からr2に上がる。
物価水準
短期では物価水準は硬直的であるため変わらない。
消費
C = C(Y - T)においてYが増えるとCも増える。
投資
I = I(r)であり、rが上がるとIは下がる。
実質貨幣残高
変わらない。
【長期】
国民所得
自然産出率$${\bar{Y}}$$に収束する。
利子率
r2からr3に上がる。
物価水準
上がる。
消費(自信ありません)
元の水準に戻る(元の水準よりも少し減る?)。
投資
元の水準よりも下がる。
実質貨幣残高
物価上昇の影響で、元の水準よりも小さくなる。
c
増税はIS曲線を下方シフトさせる。

【短期】
国民所得
$${\bar{Y}}$$からY2に減る。
利子率
r1からr2に下がる。
物価水準
短期では物価水準は硬直的であるため変わらない。
消費
C = C(Y - T)においてYが減りTが増えるとCも減る。
投資
I = I(r)であり、rが下がるとIは上がる。
実質貨幣残高
変わらない。
【長期】
国民所得
自然産出率$${\bar{Y}}$$に収束する。
利子率
r2からr3に下がる。
物価水準
下がる。
消費
元の水準に向かって回復するが、増税分の影響で元の水準には届かない。
投資
さらに利子率がさがるため、より上がる。
実質貨幣残高
物価が下がるため、元の水準よりも大きくなる。
8)中央銀行が以下の2つの代替的な金融政策を考えているとしよう。
・マネーサプライを一定に保つように利子率を調整する。
・利子率を一定に保つようにマネーサプライを調整する。
IS-LMモデルにおいて、以下のような条件の下ではどちらの政策が産出量をより安定化させるか。その解答について説明しなさい。
a 経済に対するあらゆるショックが財・サービスへの需要の外生的変化から起きる場合。
b 経済に対するあらゆるショックが貨幣需要の外生的変化から起きる場合。
下記のような政策方針として整理される。
マネーサプライを一定に保つように利子率を調整する
=LM曲線をシフトさせない
利子率を一定に保つようにマネーサプライを調整する
=LM曲線をシフトさせる
また、IS曲線は財・サービス市場の均衡を表し、LM曲線は実質貨幣残高市場の均衡を表した。
a
財・サービスへのショックはIS曲線をシフトさせる。

上図のように、LM曲線をシフトさせない(=マネーサプライを一定に保つように利子率を調整する)政策の方が産出量を安定させる。
b
貨幣需要へのショックは、LM曲線をシフトさせる。

上図のように、LM曲線をシフトさせる(=利子率を一定に保つようにマネーサプライを調整する)政策の方が産出量を安定させる。
9)実質貨幣残高への需要が可処分所得に依存するとしよう。すなわち、貨幣需要関数は、
$${\frac{M}{P} = L(r, Y - T)}$$
である。IS-LMモデルを用いて、貨幣需要関数がこのように変更されると以下のことが変わるかどうか論じなさい。
a 政府購入の変化の分析
b 租税の変化の分析
題意の貨幣需要関数の変更はLM曲線だけに影響する。
a
政府購入の変化は、IS曲線をシフトさせるがLM曲線には影響しない(分析も変化しない)。
b
実質貨幣残高需要を考える際に可処分所得を考慮しない通常のIS-LMモデルにおいては、租税の変化はIS曲線だけをシフトさせた。しかし、可処分所得を考慮するモデルでは、租税の変化はLM曲線をも変化させることとなる(下図)。これは、分析結果に大きな変化をもたらす。

10)この問題はIS-LMモデルを代数的に分析するよう求めたものである。消費は可処分所得の1次関数であると仮定する。
C(Y - T) = a+b(Y - T)
ここで、a > 0 および 0 < b < 1 である。パラメーターbは限界消費性向であり、パラメーターaは自発的消費と呼ばれる定数である。また、投資関数も利子率の1次関数であると仮定する。
I(r) = c - dr
ここで、c > 0 および d > 0 である。パラメーターdは利子率に対する投資の感応性の尺度であり、パラメーターcは自発的投資と呼ばれる定数である。
a Yをrと外生変数G,Tおよびモデルのパラメーターa,b,c,dの関数として解きなさい。
b IS曲線の傾きは、投資の利子率に対する感応性を表すパラメーターdにどのように依存するか。問aに対する解答をもとに、言葉で説明しなさい。
c 100ドルの減税と100ドルの政府支出の増加では、どちらがIS曲線を水平方向により大きくシフトさせるか。問aに対する解答をもとに、言葉で説明しなさい。
次に、実質貨幣残高の需要が所得と利子率についての1次関数であると仮定する。
L(r, Y) = eY - fr
ここで、e > 0 および f > 0 である。パラメーターeは貨幣需要の所得に対する感応度の尺度であり、パラメーターfは貨幣需要の利子率に対する感応度の尺度である。
d rをY,M,Pおよびパラメーターe,fの関数として解きなさい。
e 問dに対する解答を用いて、LM曲線の傾きがより急になるのは、fの値が大きい場合か小さい場合かを明らかにし、それを言葉で説明しなさい。
f Mの100ドルの増加から生じるLM曲線のシフトの大きさは、以下の要因にどのように依存するか。
ⅰ 貨幣需要の所得感応度を表すパラメーターeの値
ⅱ 貨幣需要の利子感応度を表すパラメーターfの値
g 問aとdに対する解答を用いて、総需要曲線の式を導出しなさい。ただし、YをPと外生的政策変数M,G,Tおよびモデルのパラメーターの関数として示し、rを含めてはならない。
h 問gに対する解答を用いて、総需要曲線が負の傾きをもつことを証明しなさい。
i 問gに対する解答を用いて、GとMの増加、Tの減少が総需要曲線を右方にシフトさせることを証明しなさい。貨幣需要の利子感応性を表すパラメーターfがゼロのとき、この結果はどのように変わるか。その結果を言葉で説明しなさい。
a
Y = C + I + G = a + b(Y - T) + c - dr + G
(1 - b)Y = a - bT + c - dr + G
$${Y = \frac{a - bT + c - dr + G}{1 - b}}$$
b
dが大きければ大きいほど、投資の利子に対する感応度が上がっていくため、IS曲線は水平に近づいていく。(参考)
c
$${Y = \frac{a - bT + c - dr + G}{1 - b}}$$において、0 < b < 1であることから、同額あたりのYへの影響は政府支出の変更の方が大きい。政府支出の増加は、IS曲線を水平方向により大きくシフトさせる。
d
$${\frac{M}{P} = L(r, Y) = eY - fr}$$
$${fr = eY - \frac{M}{P}}$$
$${r = \frac{eY - \frac{M}{P}}{f}}$$
e
上式より、fが小さい方がLM曲線の傾きは急になる(分母がfであるため)。
f(参考)
ⅰ
貨幣需要の所得感応度が大きくなればなるほど、マネーサプライの増減による影響は小さく(LM曲線の傾きは急に)なる。
ⅱ
貨幣需要の利子感応度が小さくなればなるほど、マネーサプライの増減による影響は小さく(LM曲線の傾きは急に)なる。(これは問eでも議論した)
g
rを消すように指示されているため、
$${Y = \frac{a - bT + c - dr + G}{1 - b}}$$のrに$${r = \frac{eY - \frac{M}{P}}{f}}$$を代入すると、
$${Y = \frac{a - bT + c - d\frac{eY - \frac{M}{P}}{f} + G}{1 - b} = \frac{f(a - bT + c + G) - d(eY - \frac{M}{P})}{f(1 - b)} = \frac{f(a - bT + c + G) - deY + d(\frac{M}{P})}{f(1 - b)}}$$
$${(1 + \frac{de}{f(1 - b)})Y = \frac{f(a - bT + c + G) + d(\frac{M}{P})}{f(1 - b)}}$$
$${Y = \frac{f(a - bT + c + G) + d(\frac{M}{P})}{f(1 - b)}*\frac{f(1 - b)}{f(1 - b) + de} = \frac{f(a - bT + c + G) + d(\frac{M}{P})}{f(1 - b) + de}}$$
h
総需要曲線は、価格と生産量の関係を表すグラフであった。
問gの式において、Pが上昇すると$${\frac{M}{P}}$$は小さくなり($${eY - \frac{M}{P}}$$が大きくなるため$${ - d(eY - \frac{M}{P})}$$も大きくなる)、Yは下降する。Pが下降するとYは上昇する。このことから、総需要曲線が負の傾きを持つことがわかる。
i
Mの増加は、$${d(\frac{M}{P})}$$が大きくなるため、右方シフトに寄与する。Gの増加については式より自明。Tの減少は、-b(T - ΔT) = +bΔTなので、右方シフトに寄与する。
fが0のとき、$${Y = \frac{M}{eP}}$$となり、貨幣需要曲線は「貨幣需要の所得感応度e」、マネーサプライ、物価水準のみによって決定される(貨幣需要の利子感応度が0の場合、LM曲線は垂直になる。この状況については応用問題5のcで図とともに検討した)。
第十一章 開放経済再訪:マンデル=フレミング・モデルと為替相場制度
復習問題
1)変動相場制下のマンデル=フレミング・モデルにおいて、増税が行われたとき、総所得、為替レート、貿易収支に何が生じるかを説明しなさい。変動相場制ではなく固定相場制の場合にはどうか。
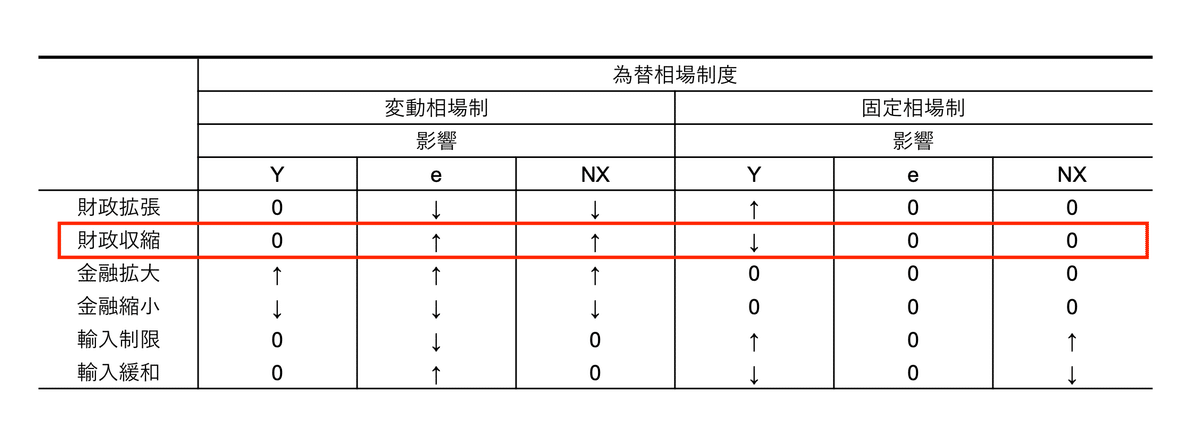
【変動相場制】
増税はIS*曲線を上方シフトさせる。

総所得
変わらない。
為替レート
e1からe2に上昇(減価)する。
貿易収支
NX(e)は、為替レートの上昇により増大する。
【固定相場制】
増税はIS*曲線を上方シフトさせ、LM*曲線を為替レートを保持できるようシフトさせる。

総所得
Y1からY2に減る。
為替レート
変わらない。
貿易収支
変わらない。
2)変動相場制下のマンデル=フレミング・モデルにおいて、マネーサプライが減少したとき、総所得、為替レート、貿易収支に何が生じるかを説明しなさい。変動相場制ではなく固定相場制の場合にはどうか。

【変動相場制】
マネーサプライの減少は、LM*曲線を左方シフトさせる。

総所得
Y1からY2に減る。
為替レート
e1からe2に下降(増価)する。
貿易収支
NX(e)は、為替レートの下降により減少する。
【固定相場制】
LM*曲線は一時的に左方シフトするが、為替レートを一定に保つために中央銀行は自国通貨を売る(=マネーサプライを増加させる)必要が生じ、元の位置に戻る。

総所得
変わらない。
為替レート
変わらない。
貿易収支
変わらない。
3)変動相場制下のマンデル=フレミング・モデルにおいて、輸入車に対する数量割当が撤廃されたとき、総所得、為替レート、貿易収支に何が生じるかを説明しなさい。変動相場制ではなく固定相場制の場合にはどうか。

【変動相場制】
数量割当の撤廃は、IS*曲線を上方シフトさせる。

総所得
変わらない。
為替レート
e1からe2に上昇(減価)する。
貿易収支
為替レートの上昇による増大と数量割当の撤廃による減少が相殺し、変化しない。
【固定相場制】
数量割当の撤廃はIS*曲線を上方シフトさせ、LM*曲線を為替レートを保持できるようシフトさせる。

総所得
Y1からY2に減る。
為替レート
変わらない。
貿易収支
数量割当の撤廃により減少する。
4)変動相場制と固定相場制の優れている点をそれぞれあげなさい。
マンデル=フレミング・モデルでは、金融政策と財政政策が総所得に与える影響は為替相場制度に依存している。変動相場制では、金融政策だけが所得に影響を与えることができる。通常の拡張的な財政政策の効果は、通貨価値の増大と純輸出の減少によって相殺される。固定相場制では、財政政策だけが所得に影響を与えることができる。通常の金融政策は、為替レートを公表水準に維持することにマネーサプライが用いられることによって有効性が失われる。
変動相場制:
金融政策を、雇用や物価の安定など、為替レートの維持以外の目標に対して自由に行使できる。
固定相場制:
為替レートを安定させることで、国際貿易の不確実性を軽減できる。また、一国の金融当局に自己規律を課し、マネーサプライの過度の増大を防ぐ一つの方法となる。
5)3目標同時達成の不可能性を説明しなさい。
一国が自由な資本移動、固定相場制、独立した金融政策のすべてを得ることはできない。この事実は「3目標同時達成の負可能性(impossible trinity)」あるいは「国際金融のトリレンマ」と呼ばれる。

各国は三角形の一辺を選択して、反対側の頂点を諦めなければならない。
応用問題
1)マンデル=フレミング・モデルを用いて、次のようなショックが生じたときに総所得、為替レート、貿易収支に何が生じるかを、変動相場制と固定相場制それぞれの場合で予測しなさい。解答には必ず適当な図表を付けなさい。
a 消費者の将来への不安が増して、消費が減少して貯蓄が増大する。
b ベンツが魅力的な車種を発表して、消費者が国産車よりも外国車を好むようになる。
c 現金自動預払機(ATM)が導入されて貨幣需要が減少する。
a

【変動相場制】
消費の減少は、IS*曲線を上方シフトさせる。

総所得
変わらない。
為替レート
e1からe2に上昇(減価)する。
貿易収支
消費の減少量と等量増大する。
【固定相場制】
消費の減少は、IS*曲線を上方シフトさせ、LM*曲線を為替レートを保持できるようシフトさせる。

総所得
Y1からY2に減る。
為替レート
変わらない。
貿易収支
変わらない。
b

【変動相場制】
外国の財・サービスの選好が高まると、IS*曲線を上方シフトさせる。

総所得
変わらない。
為替レート
e1からe2に上昇(減価)する。
貿易収支
変わらない。
【固定相場制】
外国の財・サービスの選好が高まると、IS*曲線を上方シフトさせ、LM*曲線を為替レートを保持できるようシフトさせる。

総所得
Y1からY2に減る。
為替レート
変わらない。
貿易収支
選好により輸入量が増え、減少する。
c

【変動相場制】
貨幣需要の減少はLM曲線を下方シフトさせるため、LM*曲線を右方シフトさせる。

総所得
Y1からY2に増える。
為替レート
e1からe2に上昇(減価)する。
貿易収支
NX(e)は、為替レートの上昇により増加する。
【固定相場制】
LM*曲線の変化は、為替レートが固定されているため打ち消される。

総所得
変わらない。
為替レート
変わらない。
貿易収支
変わらない。
2)小国開放経済が以下のような式で表現されている。
C = 50 + 0.75(Y - T)
I = 200 - 20r
NX = 200 - 50ε
$${\frac{M}{P} = Y - 40r}$$
G = 200
T = 200
M = 3000
P = 3
r* = 5
a IS*とLM*の曲線を導出して、図に描きなさい。
b 均衡の為替レート、所得水準、純輸出額を計算しなさい。
c 変動相場制を仮定する。もし政府が支出を50だけ増やすとすれば、為替レート、所得水準、純輸出、貨幣供給量に何が生じるかを計算しなさい。わかったことをグラフを使って説明しなさい。
d 次に、固定相場制を仮定する。もし政府が支出を50だけ増やすとすれば、為替レート、所得水準、純輸出、貨幣供給量に何が生じるかを計算しなさい。わかったことをグラフを使って説明しなさい。
a
IS*
Y = C(Y - T) + I(r*) + G + NX(ε)
= 50 + 0.75(Y - 200) + 200 - 20*5 + 200 + 200 - 50ε
Y = 1600 - 200ε
LM*
$${\frac{M}{P} = L(r*, Y)}$$
$${\frac{3000}{3} = Y - 40r = Y - 40*5}$$
Y = 1200

(=右上がりではない)のが若干気になる。
これは、問題が米ドルを想定しているためと思われる。
b
為替レート
Y = 1600 - 200εとY = 1200を解けば良いので、
ε = 2
所得水準
1200
純輸出額
NX = 200 - 50ε = 100
c

G = 250でIS*曲線を計算し直すと、
Y = 1800 - 200ε
為替レート
Y = 1800 - 200ε = 1200
ε = 3
所得水準
1200
純輸出
NX = 200 - 50ε = 50
貨幣供給量
3000のまま
d

為替レート
固定相場制なので2のまま。
所得水準
Y = 1800 - 200ε = 1400
純輸出
NX = 200 - 50ε = 100
貨幣供給量
$${\frac{M}{3} = Y - 40r = 1400 - 40*5 = 1200}$$
Mは増加して3600になる。
3)変動相場制下の小国開放経済が、貿易収支が均衡している下で、景気後退に陥っている。政策立案者が貿易収支の均衡を維持しながら完全雇用を達成したいとき、どのような金融政策と財政政策の組合せを選ぶべきか。それぞれの政策の効果を、必ずグラフで確認しなさい。
完全雇用を達成したい=生産量をショック前の値に戻したい、という問いとして理解する。このとき、変動相場制下で景気後退の影響を受けて減少している所得を増やすことができる施策は1つしかない(①)。すなわち、金融拡大政策である。
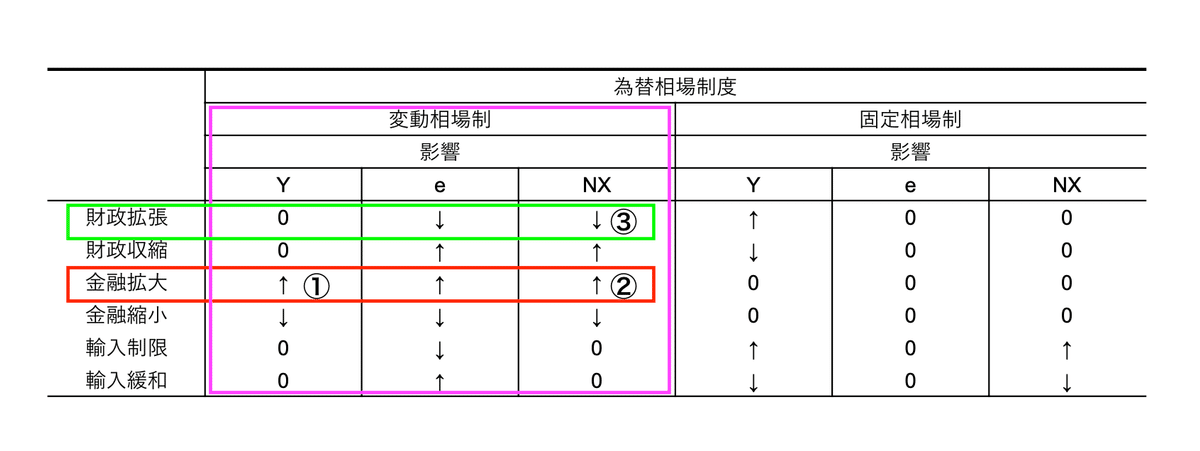
金融拡大政策を行うと、貿易収支は増加してしまう(②)。題意より、貿易収支の均衡を維持したいため、貿易収支の増加を打ち消すための施策を行う必要がある。これを満たすことができる施策も1つしかない(③)。すなわち、財政拡張政策である。
以上を総合し、
・マネーサプライの増大によりLM*曲線を右方シフトさせ(金融拡大)
・政府購入の増大や減税によりIS*曲線を下方シフトさせる(財政拡張)
政策を選択することとなる。

4)マンデル=フレミング・モデルでは世界利子率r*を外生的に決まる変数とみなす。この変数が変化するとき、何が生じるかを考えよう。
a 世界利子率の上昇をもたらすものは何か。(ヒント:世界は閉鎖経済である)
b 変動相場制の経済であれば、世界利子率が上昇すると、総所得、為替レート、貿易収支に何が生じるか。
c 固定相場制の経済であれば、世界利子率が上昇すると、総所得、為替レート、貿易収支に何が生じるか。
a
閉鎖経済において、利子率は貯蓄と投資関数の均衡によって定められた。
世界全体を閉鎖経済と捉えた場合、世界利子率は世界全体の貯蓄と世界全体の投資関数が均衡する値に収束する。
世界利子率の上昇は投資関数の上方シフトや貯蓄・投資の減少によってもたらされる。
b
IS*曲線について、
Y = C(Y - T) + I(r*) + G + NX(e)において、
r*が上昇するとIは減少し、Yは小さくなる。
したがって、IS*曲線は上方シフトする。
LM*曲線について、
r*が上昇するとLM曲線との交点が右方シフトするため、LM*曲線も右方シフトする。

総所得
Y1からY2に増える。
為替レート
e1からe2に上昇(減価)する。
貿易収支
NX(e)は、為替レートの上昇により増加する。
c
前問と同様、IS*曲線は上方シフトする。LM*曲線は、為替レートを一定に保てるよう左方シフトする。

総所得
Y1からY2に減る。
為替レート
変わらない。
貿易収支
NX(e)なので、変わらない。
5)アメリカの企業経営者や政策立案者は、アメリカ産業の「競争力」(自社や自国の製品を世界市場で有利に販売する力)に大きな関心を寄せている。
a 価格が固定されている短期には、名目為替レートの変化は競争力にどのように影響するか。
b アメリカ産業の競争力を強化したいが、総所得は変えたくないとしよう。マンデル=フレミング・モデルでは、アメリカの財政政策と金融政策をどのように組み合わせればよいか。それぞれの政策の効果を、必ずグラフで確認しなさい。
a
名目為替レートが上がる/下がる(減価/増価する)と、実質為替レートも上がる/下がる(減価/増価する)。
実質為替レートが減価すると競争力は上がり(外国財が相対的に高く、自国財が相対的に安くなり)、増価すると競争力は下がる(外国財が相対的に安く、自国財が相対的に高くなる)。
b
・競争力を強化=為替レートを上げる(減価させる)=変動相場制
・総所得に変化なし
・財政政策と金融政策の組み合わせ=輸入政策は考慮しない
の状況は、下図より
「財政収縮政策+金融政策を行わない」
の組み合わせとなる(生産を相殺するように2つの施策を組み合わせる組み合わせは存在しない)。

これをマンデル=フレミング・モデルに表すと以下のようになる。

なお、本問では議論しないが、
・固定相場制における為替レートのターゲット自体を減価させる
・輸入緩和政策単体での運用(財政政策・金融政策なし)
などの方法も考えられる。
6)所得が増加すると輸入が増加し、したがって純輸出が減少するとしよう。すなわち、純輸出関数は、
NX = NX(e, Y)
である。小国開放経済における拡張的な財政政策が所得と貿易収支に与える影響を次の為替相場制の下で検討しなさい。
a 変動相場制
b 固定相場制
その答えを表11-1の結果と比較しなさい。

a
拡張的な財政政策はIS*曲線を下方シフトさせる。

所得は変わらず、為替レートは下がり、純輸出は減る。これは、表11-1の結果と変わらない。
b
拡張的な財政政策はIS*曲線を下方シフトさせ、LM*曲線は為替レートの水準を維持するように右方シフトする。

所得は増大し、為替レートは変わらず、純輸出は所得の増大の影響により減少する。固定相場制においては、純輸出が所得の関数となることで表11-1とは異なる結果をもたらす。
7)貨幣需要が可処分所得に依存し、したがって貨幣市場を表す式が、
$${\frac{M}{P} = L(r, Y-T)}$$
であるとしよう。小国開放経済における減税が為替レートと所得に与える短期の影響を、変動相場制と固定相場制それぞれの場合について調べなさい。
【変動相場制】
減税はIS*曲線を下方シフトさせる。
減税によりTが小さくなるとY-Tは大きくなるため、LM曲線は下方シフトする。したがって、LM*曲線は右方シフトする。

為替レート
e1からe2に下降(増価)する。(LM*曲線のシフトが大きければ上昇(原価)することもある…?)
所得
Y1からY2に増える。
【固定相場制】
IS*曲線は下方シフトする。LM*曲線は、為替レートを固定させる方向にシフト(右方シフト)する

為替レート
変わらない。
所得
Y1からY2に増える。
8)貨幣需要に関わる価格には輸入財の価格が含まれており、輸入財の価格は為替レートに依存するとしよう。すなわち、貨幣市場は次式で示される。
$${\frac{M}{P} = L(r, Y)}$$
ただし、
$${P = λP_{d} + (1 - λ)eP_{f}}$$
ここで$${P_{d}}$$は外国通貨で測った国内財価格、$${P_{f}}$$は外国財価格、またeは為替レートである。したがって$${eP_{f}}$$は国内財価格で測った外国財価格である。パラメーターλは価格指数Pの国内財の割合である。国内財価格$${P_{d}}$$と外国通貨で測った外国財価格$${P_{f}}$$は短期では一定とする。
a 所与の$${P_{d}}$$と$${P_{f}}$$(通常のようにPではなく)に対してLM*曲線をグラフに描くとしよう。このLM*曲線はやはり垂直だろうか。理由も説明しなさい。
b このモデルで、変動相場制下の拡張的な財政政策の影響はどうなるか説明しなさい。標準的なマンデル=フレミング・モデルと比較しなさい。
c 政治的不安定性がその国のリスクプレミアムを上昇させ、利子率が上昇したとしよう。このモデルでは、為替レート、物価水準、総所得にはどのような影響があるか。標準的なマンデル=フレミング・モデルと比較しなさい。
a
eが上昇(減価)した場合、Pは大きく($${\frac{M}{P}}$$は小さく)なり、eが下降(増価)した場合、Pは小さく($${\frac{M}{P}}$$は大きく)なる。
したがって、LM*曲線は垂直ではなく右下がりになる。
b
IS*曲線は下方シフトする。

変動相場制下の拡張的な財政政策は為替レートをe1からe2に下降(増価)させ、所得をY1からY2に増やす。標準的なマンデル=フレミング・モデルとは、所得が変動する点で異なる。
c
リスクプレミアムの上昇により、IS*曲線もLM*曲線も上方シフトする。

為替レート
上昇(減価)する。
物価水準
為替レートが減価するため、上がる。
総所得
LM*曲線の傾きや利子率(リスクプレミアム)の変化の度合いによる。上がることもあれば、下がることもある。
標準的なマンデル=フレミング・モデルでは、LM*曲線が垂直であるため、リスクプレミアムの上昇は必ず所得の増加を意味する。本モデルでは、所得が増加するか否かは状況によって異なる。
9)マンデル=フレミング・モデルを用いて、カリフォルニア州(小国開放経済)についての次の問いに答えなさい。
a カリフォルニア州と主要な取引相手(アラバマ州、アラスカ州、アリゾナ州……)との間はどのような為替相場制度になっているか。
b カリフォルニア州が景気後退に陥ったとき、州政府は雇用を刺激するために金融政策や財政政策をとるべきだろうか。理由も説明しなさい(注:この問題では、州政府がドル紙幣を印刷できるものと仮定する)。
c カリフォルニア州がワシントン州からのワインの輸入を禁止すると、所得、為替レート、貿易収支に何が生じるか。短期と長期の両方の影響を考えなさい。
d マンデル=フレミング・モデルを、カナダではなくカリフォルニアに適用すると、そのモデルの有効性を弱める、カナダ経済とは異なるカリフォルニア経済の重要な特徴は何かを考えなさい。
a
互いにUSDを使っているため、為替相場は存在しない(物価水準の違いにより実質為替レートの違いは発生する可能性がある)。
b
政策効果を検討すると下図のようになる。

州政府は財政拡張政策のみ行うべきである。
c
貿易制限はIS*曲線を下方シフトさせる。短期ではLM*曲線は右方シフトするが、LM*曲線はやがて元の水準に戻る。

【短期】
所得
増える。
為替レート
変わらない。
貿易収支
増える。
【長期】
所得
変わらない。
為替レート
下降(増価)する(所得が元の水準に戻る過程で物価水準が上がり、実質為替レートは下降する)。
貿易収支
変わらない。
d
カリフォルニアと他州との関係は、本章のケース・スタディで示されたユーロ(共通通貨)を導入したヨーロッパ各国の関係によく似ている。
共通通貨の導入には、導入主体が独自の金融政策を実施できなくなってしまう(固定相場制になる)という欠点がある(本問では州政府は通貨発行権を有しているため全く同じ状況ではない)。
カナダは金融・財政政策の双方を自由に行使できるのに対し、カリフォルニアは財政政策しか行使できないという特徴が、マンデル=フレミング・モデルをカリフォルニア州に適用した際に有効性を弱めてしまう理由である。
別解として、章中に記載されているアメリカが大国である話(金融政策が世界利子率に影響を与えてしまうため、マンデル=フレミング・モデルはアメリカのような国を正確に表現できない)を援用するなどの方法も考えられる。ただし、これはマンデル=フレミング・モデル自体の限界であり、アメリカ以外の国を題材として本問を適用した場合は上記のような解答になるだろう。
応用問題(追加)
1)あなたは変動相場制下の大国開放経済の中央銀行の政策立案者だとしよう。あなたの目的は所得の安定であり、そのためにマネーサプライを調整する。この政策では、以下のショックのそれぞれに対して、マネーサプライ、利子率、為替レート、貿易収支に何が生じるか。
a 政府が財政赤字を減らすために増税する。
b 政府が外国車の輸入を制限する。
a
増税はIS曲線を下方シフトさせる。所得を安定させるためにLM曲線も下方シフトする必要がある。

マネーサプライ
所得を安定させるために増やす(増える)。
利子率
r1からr2に下がる。
為替レート
e1からe2に上がる(減価する)。
貿易収支
NX1からNX2に改善する。
b
保護貿易政策は純輸出需要を高め、純輸出関数を下方シフトさせるが、純輸出が変わらないため、他の市場には影響を与えない。

マネーサプライ
変わらない。
利子率
変わらない。
為替レート
e1からe2に下がる(増価する)
貿易収支
変わらない。
2)過去数十年間で世界経済はますます金融的に統合されてきた。すなわち、世界中の投資家は海外の金融的なチャンスをより積極的に活用するようになった。この展開が金融政策が経済に影響する力にどう作用するかを考えよう。
a 投資家が外国資産と国内資産を以前よりもより代替的と考えるようになると、CF関数の傾きはどうなるか。
b CF関数がこのように変化すると、IS曲線の傾きはどうなるか。
c IS曲線のこの変化は中央銀行が利子率をコントロールする力にどのような影響を与えるか。
d IS曲線のこの変化は中央銀行が国民所得をコントロールする力にどのような影響を与えるか。
a
より資本移動がスムーズな開放経済では、投資家が国内外で最も収益効率の高い資産を購入するようになるため、CF関数は水平方向に近づいていく(緩やかになる)。
b
緩やかになる。
c
IS曲線がより緩やかになると、一定量のマネーサプライの増減による金利のコントロール力はIS曲線がより急だった場合と比べて低くなる。
d
IS曲線がより緩やかになると、一定量のマネーサプライの増減による金利のコントロール力はIS曲線がより急だった場合と比べて高くなる。
3)大国開放経済の政策立案者が、総所得や為替レートを変化させずに、投資水準を引き上げたいと考えているとしよう。
a この目的を達成できるような自国の金融政策と財政政策の組合せは存在するか。
b この目的を達成できるような自国の金融政策、財政政策、貿易政策の組合せは存在するか。
c この目的を達成できるような自国および外国の金融政策と財政政策の組合せは存在するか。
a
所得が一定になるように金融政策と財政政策を組み合わせる場合、「収縮的な財政政策+拡張的な金融政策」or「拡張的な財政政策+収縮的な金融政策」の2通りであるが、いずれの場合も為替レートの変動は避けられない。したがって、金融政策と財政政策の組み合わせで総所得や為替レートを変化させずに投資水準を引き上げることはできない。
b
存在する。拡張的な金融政策と収縮的な財政政策の組み合わせにより、利子率を下げ、投資I(r)の水準を引き上げることができる。このことは、そのままの状態であれば為替レートの上昇(減価)を招くが、保護貿易政策を併用することで、為替レートも一定に保つことが可能となる。

c
存在する。自国は拡張的な金融政策と収縮的な財政政策の組み合わせにより、利子率を下げ、投資水準を引き上げる。このとき、外国が貯蓄を増大させるような財政政策をとると、外国の利子率は低下し、CF関数は下方シフトする。新たなCF関数と実質利子率との交点が、シフト前と同じ純輸出水準になれば、総所得も為替レートも変化させずに投資水準を引き上げられる。

4)この補論では変動相場制下の大国開放経済を考えた。次に、大国開放経済が固定相場制を採用していると仮定しよう。すなわち中央銀行はあらかじめ目標とする為替レートの水準を公表して、為替レートの均衡値が目標値に一致するように貨幣供給を調整することを約束するのである。
a 政府購入の増大のような財政拡張に対して、所得、利子率、貿易収支には何が生じるかを述べなさい。あなたの答えを固定相場制下の小国開放経済の場合と比較しなさい。
b 中央銀行が民間からの債券購入によって貨幣供給を拡大すると、所得、利子率、貿易収支には何が生じるかを述べなさい。あなたの答えを固定相場下の小国開放経済の場合と比較しなさい。
a
為替レートが固定されるためには、CF関数と実質利子率との交点が一定に保たれる必要がある(すなわち、国内利子率が一定)。
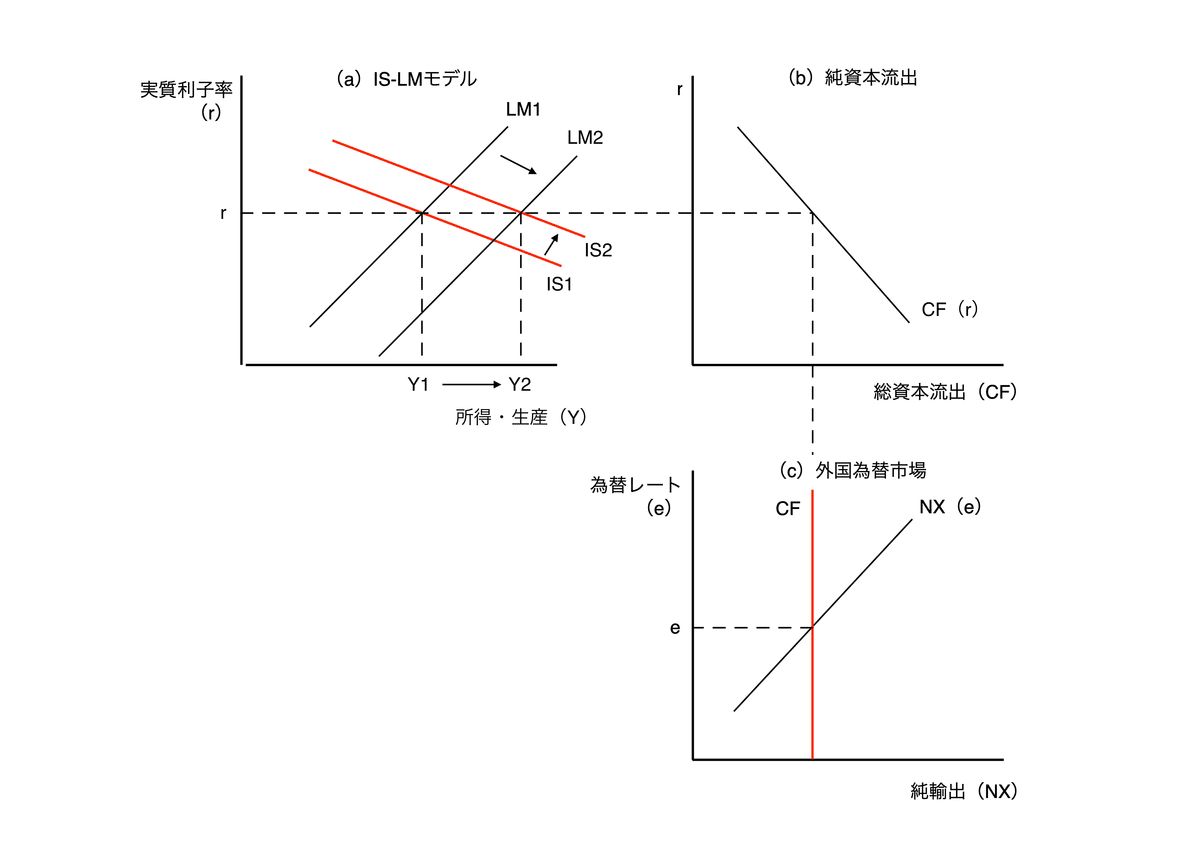
所得
Y1からY2に増える。
利子率
変わらない。
貿易収支
変わらない。
固定相場制下の小国開放経済の変化は以下のようになる(小国開放経済ではr = r*を仮定しているため利子率は変化しない)。

これは、大国開放経済の場合と同じである。
b
本問では中央銀行が政策主体であり、財政政策によって為替レートをコントロールすることはできない。拡張的な金融政策によってマネーサプライが増えると、為替レートを減価させてしまうため、中央銀行はその影響を打ち消すように自国通貨を買わなければならない。したがって、LM曲線の変化は巻き戻されることとなる。

所得
変わらない。
利子率
変わらない。
貿易収支
変わらない。
固定相場制下の小国開放経済の変化は以下のようになる。
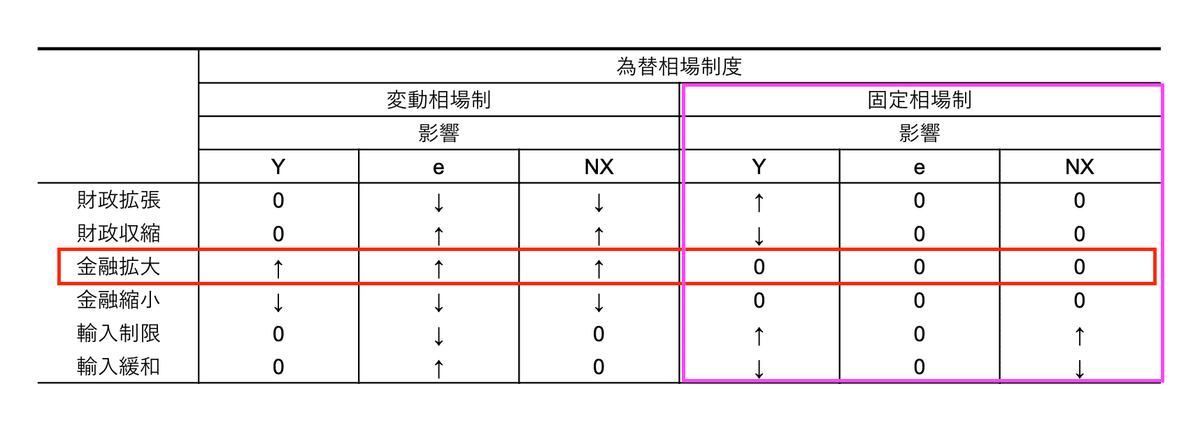
これは、大国開放経済の場合と同じである。
第十二章 総供給およびインフレーションと失業の短期的トレードオフ
復習問題
1)総供給の2つの理論を説明しなさい。それぞれの理論は市場のどのような不完全性に依存しているか。2つの理論の共通点は何か。
硬直価格モデル:
硬直価格モデルにおける市場の不完全性とは、財・サービス市場において企業が需要の変化に応じて価格をすぐには調整しない点である。
このモデルでは、企業が設定する諸価格に対してある程度の市場支配力を持っていることを仮定し、産出量の自然率からの乖離が物価水準の期待物価水準からの乖離と正の関係を持つことを示す。
不完全情報モデル:
不完全情報モデルにおける市場の不完全性とは、財・サービスの供給者が得られる情報が不完全であり(財の種類が多く、すべての価格を常に観察することができない)、情報の不完全性によって、彼らが一般的な物価水準の変化を相対価格の変化と混同してしまうことがある点である。
(情報の利用に限界があるのではなく、広範な情報を収集し処理する個々の能力に限界がある、とする研究もある)
このモデルでは、市場が清算的であることを前提とし、実際の物価が予想した物価を上回ると供給者が生産量を増やすことを示す。
これらのモデルはともに、市場の不完全性によって、経済の産出量が古典派の自然水準から乖離することを説明している。それぞれ別の理論的な根拠を持っているが、最後に帰着するのは、以下の短期総供給関数であるという点が共通している。
$${Y = \bar{Y} + α(P - EP) α > 0}$$
2)フィリップス曲線と総供給とはどのような関係にあるか。
フィリップス曲線と短期総供給曲線は、同一のマクロ経済の考えを表現しており、同じコインの裏表のような関係にある(短期総供給曲線への条件追加と式変形によってフィリップス曲線を導くことができる)。いずれも古典派の二分法(実質変数と名目変数の理論的な分離)をもたらす実質変数と名目変数の結びつきが、短期には崩壊することを示す。
短期総供給曲線は、産出量は物価水準の予期しない動きに関係することを表し、フィリップス曲線は、失業はインフレ率の予期しない動きに関係する(インフレと失業が負の関係にある)ことを表す。
3)なぜインフレは慣性を持つのか。
インフレが慣性を持つことは、適応的期待によって説明される。適応的期待とは、人々が最近に観察したインフレに基づいてインフレ期待を形成するという仮定である。過去のインフレ率は将来のインフレ期待に影響を与え、この期待が人々の設定する賃金や価格に影響する。インフレは、何かそれを止める力が作用しない限り動きを継続する。
4)ディマンドプル・インフレーションとコストプッシュ・インフレーションの違いを説明しなさい。
ディマンドプル・インフレーションは、高水準の総需要が循環的失業を自然失業率から乖離(低失業化)させることでインフレ率の上昇をもたらすことを指す。対して、コストプッシュ・インフレーションは、不利な供給ショックが生産コストを高め、インフレ率を上昇させることを指す。
5)どのような条件が満たされれば、景気後退を引き起こすことなく、インフレを抑制することが可能になるか。
景気後退を引き起こさないインフレ抑制を可能にするためには、合理的期待形成を仮定する必要がある。ここでは、人々が将来を予想するとき、政府の政策に関する情報を含むすべての利用可能な情報を最適に利用することを想定する。人々が合理的に期待を形成するならば、インフレーションは当初の印象ほど慣性的なものではなくなる。
政策立案者が信頼に足るインフレ抑制策を実施すれば、合理的な人々はこのコミットメントを理解し、期待インフレ率は速やかに低下する。その場合、インフレーションは失業の増大や産出量の減少を伴わずに(犠牲率の推計よりもはるかに少ないコストで)抑えることができる。
景気後退を引き起こさないディスインフレーションの条件は以下となる。
①インフレ抑制の計画が賃金や価格を決める労働者や企業が期待形成を行う前に発表されること。
②労働者や企業がこの発表を信頼すること。
双方の条件が満たされれば、この(インフレ抑制計画の)発表は即座にインフレーションと失業の短期のトレードオフを下方シフトさせ、失業率を上昇させることなくインフレ率を低下させると考えられる。
6)景気後退が自然失業率を引き上げる経路を2つ説明しなさい。
一部の経済学者は、景気後退が自然失業率を変化させることで、経済に恒久的な痕跡を残す多くのメカニズムを指摘した。履歴現象とは、自然率に長期的に持続する歴史的影響を与えることを指す言葉である。
経路1:景気後退が失業した人々を変化させる
労働者は失業すると優れた労働スキルを失い、景気後退が終わったときには求職能力が下がっているかもしれない。あるいは、長期にわたる失業は個人個人の仕事に対する意識を変えて、求職意欲を弱めるかもしれない。これらの変化は、求職過程に恒久的な阻害作用を及ぼし、摩擦的失業を増やす。
経路2:景気後退が賃金決定プロセスを変化させる
失業した人々は賃金決定プロセスにおける影響力を失う。たとえば失業によって労働組合の構成員としての地位を失う場合、賃金決定過程のインサイダーの一部がアウトサイダーになる。小さくなったインサイダーの集団が実質賃金の高さにより大きな関心を持ち、雇用にそれほど関心を払わなくなると、景気後退は実質賃金を均衡水準を超えて永続的に押し上げるようになり、構造的な失業者数を増やすことになる。
応用問題
1)硬直価格モデルを使って、次の特殊な場合の総供給曲線を描きなさい。これらのケースを、第八章で議論した短期の総供給曲線の場合と比較しなさい。
a すべての企業の価格が硬直的である(s = 1)。
b 望ましい価格が総産出量に依存しない(a = 0)。
硬直価格モデルについて、
$${P = EP + [\frac{(1-s)a}{s}](Y - \bar{Y})}$$(①)
であるから、
a
①にs = 1を代入すると、P = EP

これは第八章の場合と同じである。
b
①にa = 0を代入すると、P = EP
aと同じ結論となる。
2)次のようなフィリップス曲線の経済を想定しよう。
$${π = π_{-1} - 0.5(u - 5)}$$
a 自然失業率はいくらか。
b インフレと失業の関係を短期と長期について図示しなさい。
c インフレ率を4%引き下げるには、どれだけの循環的失業が必要になるか。オークンの法則を使って犠牲率を計算しなさい。
d 現在のインフレ率を6%としよう。中央銀行はそれを2%に引き下げたい。この目標を達成するシナリオを2つ書きなさい。
a
本問の想定は、フィリップス曲線$${π = Eπ - β(u - u^n) + v}$$から供給ショック(v)を除外したものである。したがって、$${Eπ = π_{-1}|β = 0.5|u^n = 5}$$となる(自然失業率は5%)。
b

c
$${π - π_{-1} = - 0.5(u - 5)}$$なので、インフレ率が4%下がるためには、8%の循環的失業が必要となる。
本書におけるオークンの法則では、失業率が1%上昇するごとに、実質GDPは平均して2%低下することが示された。
したがって、8%の循環的失業は実質GDPを16%引き下げる。
犠牲率とは、インフレ率を1%下げるのに実質GDPが年間何%失われなければならないかを示す数値である。
本問では、インフレ率4%を下げるために実質GDPが16%失われる必要があるため、犠牲率は、16 / 4 = 4%となる。
d
実質GDPが16%失われる期間についての設問である。
シナリオ1
単年度で16%の実質GDPが失われるケース(急激なディスインフレーション)
シナリオ2
4年間にわたり、4%ずつ実質GDPが失われるケース(穏やかなディスインフレーション)
3)次のようなフィリップス曲線の経済を考えよう。
$${π = Eπ - 0.5(u - 6)}$$(①)
人々は次式のように過去2年間のインフレ率の加重平均を取ってインフレ期待を形成する。
$${Eπ = 0.7_{π - 1} + 0.3_{π - 2}}$$(②)
この経済のオークンの法則は、
$${(Y - Y_{-1}) / Y_{-1} = 3.0 - 2.0(u - u_{-1})}$$(③)
経済は5%の安定したインフレ率の下で、自然失業率の状態にあるとする。
a この経済の自然失業率はいくらか。
b この経済が直面するインフレーションと失業の短期のトレードオフを図示しなさい。経済が始まる場所を点Aとして表示しなさい(点Aの数値の記入を忘れないように)。
c 総需要の減少によって景気後退が生じて、失業率が自然率を4%上回る点まで増大した。その年に経済が経験した動きを点Bとして問bの図の中に表示しなさい(再び、数値の記入を忘れないように)。
d 失業はこの高い水準に2年間(最初の年は問cに書いた通りで、さらにもう1年)とどまって、その後に自然率に戻るとしよう。景気後退の2年前から10年間について、失業、インフレーション、期待インフレ、産出成長率を示す表を作成しなさい(この計算にはコンピューターのスプレッドシートを使うのが最善)。
e 上の問bで使った同じ図に、この10年間の終了時点に経済が直面する短期のトレードオフを点Cとして図示しなさい(再び、数値を記入するように)。
f 景気後退の前の均衡を新しい(第10期目の)長期均衡と比較しなさい。インフレーションはどれほど変化したか。この移行期に何パーセント分の産出が失われたか。この経済の犠牲率はいくらか。
a
6%
b
問題文より、自然失業率下のインフレ率は5%
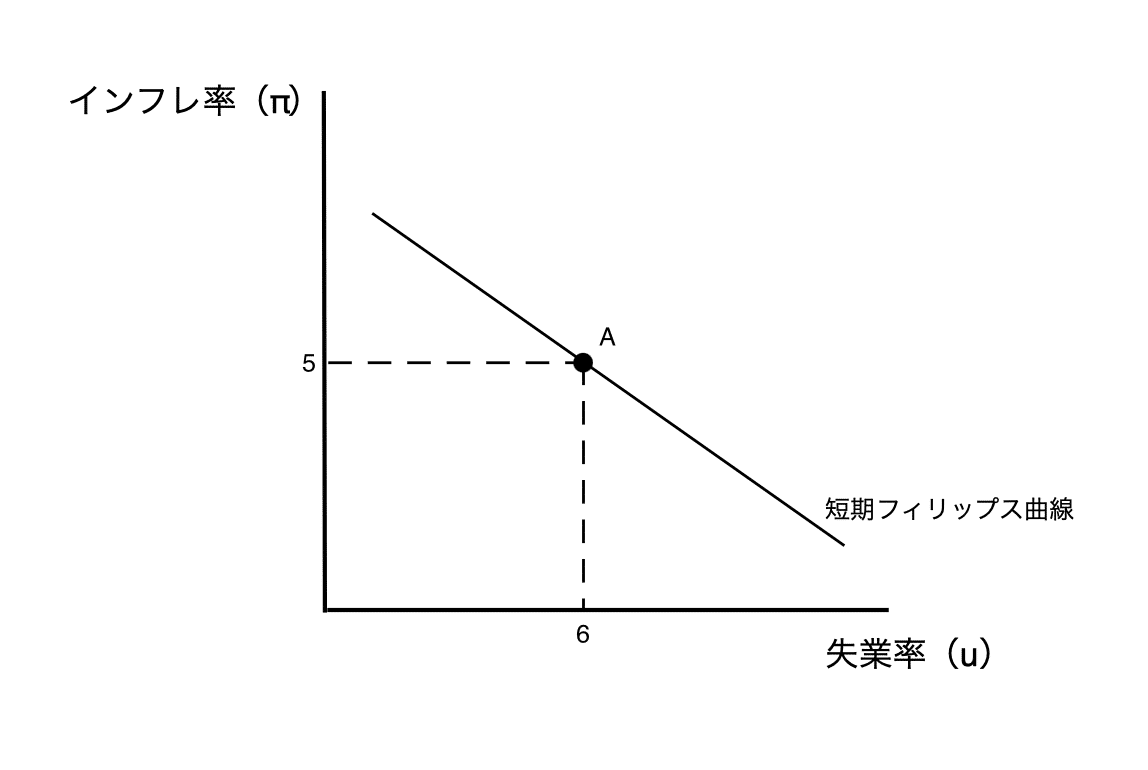
c
安定している前提から、1年前・2年前のπはともに5%とする。
②より、Eπは5%、①より、π = 5 - 0.5(10 - 6) = 3%とわかる。

d

実際にはこうはならなさそう。。
e

f
インフレーション
3.08%低下した。
GDP
8%失われた。
犠牲率
8 / 3.08 ≒ 2.6%
4)合理的期待アプローチによれば、政策立案者のインフレ抑制の約束を皆が信じる場合、インフレ抑制のコスト(犠牲率)は国民が政策立案者の意図に疑問を持っている場合よりも低い。なぜそういえるのか。どのようにすれば政策の信頼性を高められるのだろうか。
フィリップス曲線において、インフレ期待はインフレ率の変数であった($${π = Eπ - β(u - u^n) + v}$$)。合理的期待アプローチでは、人々がインフレ期待を形成する際に、金融・財政政策の情報も最適に利用される。
人々が政策立案者のインフレ抑制の約束を信じる場合、この約束はインフレ期待に低コストで織り込まれ、実際のインフレ率もそれに追随するが、人々が政策立案者の意図に疑問を持っている場合、インフレ期待は前者ほど変化しない(したがって、インフレ率も前者ほど変化しない)。フィリップス曲線の右辺が同程度小さくなるためには、循環的失業が増える(犠牲率が前者に比べて上がる)必要がある。
政策の信頼性を高めるのは難しい議論である。本書では、ポール・ボルカー連邦準備議長の「断固とした姿勢が十分に信頼できるものであったため、インフレ期待に直接影響を与えた」という例が示された。
現代ではフォワードガイダンスのようなアプローチが取られるなど(アメリカでは途中で撤廃されてしまったが…)、様々な方策が試されている。
5)経済が当初、長期均衡の位置にあるとしよう。ここで、中央銀行がマネーサプライを増大したとする。
a その結果生じたインフレが予想外のものであったと仮定して、拡張的な金融政策によって引き起こされるGDP、失業、インフレの変化を記述しなさい。あなたの結論を3つの図(IS-LMモデル、AD-ASモデル、フィリップス曲線)を用いて説明しなさい。
b 上とは逆に、インフレが予想されるものだった場合、拡張的な金融政策によって引き起こされるGDP、失業、インフレの変化を記述しなさい。上と同様に、あなたの結論を3つの図(IS-LMモデル、AD-ASモデル、フィリップス曲線)を用いて説明しなさい。
a

GDP
マネーサプライの増大は、短期ではLM曲線を下方シフトさせるが、長期ではLM曲線は元の水準に戻る。また、短期ではAD曲線の上方シフトにより増大するが、長期では総供給は自然率水準に戻る。
IS-LMモデルでも、AD-ASモデルでも、マネーサプライの増大はGDPを短期では増大させるが、長期では元の水準に戻る(IS-LMモデルから、金利が一時的に低下し、元の水準に戻ることが、AD-ASモデルから、価格は元の水準には戻らず上昇することがわかる)。
失業
短期ではGDPの増大により、失業も短期では自然率水準を下回るが、長期では期待インフレ率の上昇とともに短期フィリップス曲線が上方シフトし、自然率水準に戻る。
インフレ(参考)
短期では期待インフレが織り込まれる前の短期フィリップス曲線上の失業率に沿った水準に移動し(π2)、長期ではシフト後の短期フィリップス曲線と長期フィリップス曲線との交点に収束する(π3)。
b

GDP
(自信ないです。正確にはこういう現象が起きるのではないかという気はしますが私の理解力を超えていました)
IS-LMモデルについて、IS曲線は期待インフレを織り込む形で上方シフトする(Y = C(Y - T) + I(i - Eπ) + G)。
期待インフレは価格に織り込まれるため実質貨幣残高は変化せず(MもPも増大し$${\frac{M}{P}}$$が一定のまま)、LM曲線は、短期的な下方シフトを起こすことなく長期均衡水準に向かう。この変化は瞬時に起こると思われる(GDPに影響を与えない)。
AD-ASモデルについて、SRASは期待インフレを織り込む形で上昇し、AD曲線はマネーサプライの増大により上方シフトするため、短期的なGDPのシフトを起こすことなく物価水準のみが上がる。(GDPは自然率水準のまま)
失業
期待インフレ率が瞬時に上昇すると、短期フィリップス曲線はすぐに上方シフトし、失業率に変化を与えない。
インフレ
短期フィリップス曲線の上方シフトは、インフレ率を上昇させる。
6)人々が合理的な期待を形成して、経済は硬直価格モデルで記述されるとしよう。以下の主張のそれぞれが正しいかどうか説明しなさい。
a 貨幣供給の予期しない変化だけが実質GDPに影響する。価格が設定されるときに予期されていた貨幣供給の変化はいかなる実質効果も持たない。
b 中央銀行の貨幣供給の決定と人々の価格設定が同時で、その結果、誰もが経済状態について同じ情報を保有するなら、産出を安定させるために金融政策を体系的に用いることはできない。したがって、貨幣供給を一定に維持する政策と貨幣供給を経済状態に合わせて調整する政策は、実質的に同じ効果を持つ。(これは政策無効命題と呼ばれる)
c もし中央銀行が、人々の価格決定から十分時間をとって、貨幣供給を設定すれば、中央銀行は経済状態についてもっと多くの情報を収集できる。その場合、産出を安定させるために金融政策を体系的に用いることができる。
a
「$${Y = \bar{Y} + α(P - EP) α > 0}$$」において、P = EPの場合(予期された貨幣供給の変化 = 予期された価格の変化 = 設定価格)、$${Y = \bar{Y}}$$となる。したがって、命題は正しい。
b
前問(応用問題5のb)のように、価格への反映が即時であれば産出は自然率に固定されるため、金融政策は産出に対して影響を与えることはできず、貨幣供給を一定に維持する政策(=LM曲線をシフトさせない政策)と(産出に対する影響という点で)実質的に同じであると言える。したがって、命題は正しい。
余談ながら、これをルーカスモデルというらしい。(最近は政策無効命題は否定されていたりする)。
c
十分な時間を空けることで、人々の合理的期待の経済に対する織り込みが完了し、その状況を観測した上で政策を打つことができるという解釈をするのであれば、この命題は正しいように思える(人々の期待の織り込みが終わっていない段階で政策を打ち続ける状態と比較すれば体系的になるだろうと思われる)。ただし、時間を空けることで経済状況が悪化する(方向に人々の期待が傾く)可能性もあり、なんともいえない設題である。
7)次のようなフィリップス曲線
$${π = π_{-1} - 0.5(u - u^n)}$$
の経済を考えよう。自然失業率は過去2年間の失業率の平均
$${u^n = 0.5(u_{-1} + u_{-2})}$$
で与えられるとする。
a 自然失業率はなぜ(上式で仮定されているように)最近の失業率に依存するのか。
b 中央銀行がインフレ率を恒久的に1%引き下げる政策を実施するとしよう。この政策は、時間とともに失業率にどう影響するか。
c この経済の犠牲率はいくらになるか。理由も説明しなさい。
d これらの式はインフレと失業の短期および長期のトレードオフについて何を意味するか。
a
上式では履歴現象をモデルに組み込もうとしていると思われる。履歴現象を考慮すると、失業率の自然率水準は、直近の失業率の影響を受け変動する。
(適応的期待に基づいて企業が採用活動を行うため、のような説明も可能と思われる)
b
インフレが1%下がることが恒久的に続くため、$${π = π_{-1} - 0.5(u - u^n)}$$における$${u - u^n}$$の部分が2になればいいことがわかる。この関係は、たとえば$${u - u^n = u_{1} - u_{1}^n = u_{2} - u_{2}^n = ……. = 2}$$のように、恒久的に維持されることがわかる。
ここで、任意の値を入れて推移を観察してみる。

インフレが恒久的に1%下がる環境では、失業率と自然失業率は常に増加し続け、その増加幅はある値(1.3333….)に漸近することがわかる(ただし、失業率が100%を超えるのは原理的に不可能なので、モデルに組み込まれていない変数など諸々の限界はありそうに思われる)。
c
オークンの法則(本書ver.)では、失業率が1%上昇するごとに、実質GDPは平均して2%低下する。
2%の循環的失業は実質GDPを4%引き下げる。
インフレ率1%を下げるために実質GDPが4%失われる必要があるため、犠牲率は4%となる。
d
履歴現象を考慮しないモデルにおいては、インフレと失業の間には短期のトレードオフが存在するが、長期でのトレードオフは存在しなかった(長期においては、経済は古典派モデルで記述される自然率水準に回帰する)。
しかし、履歴現象を考慮するモデルにおいては、インフレと失業の間には、短期だけでなく、長期のトレードオフが存在する(景気後退は自然失業率を変化させるため、経済に恒久的な痕跡を残す=インフレを継続的に下げるためには失業率が上がり続ける必要がある)。
8)一部の経済学者は租税が労働供給に重要な影響を及ぼすと考えている。彼らによると、増税は人々により少なくしか働きたくない気を起こさせ、減税はより多く働きたい気持ちを引き起こす。この効果が租税変更のマクロ経済分析にどのように影響するかを考えよう。
a もしこの考え方が正しければ、減税は産出の自然率にどのように影響するか。
b 減税は総需要曲線にどのように影響するか。長期の総供給曲線、短期の総供給曲線にどのように影響するか。
c 減税は短期の産出と物価水準にどう影響するか。あなたの答えは労働供給への効果がない場合と較べて、どう異なるか。
d 減税は長期の産出と物価水準にどう影響するか。あなたの答えは労働供給への効果がない場合と較べて、どう異なるか。
a
労働の総量が増えるため(Y = F(K, L))、産出の自然率は増加する。
b
総需要曲線
労働供給を考える前提での減税は対家計である。家計では減税により可処分所得が増えるため、家計の消費は増加する(C = C(Y - T))。消費が増加するため、減税はAD曲線を上方シフトさせる。
長期の総供給曲線
問aより、$${\bar{Y}}$$が増加するため、右方シフトする。
短期の総供給曲線
本章では硬直価格モデルと不完全情報モデルの2つを議論した。硬直価格モデルにおいては価格は硬直的であるため、短期総供給曲線はシフトしない。不完全情報モデル(市場が清算的であることを仮定するモデル)では、有利な供給ショックが発生したと捉えられるため下方シフトする。

c

硬直価格モデル
短期の産出は増える。物価水準は変わらない。労働供給への効果がない場合と同じである。
不完全情報モデル
短期の産出は増える。物価水準は短期総供給曲線への労働供給への影響次第であるが、価格が伸縮的で労働供給への効果がない場合と比較すると、産出の増加量は高く、価格上昇量は低くなる。
d

硬直価格モデルも不完全情報モデルも長期では同様の影響となる。
長期の産出は長期供給曲線の水準に収束する。物価水準は、長期供給曲線と総需要曲線との交点に収束する。労働供給への効果がない場合は長期供給曲線がシフトしない(生産の自然率水準が変化しない)ため、生産は元の水準に回帰し、物価水準は必ず上がるが、本モデルでは長期供給曲線が右方シフトするため、元の水準よりも生産が増加し、物価水準については長期供給曲線のシフト次第で収束する位置が変わるという点が異なる。
9)労働統計局のWebサイト( https://www.bls.gov )をみなさい。過去5年について、各年の全品目の消費者物価指数で測ったインフレ率(headline inflation と呼ばれているもの)と、食料品とエネルギーを除くCPIで測ったインフレ率(core inflation と呼ばれているもの)を探し、この2つのインフレ率を比較しなさい。それらはなぜ異なっているのか。この違いは総供給曲線のシフトと短期のフィリップス曲線のシフトについて何を示しているのか。

落差が激しい方がAll Items、比較的なだらかな方がAll Items less food and energy。
食料品とエネルギーは、CPI全体と比べて供給制約の関係などの影響で変動を受けやすいものと思われる。これらの品目は、総供給曲線に対しては供給ショックとして働きやすく、品目全体よりも、より供給曲線を上下させる原因となりやすい。また、期待インフレ率への影響という点で、よりフィリップス曲線を上下させる原因となりやすい。

https://www.oanda.jp/lab-education/dictionary/cpi/
応用問題(追加)
1)このすべてのモデルの親モデルの特殊ケースをもう少し考えよう。以下のような特定のモデルを得るには、この包括的モデルから出発して、どのような追加の仮定が必要だろうか。
a 第六章補論の古典派の大国開放経済モデル
b 第九章前半のケインジアンの交差図
c 第十一章補論の大国開放経済のIS-LMモデル
a
EP = P, L(i, Y) = (1/V)Y, CF(r - r*) = CF(r)
b
αが無限大, CF(r - r*) = 0, $${I(r) = \bar{I}}$$
c
αが無限大, CF(r - r*) = CF(r)
