基本情報技術者試験 の独習
ひばりが丘PARCOの本屋で『基本情報技術者パーフェクトラーニング過去問題集(山本三雄・著)』を買ってきたら 雑談なしのリファレンスになっていて つらいので、雑談形式で だらだらと書いてみる
本屋の棚には 計算の練習の本ばっかりあって、読み物の本がないのはどうしたものか
進数の変換
世界4大文明の4つの国がどこかご存じだろうか?
細かくぶれることがあるが大筋で メソポタミア、エジプト、インダス、黄河 の4つだろう。
なお この4つの文明はもう滅びている。
世界4大文明とは、歴史に書かれる文明のうち最初に別々の起源をもって発生した4つの文明ぐらいの意味だ
この中のメソポタミアでは 借金をつけた帳簿の記録とか、なんかよくわからん記録は、粘土板(ねんどばん)に書かれていたようだ。
粘土をご存じだろうか? 平成初期の日本の小学校で捏ねた粘土とは違うようだが、文字を書き直そうと思えば、表面を削り取って さらに掘ればいいらしい
https://www.eurasia.city.yokohama.jp/cuneiform/about.html
なんで紙と墨ではなく、粘土と葦(で作ったペン)を使ったかだが、歴史の人がよく言うんだが、住んでるとこでよく取れる素材を使ってるだけと考えるのが ふつうらしい
粘土板に書かれる文字の話。粘土板の上を葦で掘って字を書くとき、曲線は掘りにくいので自然と直線的に掘ることになるが、そのとき空いた穴の形を後世の人が見たとき楔形(くさびがた)に似ていたので、楔形文字と呼ばれる。だからメソポタミア文明と楔は関係ない
もちろん、数字も楔形で書かれる。
このとき使われる数字は、メソポタミア文明のバビロニア地方の名前を持った バビロニア数字 の記録が残っていて、現代人が見ると、小数点(※)がなく、
そして 現代でも時計の秒針に残っている60進法を使っている
※小数点 … のちにジョン・ネイピアさんが創る
もっというと メソポタミアの数字は60進数ではあるが、
細かくみると 10進数×6進数 みたいな形をしている
「なんだ バビロニア数字 こんな不便そうなの使ってんのか」と試しにバビロニア数字を使ってみたことがあるが
「思わぬ数が綺麗に割り切れてめっちゃ便利!なんで現代人は60進数を使っていないのだろう」
と思った。
10進数の10は6で割り切れないが、
60進数の 𒐕〃(60 ※注)は 𒐋(6)で割り切れて 𒌋(10)になる
※注 … ゼロがないので仕方なくわたしが 〃 の字を置いただけ。不便だなあ
やってみれば分かるが 𒐕(1)が 𒐗(3)で割り切れるのとかビックリする ヤバい。
また、200秒は 𒐕𒐕𒐕 𒌋𒌋 みたいな感じで書く。60が3個と10が2個。
この数を表記した時点で200秒は3分と20秒とすぐ分かる
バビロニア数字には ゼロ(※)が無いのも面白い
※ゼロ … のちにインド人が創る
このようにメソポタミア文明のバビロニア数字は60進法を使っているし、
現代のアラビア数字は10進法を使っている。
また現代で使われているパソコンは 2進法、8進法、16進法をよく使う
👆 パソコンで2進法、8進法や16進法がよく使われる経緯
こうなってくると 2進法、8進法、10進法、16進法、60進法を それぞれ変換したくなってくる。
人類は 進法を1つに統合するのではなく、変換するということを選んだ
2進法 というのは 0、1 という数字だけがあり、
1 から もう1つ増えたら 10 と表記する、というものだ
8進法 というのは 0、1、2、3、4、5、6、7 という数字だけがあり、
7 から もう1つ増えたら 10 と表記する、というものだ
10進法 というのは 0、1、2、3、4、5、6、7、8、9 という数字だけがあり、
9 から もう1つ増えたら 10 と表記する、というものだ
16進法 というのは 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F という数字だけがあり、
F から もう1つ増えたら 10 と表記する、というものだ
60進法 というのは
𒐕、𒐖、𒐗、𒐘、𒐙、𒐚、𒐛、𒐜、𒐝、
𒌋、𒌋𒐕、𒌋𒐖、𒌋𒐗、𒌋𒐘、𒌋𒐙、𒌋𒐚、𒌋𒐛、𒌋𒐜、𒌋𒐝、
𒎙、𒎙𒐕、𒎙𒐖、𒎙𒐗、𒎙𒐘、𒎙𒐙、𒎙𒐚、𒎙𒐛、𒎙𒐜、𒎙𒐝、
𒌍、𒌍𒐕、𒌍𒐖、𒌍𒐗、𒌍𒐘、𒌍𒐙、𒌍𒐚、𒌍𒐛、𒌍𒐜、𒌍𒐝、
𒐏、𒐏𒐕、𒐏𒐖、𒐏𒐗、𒐏𒐘、𒐏𒐙、𒐏𒐚、𒐏𒐛、𒐏𒐜、𒐏𒐝、
𒐐、𒐐𒐕、𒐐𒐖、𒐐𒐗、𒐐𒐘、𒐐𒐙、𒐐𒐚、𒐐𒐛、𒐐𒐜、𒐐𒐝 という数字だけがあり、
𒐐𒐝 から もう1つ増えたら 𒐕〃 と表記する、というものだ
この法則を見ると、(アラビア数字だけ見れば)すべての進法は10進数に見える。
この真実に気づいた人は
「10進法のことは A進法 と呼ぶべきだ!」
と強く主張するが だいたい こういう人は主流にはならない
ここまで来ると気づいた人がいるかもしれない。
結局 進数の変換 とは 位取りの方法の違い でしかない。
詳しく見ていこう
👇 以下、初見では難しいと思うので、10進法の説明まで読み流してほしい
2進法で 10.1 という数字があったとしよう。
これは
10.1 = 1 × 10 +
0 × 1 +
1 × 0.1
ということだ
8進法で 12.3 という数字があったとしよう。
これは
12.3 = 1 × 10 +
2 × 1 +
3 × 0.1
ということだ
10進法で 12.3 という数字があったとしよう。
これは
12.3 = 1 × 10 +
2 × 1 +
3 × 0.1
ということだ
16進法で 12.3 という数字があったとしよう。
これは
12.3 = 1 × 10 +
2 × 1
3 × 0.1
ということだ
60進法で 𒐕 𒐖 𒐗 という数字があったとしよう。
これは
𒐕 𒐖 𒐗 = 𒐕 × 𒐕〃 +
𒐖 × 𒐕 +
𒐗 × 〃𒐕
ということだ
👆 現代人のわたしたちには10進法以外は 見づらいかもしれないが、
やってることは全部同じで、ここで紹介したのは 位取り だ。
なんで見づらいかというと、
10、 1、 0.1 といった数字が見づらいだけ でしかない
この視覚の問題を解決すると 進法の変換 は何も考えなくても 見えれば、あとは計算しか残らない
2進法 10進法
1000 2×2×2
100 2×2
10 2
1 1
0.1 1/2
0.01 1/2/2
8進法 10進法
1000 8×8×8
100 8×8
10 8
1 1
0.1 1/8
0.01 1/8/8
10進法 10進法
1000 10×10×10
100 10×10
10 10
1 1
0.1 1/10
0.01 1/10/10
16進法 10進法
1000 16×16×16
100 16×16
10 16
1 1
0.1 1/16
0.01 1/16/16
60進法 10進法
𒐕〃〃〃 60×60×60
𒐕〃〃 60×60
𒐕〃 60
𒐕 1
〃𒐕 1/60
〃〃𒐕 1/60/60
👆 こうしてみると 「10」の位に置いた数字のことを 「何」進法と呼んでいるだけだと分かる
このときの、十の位にある数字の 1 と、一の位にあるインド人が創った 0 という2つの数字は、
数字というシステムを成り立たせる上で まず重要だな、と分かる。
2とか3とか、AとかBより、まずは 1と0 が大事
この数字の 1と0 の機構にハマった人に ゴットフリート・ライプニッツ という数学者がいる。
この人も後世になって実は計算機の発展にとって重要な人だったのではないかと再評価されたような人で、たぶん300年間ぐらい、一部の人に一目置かれていただけで多くの当時の人からは、この人は何をやってたんだろうワケワカラン、とか思われていたのだろうと思う。
情報処理をやってると、いろんなとこでたびたび名前が出てくる
じゃあ16進数の 0.C を10進数に変換してみろよ、とか問題が出てきたら、16進数の C は10進数で12なのと、
16進数の0.1は10進数では1/16だから、
その12倍だけ見て 10進数では12/16だと分かるので
約分して3/4、これって0.75だと分かる
進法の変換の説明おわり
論理式
括弧(かっこ)というと
( ) [ ] { }👆 こういうやつだ。括(くく)る弧という なるほど納得な名前をしている
しかし 括る記号は いつの頃なのか昔のヨーロッパでは 線 だったこともあるようで …
👆 活線(かっせん) という言葉もある。活線というのは …
----- -----
2 + 3 × 5 + 7👆 線を引くことで、括弧と同様の働きをするもののようだ
現代では 分数の分母や、ルート などで 横線を引っ張ることがあり、
括線の気分を味わえる
また、それ以外でも 括線の気分を味わえるものとして、論理式の否定記号 がある。NOT (ノット)だ
-------------
True Or False👆 上図では なんや上に線が引っ張ってある、これが否定記号で、
この式全体の読み方は 日本語で言うと、「『真だ、または偽だ』ではない」とでも読める
しかし、論理式には 論理学でいうところの読み方 とでもいうようなものがある。ルールを教えてもらって練習しておかないと、読めないと思う
また、論理学では、意味が似ていて、何が違うのか?というような記号がいっぱい出てくる
形式論理学 電子工学 日本語 英語
⊤ 1 真 TRUE
⊥ 0 偽 FALSE
∧ ・ 論理積 AND
∨ + 論理和 OR
¬ ※括線 否定 NOT
⊻ ※〇の中に+ 排他的論理和 XOR, Exclusive Or
∣ ※注1 否定論理積 NAND
※無い? ※注2 否定論理和 NOR
※注1 ------
A ・ B
※注2 ------
A + B👆 わたしたちが やっている情報処理(Information Processing)は 電子工学(Electronics) で使うんで、電子工学の 論理記号を使う
形式論理学(Formal Logic)って何なのか? とか、
形式論理学と 電子工学で 何で似たようなことやってて 記号がバラバラなのかとか、
これも 起源が異なって 別のところで始まったから、ぐらいでしかない
もっというと 論理回路(Logic Gate)とか C言語の論理演算子とか
似たようなのがある
とりあえず、 TRUE や FALSE といった項(こう;Operand)と、
AND, OR, NOT, XOR, NAND, NOR といった演算子(えんざんし;Operator)の合計8個が 何なのかを覚えてしまえば 論理式 を利用し、自分のものとすることができる
演算子は ENOR とか他にもあるが、ここでは省略する
1
0👆 項 というのは基本的に TRUE か FALSE しかない。
TRUE を 1、 FALSE を 0 と書くことはよくある
NOT ★👆 NOT 演算子は、1つの項だけに効くので、単項演算子と呼ぶ
◆ AND ★
◆ OR ★
◆ XOR ★
◆ NAND ★
◆ NOR ★👆 それ以外の演算子は 2つの項に効くので、2項演算子と呼ぶ
単項演算子にしろ、2項演算子にしろ、その式を評価(※計算すること)した結果は また 項 になる
NOT 1 👉 0
NOT 0 👉 1👆 NOT 1 を評価したら 0 になるし、
NOT 0 を評価したら 1 になる
この書き方では めんどくさいので 表の書き方を決めておく。
以下の表は、最終的には覚えておく必要はあるが、今は意味が分からないだろうから読み流してほしい
____
P P
---- -----
0 1
1 0
👆 NOT は、 0 と 1 を ひっくり返す だけ
P Q P ・ Q
---- ---- --------
0 0 0
0 1 0
1 0 0
1 1 1
👆 AND は、 P と Q の両方が 1 のときだけ 1。それ以外は 0
P Q P + Q
---- ---- --------
0 0 0
0 1 1
1 0 1
1 1 1
👆 OR は、 P と Q のどちらかが 1 だったら 1、そうでなかったら 0
P Q P XOR Q
---- ---- --------
0 0 0
0 1 1
1 0 1
1 1 0
👆 XOR は、 P と Q の片方だけが 1 だったら 1、そうでなかったら 0
_______
P Q P ・ Q
---- ---- --------
0 0 1
0 1 1
1 0 1
1 1 0
👆 NAND は、 AND の 0、1 をひっくり返した だけ
_______
P Q P + Q
---- ---- --------
0 0 1
0 1 0
1 0 0
1 1 0
👆 NOR は、 OR の 0、1 をひっくり返した だけ
なお、PとQは交換可能だ。
つまり、P+Q を Q+P に順番を入れ替えても評価した結果は同じになる。これは、小学校で習う+(足し算記号)、×(掛け算記号)でも同じだ。確認してほしい
この表を覚えることができれば、あとは計算するだけで 論理式 は利用できる
例えば、赤い鳥、緑色の鳥、青い鳥 の3匹だけが存在する世界だとして、
赤い鳥と 緑色の鳥を見た時だけ吠えろ、と指示したいときは、
赤い鳥 + 緑色の鳥 を見たら吠えろ______
青い鳥 を見たら吠えろ👆 上記のような感じで指示を出したらいい。書き方は何通りかあると思うが、どういう書き方が1番いいかは そのときのいろんな場合によるんで、がんばってほしい
なんにしろ、 True だとか 1 というのは、スイッチオン みたいな感じだ
しかし、同じことを いろんな書き方ができるんだったら、
プログラムのチェックが めっちゃ難しくない?
と思われると思うんだが、実際難しく、
短く書いたら読みずらいし、長く書いたら読みたくないとか、
簡単な方法は記憶力を酷使するとか、悩みにキリがなく、
まあ がんばれ という言葉で丸投げしておこう
ド・モルガンの法則
あまりに がんばりが要求される論理式だが、少し助けてくれる法則を発見した人がいて、その法則を ド・モルガンの法則 と呼ばれるものがある
数学の著名人としては ド・モルガン という名前の人は2人いる とかいう話しもあるが、そのもう1人の方は わたしは知らない
👇 この ド・モルガンの法則 というものは、2通りのことを言っている
「P でも、Q でも、どちらでもない」ということは、
「P ではなく、かつ、Q ではない」と言ってるのと同じだ
「Pでもあり Qでもあるようなものはない」ということは、
「Pではないか、Qではないか、またはその両方だ」と言ってるのと同じだ
👆 なんにしろ 難しい。 Pに阪神ファン、Qに巨人ファンを入れれば
少しイメージしやすくなるか?
_____ ___ ___
P + Q ということは、 P ・ Q と言ってるのと同じだ
______ ___ ___
P ・ Q ということは、 P + Q と言ってるのと同じだ👆 論理式にすると上記の通り
このブログ(Note)では書きづらいが、ド・モルガンの法則を2回しろ、とかいうような意地悪問題が出てくることがあるが、確かに世の中は制限なく意地悪問題とか出てくるので つらいががんばれ と言うしかない
ニュートン法
わたしたちが小学校や中学校の黒板で数学を説明されるとき見ているようなグラフは 紀元前3世紀のギリシャ人も見ていたようなグラフで、人類は2300年近く 同じ図形の問題を考えているんだが、それを ユークリッド空間 とか呼ぶ。ユークリッド空間って何? と思えば、いつものやつ、ぐらいに思っておけばいい。
ユークリッド空間という名前が創られたからには、非ユークリッド空間が発見されたというわけだが …
👆 2本の平行する直線が存在するのが ユークリッド空間だった
地球が丸いことを人類が知ったのは 紀元前のギリシャ人だと思うが、そこからいったん忘れられて、再び地球が丸いことが知られるようになったのは 1500年代のマゼランたちの世界一周旅行だろう
もし地球が真球で、すべて海で覆われていて、2つの船に対して 進んだ航路が交わらないような直線上を2隻で進め、と指示するとする。
すると、どのような航路を選ぼうと2つの船の航路はいつか交わってしまう。球の表面では平行線というものが存在しない
このように平行線が存在しない空間を 非ユークリッド空間 と呼ぶ。
ニュートン法を創ったラフソンやニュートンたちは、まだユークリッド空間を扱う時代の数学者だ
ニュートン法が出てくるのは、まだユークリッド空間と呼ばれていなかった時代のユークリッド空間の、さらにその中の1つの デカルト座標 でだ

デカルト座標が何かというと、これも中学校で出てくるような いつもの座標 だ。
ちなみに おそらくデカルトは デカルト座標 を使っておらず、後世の人が デカルトは偉大な数学者なので名前を残そうとして デカルト座標 という名前にした
デカルト座標 という名前が創られるぐらいだから、デカルト座標じゃない座標も存在する。それが 極座標 (Polar Coordinates)だ

👆 めんどくさいから極座標を雑に描いたが、X軸が円を描いていて、Y軸が中心から外側に向かっている。地球の緯度と、空の高さを表しているとでも思ってほしい
まるで、メルカトル図法と 地球儀のように 地球の表面の地図を作るのに2つの方法があるように、
数学にも デカルト座標と 極座標の2つがあって 利便性が異なるから2つの方法もある
このデカルト座標上の任意の点と、極座標上の任意の点は、少々アバウトながら マッピング(対応付け)することができる。
無限のかなたまで小さな点を完璧に1対1にマッピングできるか?というとできないんじゃないかと思うが、実用的には十分だと思う
この デカルト座標から極座標へのマッピング、または極座標からデカルト座標へのマッピングを可能にするのが、 三角比 とか、三角関数 と呼ばれるものだ。
そして 三角比の中でも 接線(タンジェント) というやつが デカルト座標にも、極座標にも、どちらにも居るおかげで マッピングの橋渡しをしてくれる。接線はすごい
接線
接線とは何か? だが …

👆 例えば 円を描いてみよう
円で有名な数学者に シラクサのアルキメデスがいる。彼は死の直前の最後の言葉として「私の円を壊すな!(Noli turbare circulos meos!」という有名な台詞を残している。 多分 自分も死の直前に「私の円を壊すな!」と言いたい数学ファンとか居ると思う
数学的には 線は太さを持たないので、学校で習う幾何学は 本当は黒板に何も図形が見えないはずなんだが、それだと 勉強ができないんで 数学の先生たちは仕方なく 線を引いているのだと思おう
線に太さが有るのと 無いのとでは 計算結果が変わってくるケースがあり、
そもそも存在しない線の太さを数えて「数学の間違いを見つけた!」とか言う人が出てくるのは ツイッターの風物詩でもある
では次に、円に対して 1本の直線を引いてみよう。
その引き方のうち 重要なのは 3種類あると 2000年間ほどの人類たちは まとめている

👆 1つは接線(タンジェント)。円をかすったような線のことだ。厳密には 円周上の1点だけを通った直線だ。
「隣の点とぶつかるから、1点を通るなんてことはできないのでは?」と考える人がいるかもしれない。その人は「点に大きさがある」と思っている。
線にも、曲線にも、点にも太さは無いのだから、円周上の1点だけを通る直線は引くことができる

👆 2つ目は正割(セカント)。円の表面以外の厚みのある所を貫通したような図だ。厳密には 円周上の2点だけを通った直線だ
中学校では セカントは多分使わないので 三角比の中でも「覚えなくていい」やつ扱いされる。学校とは、その学校と、そのあとの学校の勉強で出てこないものは教えてくれないので、学校に合わなければ落ちこぼれ、学校に合えばめっちゃ勉強ができる人になる。学校の勉強は それ以上でもそれ以下でもない。中には「タンジェントも学校で使わないから要らないのでは?」とかいう人も出てくる。学校では要らないかもしれないが、デカルト座標と極座標をマッピングしたいときには要るのだ

👆 3つ目は円から離れた線だ。厳密には 円周上のどの点も通らない直線だ。これに名前が付いてるのかどうかは知らない
円と三角比の話

👆 円の中心から、円周までの距離を レイディウス (半径;Radius)と呼ぶ
1610年頃までは レイディウスとは 人体の前腕に2つある骨のうち短い方の名前だ

👆 特に レイディウスが 1 である円には名前が付いていて、ユニットサークル (単位円;Unit Circle)と呼ぶ

👆 X軸の1点を固定して持ち上げたときの傾いている具合を アーギュメント(偏角;Argument)と呼ぶ。
その持ち上げ具合を数字で表したものを アングル(角度;Angle)と呼ぶ。
円の1周を360だと決めたものを デグリー(度数法;Degree)と呼ぶ。
円周上を半径と同じ長さだけ進んだ時の角度を 1 と決めたものを ラジアン(弧度法;Radian)と呼ぶ

👆 ここで、極座標でいうと x=30°、y=1 のところにある点Pは、
デカルト座標でいうと xとyはいくつになるだろうか? という変換をしたいことはよくある

👆 そんなときは 思い切って 点Pを通るタンジェントを引く
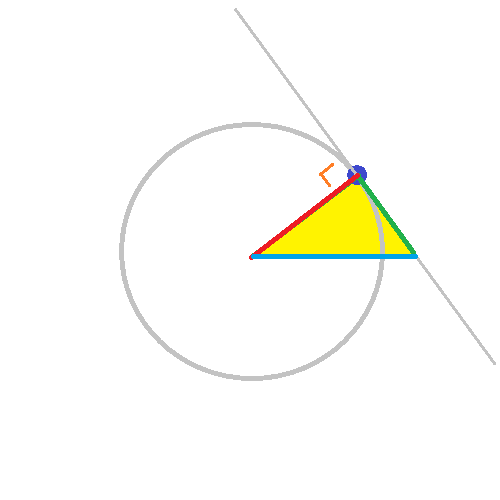
👆 すると 三角形を描ける

👆 三角形を裏返す。
上図の赤線の長さ(底辺)は 1 、
緑色の線の長さ(対辺)は 30°のタンジェント とでも呼ぶとして、
図が描けた

👆 どうにも惜しい。
ただ、点Pと 点Qは 一直線上に並んでいて、
比 にはなってそうだ

👆 ピタゴラスの定理(※)を使うと、原点から点Qまでの ハイパタニュース(斜辺;Hypotenuse)の長さは √(1+t^2) だと分かる
※ピタゴラスの定理 … めんどくさいから、ここでは説明は略

👆 ここで、[原点から点Qまでの長さと比べたときの、原点から点Pまでの長さの割合]、別の言い方をすると[大きな方の三角形と比べたときの、小さな方の三角形の底辺の長さの割合]が分かった。 1/√(1+tan(30°)^2)

👆 また、[原点から点Qまでの長さと比べたときの、点PからX軸への垂線の長さの割合]、別の言い方をすると[大きな方の三角形と比べたときの、小さな方の三角形の対辺の長さの割合]も分かった。 tan(30°)/√(1+tan(30°))

👆 ようやく、点Pのxとyの長さを求める式は分かった
すると「tan(30°) とか √(※ルート)とか どうやって計算するねん?」という問題が残る。
三角比の使い方ではなく、その三角比の数はどうやって求めたのかの方 を知りたいが、インターネットで調べると 使い方の方ばっかり出てくるし、わたしの学力では 三角比の数の求め方 は難しくてよくわかんないので しぶしぶ
三角関数表 や、平方根表 を使って答えを見る、いわゆる テーブル引き をすることになる

👆 これだけ理解して サイン(正弦;sine)と コサイン(余弦;cosine) が出てくる
中学校では サイン、コサイン のついでに タンジェント を暗記することになるが、仕組みを考えると順序は逆で、タンジェントがあるからこそ サインと コサイン にたどり着く
三角比で出てくる12種類の比の話や 平方根の話、三角比の暗記で覚えさせられる √2 とか √3 ってどこから出てきた? などのトピックはまだまだ広げられるが、いったん話を戻す。
ニュートン法で出てくるのは 接線(タンジェント)だ
👆 大げさに言うと、ニュートン(1642~1727、17世紀~18世紀の人物)の活躍した時代の以前と以後で 科学の見方が変わった。
昔の錬金術も 当時は科学だったのだと思うが、そこから 現代人でも科学と思える科学に変えた
そんな時代の人物が ニュートン法の原型を考えて せっせと計算していたと思うと面白い
ここで問題としているのが …

👆 曲線と、円が接しているときだ
曲線と円が接する って何だ? 今度こそ 円周上の2点で接する曲線が出てくるんじゃないの? と思ってしまう
しかし厳密には、円というものは存在しないし、曲線というものも存在しない
曲線に見えてるものは 曲線上に集まった点の並びだし、
円に見えてるものは 円周上に集まった点の並びだ。
点と点を結ぶと 直線になるが、直線に見えてるだけで 点の並びだ。
そして その点は、大きさが無い
かなり難しい。この考えに沿って 大雑把に見てみよう

👆 上図の雑な絵は、曲線上に並ぶ青い点と、円周上に並ぶ赤い点だ
ここで、数学では 接線(タンジェント)と言うように 円周に接した線があると言うが、「点は接しているけど線は接していないじゃないか」とか思う人もいると思う
そこで便利な考え方が 傾き (slope または gradient)だ

👆 点は 傾き を持っている、ということにする
わたしは傾きというと、線にあるものだと思っていたが、
点に傾きがあってもいいのだ
点がどっち向いてるなんか わかんないだろ、と思うかもしれないが、あえて「点にも向きはあるのだ」と思うことにする
関数
`関数` という名前は、プログラミング界隈にも、数学界隈にも出てくる。
歴史的には 数学界隈が先に `関数` を使っていて、
プログラミング界隈が `関数` を自分のところに持ち込んで魔改造した
ここでは 本来の関数の話をする

👆 X軸(X axis)の2を指で押さえたとする

👆 そしたら 必ず もう片方の手の指が Y軸の2を押さえるものとする。
すると、X軸の2と、Y軸の2は 関係がある と考える。
もし X軸のすべての数字と、Y軸のすべての数字に 関係 があれば、
X軸とY軸には 関係がある と考える
とくに X軸のすべての数字と Y軸のすべての数字に関係があるものを
XとYの関数 と呼ぶ。
https://www.kurims.kyoto-u.ac.jp/~kenkyubu/kokai-koza/okamoto.pdf
👆 最初に 関数という概念を考えたのは ゴットフリート・ライプニッツで、
その関数を使い倒して 現代の関数の感じになるまで まとめて整えたのは
ダニエル・ベルヌーイと、 レオンハルト・オイラー なのだそうだ
ライプニッツの 計算機科学への関りの偉大性は すごすぎると思うが
そんなに知られてないの わらう
XとYの関数を数式で表すと `y = f(x)` と書く。
この 丸括弧を使ってX軸の数を囲むことによって 関数ですよ、と分かるようにした書き方は オイラーが流行らせたそうだ
世の中の計算機科学界隈の人の中には「`y = (f)x` にして関数の名前の方を丸で囲ってほしかった。そうしたら `y = f(g(x))` のような入れ子になった関数は `y = (f)(g)x` とフラット書ける。オイラーは2分の1の確率で丸括弧が入れ子になっていく方を選んだ」と思ってる人もいるが、こういう人は主流にはならない

👆 X軸に置いた指の先と、Y軸に置いた指の先に 点を打つ

👆 これを X軸のたくさんの数に対して 関係があるYとの交点に 点を打ったものを プロット(Plot)と呼ぶ
上記は f が y = x だったときのプロットだ

👆 めっちゃたくさんのX軸上の数についてプロットしたものを ライン(線;Line) と呼ぶ
このように、 y = x は直線になる
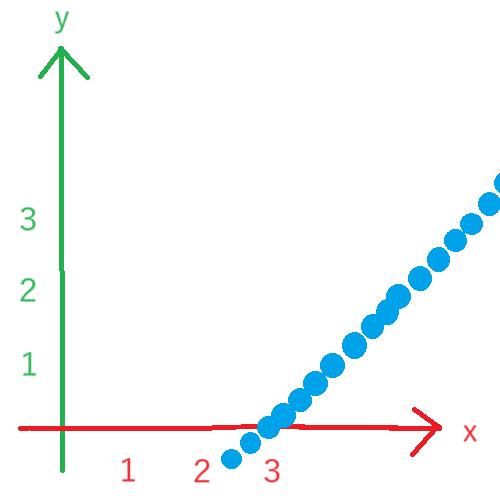
👆 上記のように `y = x - 3` のようにすると、原点を通らない直線を引くことができる。xが3のところで、yが0になっている
ここで、じゃあ 曲線って数式でどう表すの? とかも 絵にしたいところだが 大変なので ここでは飛ばす
y = f(x)
y = f(x)👆 直線にしろ、曲線にしろ、(細かいことは省くがなんか簡単っぽいやつは) `y = f(x)` でイケる
デカルト座標で x がいくつのとき、 y はいくつ、とマッピングしたやつが `y = f(x)` だ。
この y を 0 にしたいとき、
つまり、
数直線 x 上(x軸上)に 点 があるようなときの、x がどこにあるか調べたいときがある。
例えば もし
3 = f(0)だったとする。
そんなときは
0 = f(x) - 3`f(x)` から 3 を引いてやれば、この直線だか曲線だか知らないが関数は、
原点から始まる直線だか曲線に 調整できることが分かる
しかし
4 = f(-1)
y = f( 0)
4 = f( 1)
7 = f( 2)
12 = f( 3)👆 しかし `f(0)` だったときの y をどうやって求めるのか分からない。
そんなときに 漸近(ぜんきん)しながら 求まるよ、というのが ニュートン法
漸近というのは、1発では答えが求まらないけど、2発、3発 と繰り返していけば 答えに近づいていくよ、というものだ
もしいい感じに 漸近すればするほど1つ前よりは1つ後の方が正しい答えに近づくよ、というような 収束 の性質を持っている関数だったら、計算すればするほど 正しい答えに近づいていく。最終的に正しい答えにピッタリたどり着いて動かなくなるか、それとも永遠にピッタリ正しい答えにはならない手前を少しずつ縮んでるかは 知らない
ニュートン法では 接線 を使う
もう少し細かく見ていく

👆 X軸の線上の好きなところを指さすとする。
そこを任意の点(any point) a と呼ぶとしよう
このとき、`f(x)` という式で表される曲線上のうち、 `f(a)` という式で表される点を上図でハイライトした

👆 さらに、点ではなく、点の傾きを表したいときは、`f´(a)`と書くとしよう。 f の字の横に点(プライム)が付いている。
この 点の傾き を求める計算方法を 微分(びぶん) という。
微分の計算方法の説明はどこのWebサイトでもやってるので省略する
f´(a)👆 f の字の横に点(プライム)が付いている

👆 傾きが分かったのだから、その点を通る同じ傾きの線を引いてみる。これが 接線(タンジェント)

👆 `f(a)` の傾きをもった直線と、x軸が交わるところに a2 という任意の点を置くとする。
`y = f(a)` よりは、 `y = f(a2)` の方が、 `0 = f(x)` に近づいていると考える。
同様の操作を繰り返し、
`y = f(a2)` よりは、 `y = f(a3)` の方が、 `0 = f(x)` に近づいていると考える。
これを納得できるところまで繰り返すのが ニュートン法 だ
(書きかけ)
