世界のナベアツのことを考えてた日の話
はじめに
どうも、三重大学大学院二年生のふくぶちょ~(@__DielsAlder__)です。
今回は世界のナベアツがバカになる数、ナベアツ数に関する議論を最近行ったのでそれについて紹介します。
コーディング・実行時間計測・計算量解析なども行っていますが、かなりガバい可能性が高いのでそこらへんは許してくれると幸いです。
また、何もつけずに計算量と言った場合は時間計算量を指すと思ってください。
きっかけ
をくんのポスト
「ナベアツ数を見つけるプログラム、3の倍数はやるだけとして3がつく数は文字列型に変換→1文字ずつ総当たり以外に上手い方法ありますか」
ここから全てが始まりました。
これに対して何人かが手法を提案し、その後議論が広がったためそれを紹介します。
問題の大まかな設定
ある数$${N}$$が与えられた時、$${N}$$の中に3が含まれるか判定を行ってください。
ただし、諸事情(早めに出た考えの中に$${1\dots N-1}$$に関する情報が必要なものがあったため)より次のような問題を解くことにしました。
ある数$${N}$$が与えられた時、$${1\dots N}$$の中に3が含まれる数が何個あるかを数え上げてください。
みんなの考え
をくんの考え
文字列型に変換して1文字ずつ総当たりすれば良いのでは?
int cou=0;
for(int i=1;i<=N;i++)
{
string S=to_string(i);
for(int j=0;j<S.length();j++)
{
if(S[j]=='3'){cou++;break;}
}
}よっしいくんの考え
0になるまで10で割り続けて、どこかのタイミングであまり3が出てくるか見れば良いのでは?
int cou2=0;
for(int i=1;i<=N;i++)
{
int x=i;
while(x!=0){
if(x%10==3){cou2++;break;}
x/=10;
}
}てとらくんの考え
3がどこかに含まれる数の集合をN-1まで持っておいて、Nの末端が3あるいはN/10が集合にあるかを判定すれば良いのでは?
N-1までの集合が必要だから1~Nまで連続判定するとかではないと微妙だけど。
set<int>se;
for(int i=1;i<=N;i++)
{
if(i%10==3||se.find(i/10)!=se.end()){se.insert(i);}
}てとらくんの考え追加実装
てとらくんのやつは平衡二分木の利用が重いのではないか?と思ったので動的配列と素朴な二分探索(競プロで言う「めぐる式二分探索」)で実装。
vector<int>vec;
for(int i=1;i<=N;i++)
{
int div=i/10;
if(i-div*10==3){vec.push_back(i);}
else
{
//vec[l]<i/10,vec[r]>=i/10
int l=-1,r=vec.size(),mid;
while(r-l>1)
{
mid=((l+r))>>1;
if(vec[mid]<div)
{
l=mid;
}else
{
r=mid;
}
}
if(r!=vec.size()&&vec[r]==div){
vec.push_back(i);
}
}
}てとらくん+ふくぶちょ〜の考え
そもそも毎回二分探索しているが、集合のデータは小さい順に参照されるのでカーソルとなる変数を用意してずらせばよいのでは?
int cur=0;
vector<int>vec2;
for(int i=1;i<=N;i++)
{
int div=i/10;
if(i-div*10==3){vec2.push_back(i);}
else
{
while(cur!=vec2.size()&&vec2[cur]<div){cur++;}
if(cur!=vec2.size()&&div==vec2[cur])vec2.push_back(i);
}
}ふくぶちょ〜の考え
1~Nの中の3が含まれた数を考えるという問題設定なら、普通に動的計画法すれば最強なのでは?
上位i桁目まで見たとき、状態jであるような数は何個あるかをdp[i][j]で保有して遷移を行います。
かなり難しいので気になる方は「桁DP」などでググってみるとよいかもしれません。
string T=to_string(N);
//0->Nとぴったり3がない、1->Nとぴったり3はある、2->N未満確定3なし、3->N未満確定3あり
vector<vector<int>>dp(T.size(),vector<int>(4,0));
for (int i = 1; i <= T[0]-'0'; i++)
{
int tmp=0;
if(i==3)tmp++;
if(i!=T[0]-'0')tmp+=2;
dp[0][tmp]++;
}
for (int i = 1; i < T.size(); i++)
{
if(T[i]=='3'){
dp[i][1]=dp[i-1][1]+dp[i-1][0];
}else{
dp[i][0]=dp[i-1][0];
}
dp[i][2]+=9*dp[i-1][2];
dp[i][3]+=dp[i-1][2]+10*dp[i-1][3];
if(T[i]>'3'){
dp[i][2]+=(T[i]-'1')*dp[i-1][0];
dp[i][3]+=dp[i-1][0]+(T[i]-'0')*dp[i-1][1];
}else{
dp[i][2]+=(T[i]-'0')*dp[i-1][0];
dp[i][3]+=(T[i]-'0')*dp[i-1][1];
}
dp[i][2]+=8;
dp[i][3]++;
}Yuくんの考え
反転した文字列を用いてインクリメントを表現し、常に文字列内の3の数を保有し続けることで判定すればよいのでは?
これについては、Yuくん自身がほぼすべて実装しており、不必要な部分を省いたりしたものになります。
int cou4=0;
int res=0;
for(int i=1;i<=N;i++)
{
int j;
for (j = 0; j < R.length(); j++)
{
if(R[j]!='9')break;
}
if(j==R.length()){
R.push_back('1');
}else{
if(R[j]=='3'){
cou4--;
}
R[j]++;
if(R[j]=='3'){
cou4++;
}
}
for (int k = 0; k < j; k++)
{
R[k]='0';
}
if(cou4){res++;}
}本来の視点
本来はある数が与えられた時それに3が含まれているかという視点だったので、それを満たしたをくんとよっしぃくんの考えを尊重すべきと思いました。
そこで、やや速かったよっしぃくんの考えに基づいたプログラムをより速くするためOpenMPで並列化してみました。
ぼくのPCはRyzen 3900Xを搭載しており、スレッド数がやや多いのでこの並列化はかなり効く結果に。
int cou3=0;
#pragma omp parallel for reduction(+:cou3)
for(int i=1;i<=N;i++)
{
int x=i;
while(x!=0){
if(x%10==3){cou3++;break;}
x/=10;
}
}実際に実行して計算時間を見てみよう!
様々なデータサイズで実行してました。
単位は秒です。
$$
\begin{array}{c:c:c:c:c:c:c}
人名\backslash データサイズ&10^4& 10^5 & 10^6 &10^7& 10^8&10^9\\ \hline
を&0.001&0.005&0.052&0.551&5.738&59.676\\
よっしい&0&0.001&0.011&0.116&1.282&13.985\\
よっしい(マルチコア)&0.001&0.001&0.002&0.010&0.116&1.291\\
てとら(\text{set})&0.003&0.027&0.344&4.247&52.886&\times\\
てとら(二分探索)&0&0.005&0.059&0.723&8.424&96.359\\
てとら+ふくぶちょ~&0&0.001&0.011&0.112&1.146&12.515\\
ふくぶちょ~&0&0&0&0&0&0\\
\text{Yu}&0&0.001&0.014&0.138&1.350&13.856
\end{array}
$$
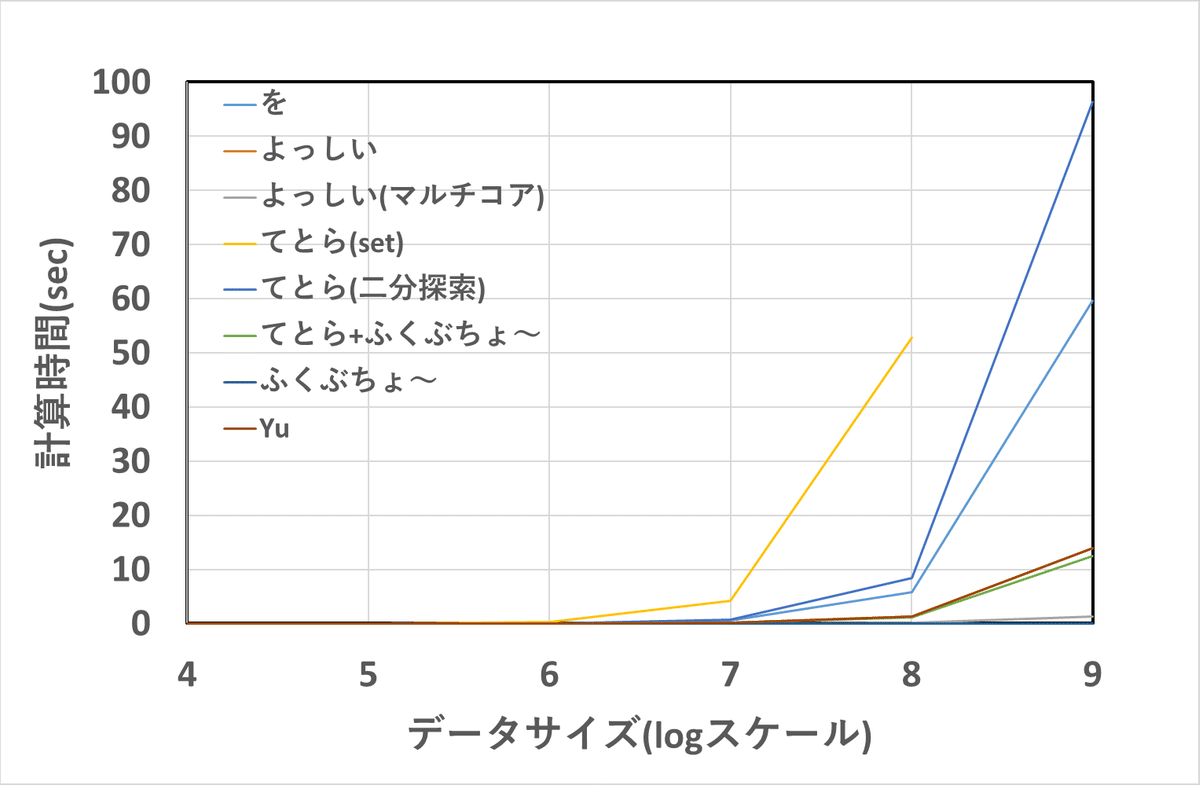

計算量解析
本当だったら四則演算を$${O(1)}$$としたかったのですがこの部分を避けると説明しにくい点もあったため、今回は+と-を$${O(1)}$$、*と/と%を$${O(\log N)}$$として考えました(定数との演算しか基本的にないので、このような計算量としました。STL内部の辺りまでは考慮しきれてないのでそこは許して)。
をくんの考え
ボトルネックは文字列変換部分で多分$${O(\log N)}$$。
そのため$${N}$$まで計算するのに全体$${O(N\log N)}$$かかっています。
やや、文字列変換部分の定数が重いように思われます。
よっしぃくんの考え
ボトルネックは割り算の繰り返し部分です。
割り算回数が$${O(\log N)}$$であり、それが$${O(\log N)}$$回行われるので1つの数字の判定に$${O(\log^2 N)}$$かかってしまうような気がします。
しかし、実行結果を見る限りそこまでかかっているほど遅くは感じません。
これは、桁が多くなるごとに3を含まない数が減っているからです。
より詳しくお話ししましょう。
十分大きな$${n}$$桁のランダムな数を考えます。
下$${1}$$桁目で初めて3が現れる確率は$${\frac{1}{10}}$$
下$${2}$$桁目で初めて3が現れる確率は$${\frac{1}{10}\times \left(\frac{9}{10}\right)^1}$$
下$${3}$$桁目で初めて3が現れる確率は$${\frac{1}{10}\times \left(\frac{9}{10}\right)^2}$$
……
下$${n}$$桁目で初めて3が現れる確率は$${\frac{1}{9}\times \left(\frac{9}{10}\right)^{n-1}}$$
下$${n}$$桁目は先頭の桁なので0を含まないことに注意。
3が現れない確率は
$$
1-\frac{1}{10}\left(\sum_{k=1}^{n-1}\left(\frac{9}{10}\right)^{k-1}\right)-\frac{1}{9}\times \left(\frac{9}{10}\right)^{n-1}=\left(\frac{9}{10}\right)^{n-1}-\frac{1}{9}\times \left(\frac{9}{10}\right)^{n-1}=\frac{8}{9}\times \left(\frac{9}{10}\right)^{n-1}
$$
3が現れない場合は簡単のため$${n+1}$$桁目に3があるとして考えることにします。
3が出現する場所の期待値は
$$
\frac{1}{10}\left(\sum_{k=1}^{n-1}k\left(\frac{9}{10}\right)^{k-1}\right)+\frac{n}{9}\times \left(\frac{9}{10}\right)^{n-1}+\frac{8(n+1)}{9}\times \left(\frac{9}{10}\right)^{n-1}
$$
$${n}$$を無限に近づけていくと2項目以降は$${0}$$に収束し、1項目は高校数学の数列でやった手法で、等差数列と等比数列の積の和を計算すると(俺は面倒なのでWolfram Alphaを使いました)$${10}$$になります。
即ち、これは定数で抑えることができ、割り算回数はならし$${O(1)}$$と言えます。
結論としてはこれも1回の数の判定に$${O(\log N)}$$かかり、全体で$${O(N\log N)}$$となります。
てとらくんの考え
割り算が$${O(\log N)}$$であること+集合に含まれる数が$${O(N)}$$で抑えられることから、1回の判定にかかる計算は$${O(\log N)}$$となり、全体では$${O(N\log N)}$$。
てとらくん+ふくぶちょ〜の考え
割り算がボトルネックであるため結局1回の判定に$${O(\log N)}$$かかり、全体で$${O(N\log N)}$$となるが、やや重い二分探索部分がないためかなり高速。
ふくぶちょ~の考え
$${O(\log N)}$$かかる四則演算が$${O(\log N)}$$回行われるから、合計$${O(\log^2 N)}$$であり、ぶっ壊れてるくらい速い。
Yuの考え
文字列でインクリメントを実装しています。
乗算や除算がないので$${O(1)}$$でうれしいですが、繰り上がり回数について考える必要があります。
繰り上がり回数は各桁に着目すると、1の位は10回に1回、10の位は100回に1回……となっており無限等比級数から定数に収束します。
そのためこれは正しく1回の判定にならし$${O(1)}$$で全体$${O(N)}$$となります。
まとめ
今まで出てきたものをまとめてみましょう。
表に出てくるワードは以下のように定めます。
単体の計算量は1つの数$${N}$$に3が含まれるか判定するのにかかる計算量。
全体の計算量は$${1}$$から$${N}$$に3が含まれる数が何個あるかを計算するのにかかる計算量。
列挙可能は$${1}$$から$${N}$$に3が含まれる数が何個あるかを計算したときに個数だけでなく具体的にそのような数を列挙可能か。
$$
\begin{array}{c:c:c:c}
人名&単体の計算量 & 全体の計算量 & 列挙可能 \\ \hline
を&O(\log N)&O(N\log N)&\circ\\
よっしい&O(\log N)&O(N\log N)&\circ\\
てとら&O(N\log N)&O(N\log N)&\circ\\
てとら+ふくぶちょ~&O(N\log N)&O(N\log N)&\circ\\
ふくぶちょ~&O(\log ^2 N)&O(\log ^2 N)&\times\\
\text{Yu}&O(N)&O(N)&\circ
\end{array}
$$
おまけ
全員分のコードを載せておきます。
#include <time.h>
#include <iomanip>
#include <iostream>
#include <set>
#include <string>
#include <vector>
#include <omp.h>
using namespace std;
int main() {
cout << fixed << setprecision(3);
//入力
int N;
cin>>N;
cout<<"datasize = "<<N<<endl;
//をくんのシステム(文字列に変換して'3'を見つける)
auto s=clock();
int cou=0;
for(int i=1;i<=N;i++)
{
string S=to_string(i);
for(int j=0;j<S.length();j++)
{
if(S[j]=='3'){cou++;break;}
}
}
auto t=clock();
cout<<"Wo system"<<endl;
cout<<"result = "<<cou<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
//氷凝りくんのシステム(0になるまで10で割り、あまり3を見つける)
s=clock();
int cou2=0;
for(int i=1;i<=N;i++)
{
int x=i;
while(x!=0){
if(x%10==3){cou2++;break;}
x/=10;
}
}
t=clock();
cout<<"Hikori system"<<endl;
cout<<"result = "<<cou2<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
//氷凝りくんのシステムをOpenMPで高速化
s=clock();
int cou3=0;
#pragma omp parallel for reduction(+:cou3)
for(int i=1;i<=N;i++)
{
int x=i;
while(x!=0){
if(x%10==3){cou3++;break;}
x/=10;
}
}
t=clock();
cout<<"Multicore Hikori system"<<endl;
cout<<"result = "<<cou3<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
//テトラくんのシステム(setでN未満を持つことでN/10がsetに含まれるかと末尾の数字を見て判断)
/*
s=clock();
set<int>se;
for(int i=1;i<=N;i++)
{
if(i%10==3||se.find(i/10)!=se.end()){se.insert(i);}
}
t=clock();
cout<<"Tetra system"<<endl;
cout<<"result = "<<se.size()<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
*/
//テトラ君のシステムをsetではなくvectorと二分探索で実行
s=clock();
vector<int>vec;
for(int i=1;i<=N;i++)
{
int div=i/10;
if(i-div*10==3){vec.push_back(i);}
else
{
//vec[l]<i/10,vec[r]>=i/10
int l=-1,r=vec.size(),mid;
while(r-l>1)
{
mid=((l+r))>>1;
if(vec[mid]<div)
{
l=mid;
}else
{
r=mid;
}
}
if(r!=vec.size()&&vec[r]==div){
vec.push_back(i);
}
}
}
t=clock();
cout<<"Tetra system2"<<endl;
cout<<"result = "<<vec.size()<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
//テトラ君のシステムを現在の数字の1/10以上ギリギリの配列の位置を保持し続ける変数を利用して実行
s=clock();
int cur=0;
vector<int>vec2;
for(int i=1;i<=N;i++)
{
int div=i/10;
if(i-div*10==3){vec2.push_back(i);}
else
{
while(cur!=vec2.size()&&vec2[cur]<div){cur++;}
if(cur!=vec2.size()&&div==vec2[cur])vec2.push_back(i);
}
}
t=clock();
cout<<"Tetra Fukubutyo system"<<endl;
cout<<"result = "<<vec2.size()<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
//チート(上位i桁まで見た時の答えを動的計画法で計算)
s=clock();
string T=to_string(N);
//0->Nとぴったり3がない、1->Nとぴったり3はある、2->N未満確定3なし、3->N未満確定3あり
vector<vector<int>>dp(T.size(),vector<int>(4,0));
for (int i = 1; i <= T[0]-'0'; i++)
{
int tmp=0;
if(i==3)tmp++;
if(i!=T[0]-'0')tmp+=2;
dp[0][tmp]++;
}
for (int i = 1; i < T.size(); i++)
{
if(T[i]=='3'){
dp[i][1]=dp[i-1][1]+dp[i-1][0];
}else{
dp[i][0]=dp[i-1][0];
}
dp[i][2]+=9*dp[i-1][2];
dp[i][3]+=dp[i-1][2]+10*dp[i-1][3];
if(T[i]>'3'){
dp[i][2]+=(T[i]-'1')*dp[i-1][0];
dp[i][3]+=dp[i-1][0]+(T[i]-'0')*dp[i-1][1];
}else{
dp[i][2]+=(T[i]-'0')*dp[i-1][0];
dp[i][3]+=(T[i]-'0')*dp[i-1][1];
}
dp[i][2]+=8;
dp[i][3]++;
}
t=clock();
cout<<"Cheat system"<<endl;
cout<<"result = "<<dp[T.size()-1][1]+dp[T.size()-1][3]<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
s=clock();
string R="0";
int cou4=0;
int res=0;
for(int i=1;i<=N;i++)
{
int j;
for (j = 0; j < R.length(); j++)
{
if(R[j]!='9')break;
}
if(j==R.length()){
R.push_back('1');
}else{
if(R[j]=='3'){
cou4--;
}
R[j]++;
if(R[j]=='3'){
cou4++;
}
}
for (int k = 0; k < j; k++)
{
R[k]='0';
}
if(cou4){res++;}
}
t=clock();
cout<<"Yu system"<<endl;
cout<<"result = "<<res<<endl;
cout<<"time : "<<(double)(t-s)/CLOCKS_PER_SEC<<" sec"<<endl<<endl;
}
最後に
みんなのプログラムを実際に実装して検証するの楽しかったです。
