『スタ演』の正しい使い方
こんばんは、家庭教師のせむです。
増刊号紹介シリーズとして、今回は増刊号の中でおそらくもっともメジャーな問題集『新数学スタンダード演習』および『数学Ⅲスタンダード演習』(以下、スタ演)を解説します。
下の方に、入試数学問題の難易度構造と、それに基づいて「スタ演にどのように取り組めばよいか?」といったアドバイスも記しています。
このくらいのレベルの問題集を解く際、「問題の解法だけでなく背景や『なぜそうなるか』までしっかり理解しなさい」とはよく言われることですが、個人的には背景の理解よりも重要な観点があると思っています。
スタ演に限らず、『プラチカ』や『やさ理』、『上問』、『入試の核心』など、似たような難易度の問題集を扱う際に全般的に言えるアドバイスです。よければ最後まで読んでみてください。
内容
問題数と難易度
画像でまとめました。
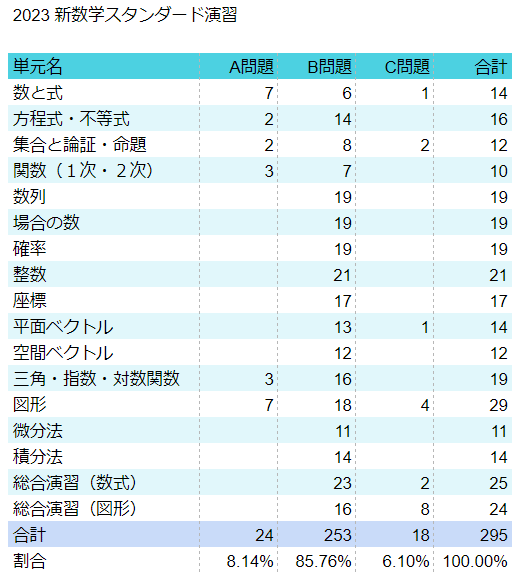

問題難易度は大数基準のB問題がメインです。一部AやCも混じっています。
B問題は完璧にすれば一部医学部以外どこでも受かります。例えば東大理系は6問セットでBBCCCCくらいが標準的な難易度で、B完答&C部分点でボーダーは余裕で超えます。
前提学習
一通りのインプットが終わっている人が対象です。
チャートエクササイズまで、またはチャート例題+練習+1対1or標問。
記述模試は(文理の差はありますが)ざっくり150点前後くらいを取れる学力がほしいです。(偏差値65〜70)
解説
だいぶ簡素ですが、インプットがしっかり済んでいるなら特に困らないレベルです。逆に、この解説が読めないのならチャート修行が足りません。
ちなみに解説は簡素ではありますが、決して不足しているわけではありません。他の同レベルの問題集はやたら詳しくアレコレ言ってきますが、個人的にはこのくらい簡素な解説でパパッと答え合わせ&見直しをしたい派です。
到達度
諸説ある部分です。
1〜2周解いて、不明点をあらかた解決し、問題を見たら大体の方針が分かる、という状態になったとしても、その時の学力(実力)は、人によって大きく異なります。
実力の下限では、地方国公立の合格者平均くらいにしか仕上がらないです。旧帝大数学で3割〜4割くらいしか取れません。逆に上限の人は、例えば東大志望の場合、この後の過去問演習で、しょっぱなから文系65点〜満点、理系65〜85点くらいが狙えます。
このあたりの差がなぜ生じるかについて、下の方で詳しく考察しています。
スタ演の次
一般的には過去問へ行きます。
時期と志望校によっては、さらに難しい問題集へ進みます。
僕は公立高校の生徒の指導がメインですから、時期的にそこまでやる余裕がある子はいません。中高一貫なら余裕ありそう。
次の問題集ですが、一般的にはC問題~D問題を扱う「新数演」などの難しい問題集へと進むとされていますが、B問題オンリーのスタ演とC問題ばかりの新数演との間には結構な難易度のギャップがあり、いきなり突撃するとボッコボコにされます。また、新数演も250問くらいの収録数があるため、本当に余裕がないと手が出しづらい問題集でもあります。
そこで僕は、スタ演の次に過去問以外の問題集に取り組むのであれば、月刊大数の12月号~2月号をおすすめします。
この号は総合演習の号で、スタ演の最後の単元みたいな問題が並びます。
難易度・問題数は以下の通り。

ⅠAⅡBの問題も、全体的に理系入試からの出題が多いです
なので「理系数学」としての割合は相当大きいです
ちょうどよくないですか?スタ演からの接続が抜群に良いのが難易度比率からも明らかです。
数Ⅲ演習がC問題ばかりで難しそうに見えますが、これは計算が重たい大問が多いだけです(平均して大問1つ30分くらい)。それぞれ小問3つ~4つくらいで構成された問題が多く、完答までの道のりは一本道に整備されているため、大元の発想として高度なものはそう多くありません。
これを全部やるのに最短1.5ヶ月(1日3題)、最長5ヶ月(1日1題)、平均的な想定2.5ヶ月(1日2題)です。新数演は最短2.5ヶ月、最長半年以上、平均想定5ヶ月くらいが想定されますし、難易度的にもオーバーワークな場合が多いですので、月刊大数の総合演習号を解く方が丁度良いはずです。
理系からすると数Ⅲの問題数がやや少ないように感じられるかもしれませんが、そちらは代わりに過去問演習で多く扱うはずですので、バランスは取れます。ⅠAⅡ演習などは切ってもいいですし、「微積分・基礎の極意」など数Ⅲ特化の問題集で補っても良いでしょう。
旧版との比較(易化した?)
スタ演は旧版(2014年くらいまでのもの?)と現行版とで、内容が大きく異なります。
2014年くらいまでは改定もあまり行われておらず、2000年前後の入試問題しか収録されていません。
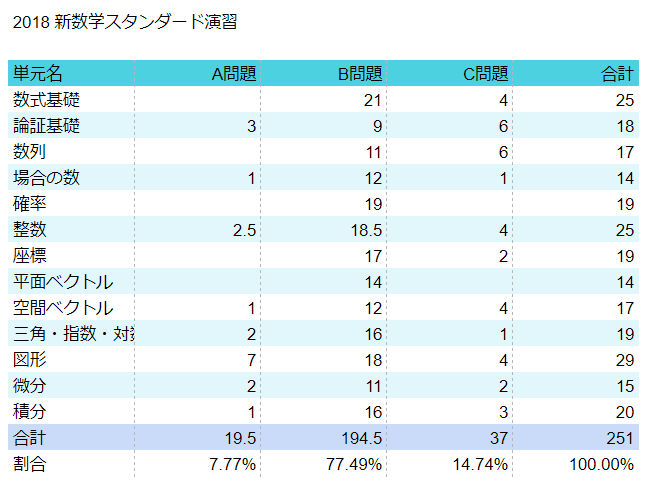

まあ見ての通り、C問題の割合は旧版の方がやや多いです。
だからといって、難しい旧版の方が優れているというわけではありません。個人的には現行版の方が、学習効果はより高いと感じています。
現行版は1対1や標問などからの接続が良く、順を追ってやってきた子に効く難易度に仕上がっています。
また、昔の入試問題は発想力重視の問題が多く、旧スタ演には「そんなの初見で思いつかねーよ!」という問題が少なからず収録されています。大数難易度はおもに「解法や発想の高度さ」で難易度分けしているため、どうしても旧スタ演の方が平均難易度が高く出がちになります。
一方、現代のスタ演は、地道で正確な計算を積み上げていく能力が要求されていると感じます。新版スタ演には分野混合の総合演習が計50問ほど追加されています。同じB問題でも単元別演習より重たく感じられるものばかりですので、実際の難易度でそこまで劣っているとも感じません。問題数は現行版の方が多いので、最終的にやり抜く労力は大差ないと考えています。
総合的に言えば、難易度表記上は旧スタ演の方が難しく見えますが、1対1やチャートなどからの接続の良さを踏まえれば、学習効果などで現行スタ演に軍配が上がります。
そもそも発想力を鍛えたかったら、もっと難しい問題集で鍛えれば良いだけなので、中途半端にスタ演の難しい版を使う意味は…。
本題:非典型問題との向き合い方
先程、「到達度は人によって大きく異なる」と延べました。
思うように伸びない子たちの解き方が悪いわけでも、雑なわけでもありません。「なぜそうなるのか」までしっかり押さえた受験生の間でも、得点力には結構大きな差がつきます。
これを「数学が得意だから/苦手だから」という才能的な話で一括りにしてしまっては進展がありませんので、今回はこれを「問題との向き合い方」という観点で考察してみます。
この差の原因ですが、僕の考察では、「非典型問題との向き合い方が違うから」という風に結論付けることができます。
非典型問題というのは、「難関入試っぽい問題」のことです。1問1問がユニークで、少なくとも見た目は初見の問題になります。当然、教科書(および教科書の近傍延長線上にある問題集)に載っているはずがない問題でもあります。
向き合い方の要点は、大きく分けて2つあります。「問題を典型問題に分解すること」と、「完答する上でのヤマ場を見極めること」の2つです。
典型問題への分解
問題がどれだけ非典型か(つまり、どれだけ思考力を要するか)というのは、「問題を試験場で完答できる人数」と「問題の解説を読んで理解できる人数」の差の大きさに現れます。
偏差値55くらいあれば、東大数学の解答は誰でも読めます。実際、答えを読んで「なんだ、東大もこの程度か」と思ったことがある人も少なく無いはずです。
一方、合格ボーダーや合格者平均は5.5割~7割くらいのところにありますから、偏差値70の受験者集団であっても、本番では半分取れれば合格が十分に見える点数になります。
数学の問題は、積み木に例えることができます。解答の微小ステップをそれぞれ小さな典型問題に分解することによって、解答実績を積み上げていくのです。それを一定の高さまで積み上げたら完答になります。
難関大の難しさは、初見の問題しか出ないせいで、「積み上げるべき積み木(=分解された典型問題)がどのような形で、どのような大きさなのか」を判断するのが難しいということです。
問題のヤマ場・3種類
「ここまでは絶対に合っているはずなのに、ここから先に進めない……」という経験はありませんか?
これは難関大入試に限らず、数学あるあるの現象です。その理由は、問題のヤマ場に対する解像度が低いためです。
解きはじめから完答するまで、問題難易度は一定ではありませんし、一定の割合で難易度が上昇し続けるわけでもありません。ある時突然難しい瞬間が来ます。このヤマ場を超えられるかどうかで、合格点までの距離が大きく変わってきます。
体感では、B問題は完答するまでに1~2箇所、C問題は2~3箇所のヤマ場があります。
正答率が明確化されている共通テストで、問題内部の難易度推移とヤマ場の位置を確かめてみましょう。

「カ」と「キクケコサ」の間に大きめの正答率の溝があり、「キクケコサ」が解けた子の多くが「シ」と「ス」も解けたことが予想されます。
つまり、「キクケコサ」で行き詰まった受験生と、その先に進めた受験生には、合計9点の差が付いていることが予想されます。
これが第一のヤマ場で、「負けるかどうか」のヤマ場です。ここを超えられなければ勝負の土俵に立てませんので、負けが確定します。
第一のヤマ場は、基礎~標準の問題をしっかり自分のものにできているかどうかで差がつく部分です。問題難易度はそれぞれですが、この問題ならば、チャート基本例題の解法が淀みなく出てくる人は、ここを乗り越え、勝負の土俵に立てた、と考えて良いでしょう。
また、「ス」と「セソタチツテトナニヌネノ」の間に隔絶的な得点率の差があります。
共テの最終問は捨てる戦略でやっている受験生も多いでしょうから、ここは一概に語るのは難しいかもしれませんが、共テ数学の満点付近で勝負することになる難関大志望の受験生にとって、「セソタチツテトナニヌネノ」のヤマ場を超える力があるかどうかは、一つの差になるはずです。
これが第2のヤマ場で、「勝てるかどうか」のヤマ場です。第1のヤマ場を超えて勝負の土俵に上がった受験生たちの中で差をつけるのか・つけられるのかは、「セソタチツテトナニヌネノ」を解答できたかどうかにかかっていると言えます。
問題の後半に訪れるヤマ場は、前問の誘導にしっかり乗れたかどうか?という点や、問題の全体像を把握できているかどうかがカギです。このあたりを意識するクセがついているかどうかで、乗り越えるべき壁の高さが大きく変わってきます。

問題の初っ端に一番デカいヤマ場が来てしまうパターン、つまり初手ゲーの問題です。第1のヤマ場と第2のヤマ場が来て、「勝者だけいきなり決まる」パターンと言えなくもないですが、私はこれを第3のヤマ場に分類しています。
手が出せるかどうかでそもそも大きな差が生じてしまい、合格者以外は白紙であることが珍しくない問題です。
これは、日頃からどれだけ丁寧に問題を解いてきたかが分かれ目になるところです。すぐに諦めて答えを見てしまう悪癖がある子にはなかなか難しいです。こういう正答率分布の問題では、試行錯誤の上手さや状況把握の上手さが問われます。実験をしてみたり、状況を図に表したり、問題文の意味と数式を相互に行き来して考えたりといったことを日頃からやっているかどうかが、この問題を征する分かれ目になります。
スタ演を使う際には
上記の話を踏まえれば、スタ演の問題とどのように向き合えばよいか、もう自明のはずです。
すなわち、
・一捻り加えられた問題を、既知の典型問題に分解する力
・問題のヤマ場を乗り越える力
という2点が、スタ演で養うべき力であり、常に意識しなければいけない力です。
特にヤマ場を乗り越える力は重要です。
上記の正答率分析は、上から下まで幅広く受ける共通テストの数字です。勝負の本番である2次試験は似たような学力層の受験生が集まりますし、レベルの高い受験生ほど丁寧で網羅度の高い学習をしていますから、「ここまでは確実に解ける。ここから先は難しい」がよりはっきりします。また、小問の多い共テと異なり、2次試験の大問は小問が無かったり、小問1つあたりの解答量が多かったり等、共テよりももっと過酷な解答環境になります。
つまり、ヤマ場の前後での正答率の差はもっと大きく開くことが予想されます。
この2つの力を養えたならば、東大数学で合格者平均以上が狙えるようになります。1週終えただけでも、過去問で5割~6割くらいは余裕で狙えるでしょう。逆に全く養えなければ、いつまで経っても3割~4割がせいぜいだと思われます。
スタ演→過去問だけで合格点を取る子と、スタ演→新数演(C問題を中心に収録した、スタ演よりもうワンランク難しい問題集)→過去問で合格点を取る子で、勉強量が違うのに入試得点が同じなのは、究極的には上記のような構造を押さえた上での学習ができているかどうか、の違いだと思われます。
難しさの構造を理解していないと、曖昧な学習しかできません。
ちなみに、他の同レベルの問題集を扱う場合でも、この観点は同様に大切です。
一般的にプラチカやスタ演は「アウトプット教材」に分類されますが、世の中でよく言われている「なぜそうなるかまで理解すること」ってやつ、これ結局やってることはインプットじゃないですか??真のアウトプットは、大問を解ききるまでの流れや立ち回りを身につけることにあると考えるべきです。
この記事が気に入ったらサポートをしてみませんか?
