へやわけをグラフとして扱う際の考え方と、へやわけにおける川のグラフとしての位置付け・扱い方

2023年12月17日 15:11

この記事はペンシルパズル Advent Calendar 2023十八日目の記事です
　パズスクに投稿した問題でナンバーリンクの作り方を書くとか言っていましたがテーマ被りで枠も残っていないので今年は書きません。中～大サイズをどうやってきれい目な配置対称で作りつつ作意の複雑な線も成立させるか、という感じのつもりでした。来年あたり書くかもしれない。

0. 前提知識について

　この解説は最低限まり餡氏(X:@agonomy)による、リンク先のペナルティの考え方をある程度理解出来ていること、ペナルティを利用してある程度へやわけが解けることが前提となります。ペナルティの話については知っていないと読みにくいかも。角に黒マスを置くと2辺得、辺に黒マスを置くと1辺得、くらいのイメージがあれば足りている気もする。ただし、私自身がペナルティ理論で解くというより後述のグラフ辺と頂点とループ数の関係式しか使わないで解いているので知っていても読みにくい可能性はあります。
　記事の中で「有効辺」という言葉を多用しますのでどういう意味なのか以下の概要は把握しておいてください。有効辺というのは盤面の孤立した頂点を減らすために有効に使えている辺、くらいの意味です。ループ形成に使われた辺はそのうち一本がなくても頂点が連結しているので無意味、または、注目している領域の頂点同士の接続に辺が使われなければ無意味、という考えから。ペナルティへやわけでは限られた辺の本数で全ての頂点を接続することを目指すことを考えるのでこういう用語があると説明しやすい。

　また、川の話についてはSP1氏の以下の記事
【へやわけ】川の渡り方その1・基本理論編
を理解できていることが前提となります。

1.使用する式や考え方について

1.1.使用する変数の定義について

　上記のペナルティ理論では盤面のへやなど、想定した領域(グラフ)での辺と頂点の数が固定されていました。この記事の内容では盤面の切り抜き方・グラフとしての捉え方によって辺と頂点の数が変わってくるので扱いやすいように式変形します。以下はそこに至るまでの過程と設定した値の意味を書いています。
　まず、まり餡氏のペナルティ解説内容のうち、Xを角にある黒マスの数ではなく、「想定した盤面状態で接続しているグラフ辺の数=2 となる頂点(マス)」、と言い換えます。同様に、Y,Zをそれぞれ「想定した盤面状態で接続しているグラフ辺の数=3 ,4となる頂点(マス)」、と言い換えます。この解説では頂点がマス以外になる場面や、盤面の内側にあっても接している辺の数が4でない扱いのマスなどがあります。とはいえ一瞬おまけみたいな話をするだけですが。上記のペナルティ解説記事では正方形のマスでへやの形状も長方形となるへやわけのみを扱っていたため、接しているマスの数が2なら角、3なら辺、となりましたが、盤面が不定形となったり特殊な状況を考えるときにはその関係が成立しない場合があるので、ちょっとわかりにくいかもしれませんが言い換えをしています。
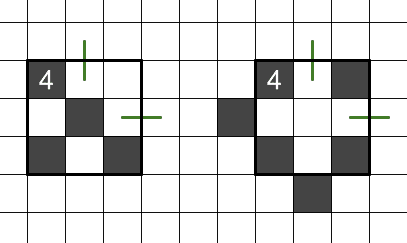
以下にその他各変数の定義を記載します。図も参考にしてください。
(黒マス配置前の注目している領域内のグラフの頂点の数)= v_b
→ペナルティ計算対象となるへやのマス数に相当
(完成盤面のグラフ全体の頂点の数) =v_a
→完成盤面の頂点数(≠白マス残数)に相当
(完成盤面で注目している範囲外の頂点の数 = v_out
→完成盤面においてペナルティ計算対象となるへやの外にある頂点数に相当
(黒マス配置前のグラフ辺の数)= e_b
→ペナルティ計算対象となるへやの初期状態での辺の本数に相当
(完成盤面のグラフ辺の数) =e_a
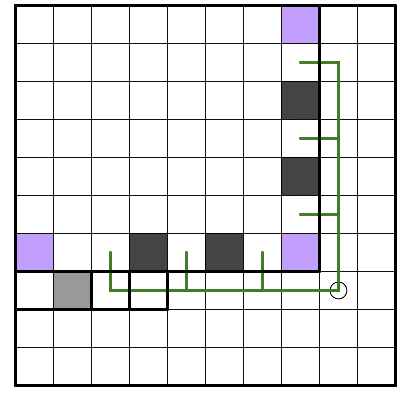
→図の左上で○を結ぶ緑線赤線の合計数
(完成盤面で注目している範囲外の頂点と繋がっている辺の数) = e_out　
(完成盤面で注目している範囲内のループ数) = c_in
(完成盤面で注目している範囲外を含むループ数) = c_out

変数と実際の盤面の対応2
この例では外部頂点を一つと捉えているので右側白マスの形成するループはカウントしない

1.2. 一つのへやとその外部として見た定式化

辺と頂点とループ数の関係式を完成盤面について書くと
e_a = v_a -1 + c
⇒ e_b - 2X - 3Y - 4Z + e_out = (v_b - N + v_out ) -1 + c
(黒マスの数)= N = X + Y +Z　から Z = N - X - Y となるので
3N + v_b - e_b - 1 = 2X + Y - c + e_out - v_out ①
または
3N + v_b - e_b - 2X - Y + c_in = - c_out + e_out - v_out + 1 ②
①式は左辺が初期盤面で確定する定数で、右辺が盤面の埋め方次第の変数となります。右辺を最大化することで表出数字Nがある大きい値でも等式が成り立つ、という形で最大値を考える時に使います。
②はe_a = v_a -1 + c を注目している範囲内と範囲外で左辺と右辺に分けた形になります。後で例を出しますがこの式の左辺が範囲内における非連結成分の数になります。(へやが何個の白マス領域に分割されているか、という値)
※c_outのうち、純粋な領域外のループc_outと、領域内外にまたがったループc_ioは本来分けるべきですが、式の単純化のため領域外のループは一旦ないものとして無視します。あったとしても後々わかるように有効辺の減算を考えてやればよいだけのことなのでそこまで重要ではありません。
②式について、左辺 = v_inとしてやると
e_out = (v_in + v_ out) - 1 + c_out ③
となり、これは盤面全体のグラフにおける頂点と辺とループの関係式そのものとなります。よって v_in は、盤面全体のうち注目している領域(ペナルティ計算対称のへやと思えばよい)を「頂点のみがいくつか入ったブラックボックス領域」として見た時の頂点数を表していることが分かります。

上記の場合、
3N + v_b - e_b - 2X - Y + c_in
=15 + 9 - 12 - 2 * 4 - 0 + 0
= 4
がへやの非連結成分の数です
　以下の部屋のようにその部屋のみでは解が確定しない部屋の場合、本来はへや内にペナルティがあればその分だけ頂点が増えて外部辺の必要数も同じだけ増えますが、それについては後から調整してやれるので今は一旦ペナルティを最小化した黒マス配置での例を書いておきます。

1.3.複数のへやとそれ以外の盤面全体として見た定式化

　ペナルティを計算したい複数の部屋があって、その外部が白マスによってつながっている状況を考えます。以下の図のように灰色部分に記入される現時点では不明な白マスによって各部屋の白マスがつながっているようなイメージになります。

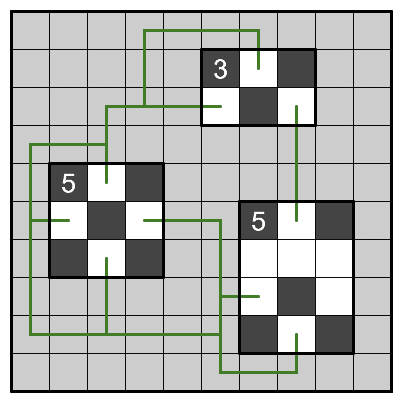
灰色部分の埋まり方は不明だが、何かしら白マスで全体がつながっている状態のイメージ

　注目したいへやが複数あってまとめて扱う場合は、
e_out = Σv_in + v_out - 1 + c_out ④
e_out 、v_out、c_outを部屋の数だけ①式のように分解して整理した形です。
Σv_inは②式の左辺をそれぞれのへやについて計算して足し合わたものですが、v_inは要するに非連結成分数ということが分かっているので、確定した盤面であれば細かい計算をしなくとも求めることができます。上の図でへやの黒マスが確定している場合、上のへやから順に非連結成分数を足すと
Σv_in = 3 + 4 + 2 = 9
　本来v_inは定数ではなくX、Y、c_inを含む変数なので、v_inを定数と変数に分けることを考えます。各部屋について、外部を無視して黒マスを適当に配置した任意の基準状態での非連結成分数をv_in_def、実際の盤面におけるへやのペナルティと基準状態とを比較したペナルティ差をp_diffとして
v_in = v_in_def + p_diff
④にこれを代入して
e_out = Σ(v_in_def + p_diff) + v_out - 1 + c_out ⑤
また、e_1, e_2を
e_2 - v_out = 0 、e_1 + e_2 = e_ out
を満たす数とすると（※意味は後述）、⑤式は
Σ(v_in_def + p_diff) - 1 = e_1 - c_out ⑥
あるいは
Σv_in_def = e_1 - c_out - Σp_diff + 1 ⑦
今後本記事では基本的にはこの⑦式で問題を解きます。
⑦式で基準状態における外部有効辺の本数をe_valid_def、実際の盤面における有効辺の本数との差をe_diffとしてやれば
e_1 - c_out = e_valid_def + e_diff
Σv_in_def = e_valid_def + e_diff - Σp_diff + 1 ⑧
⑥の右辺は注目している領域外の有効辺の数にあたり、「部屋の外に後何本の辺があれば各部屋の白マスを外部領域を使って全て接続できるか」という値になります。後で出す問題でもわかると思いますが⑦あたりの形式が見やすいです。⑧までいくとむしろわかりにくいこともあるので、盤面に応じて計算しやすい式で考えます。
　基準との比較ではなく正確な値を出して普通に解きたい場合は、
v_in = 3N + v_b - e_b - 2X - Y + c_in　から、
3N + v_b - e_b = v_in_def + 2X_def + 2Y_def - c_in_def ⑨
を使えばよいです。この計算結果では、黒マスを全て外周以外のマスに置けた場合の頂点数（非連結成分数）がわかります。
3N + v_b - e_b = (v_b - N) - (e_b - 4N)であることを思い出すと計算結果が頂点数になることがわかりやすい。（黒マスを置いた後に残る頂点数) - (黒マスを置いた後の残りの辺でつなげる頂点の数) = (残りの頂点数) です。この値から1引いた値が、角辺に黒マスを置いたり外部辺を確保したりで稼ぐ必要のある有効辺の数です。
　この、とりあえずv_in_defの状態を作る、つまり適当に黒マスを置いて数えるやり方は、モノを1つずつ指折り数えるより2つ単位で数えると速いという工夫と同じで、黒マス1個で辺4本をまとめて数えられる上に普通のやり方と違って掛け算も桁数の大きい引き算もしなくてよいから速いというだけです。数えるのが部屋の縦横サイズか置いた黒マス数と部屋の分割数になるかだけの違いなら速くて計算も楽な方がいいでしょう。ズルいとか引きみたいだとか思うほどのことではないと思っています。また、特殊形状盤面にも強いです。ちなみに特殊形状盤面だと以下のような黒マスは有効辺2本得ではなく3本得なので、2X、Yの他に3Wの項が式に入ります。(式①、②も同様)

　余談ですが、マス形状が長方形ではなく、1つのマスに接しているマス数が4ではない特殊なマス形状の盤面で同じようにペナルティの式を導出をすると、Nの係数が(中空のマスが接する別のマスの数-1)になり、得する辺の数のパターンだけW, X, Yにあたる項の数が変わります。当然その係数は得する有効辺の本数。式の字面だけ追うより意味を考えた方が式が理解しやすくて自分で係数導出もできるので覚えやすくなると思います。まぁ普通の暗記でも当たり前に使うテクニックではありますが。

Nの係数が2で2XとYの項までになるへやわけ盤面
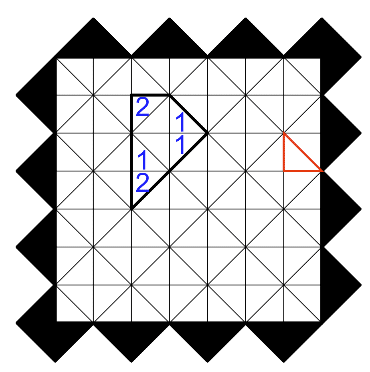
青数字はその部屋でそこに黒マスを置いて得する有効辺の数

※式⑥あたりから現れるe_1、e_2とは何か補足
外部辺の数e_outのうち、v_outをひとつながりにするために使われてv_inに含まれる頂点同士の接続に関与しない見掛けの本数がe_2となります。また、純粋にv_in内の頂点同士の接続を行う辺の見掛け上の数がe_1になっています。
　図で内容を確認します。以下の図で青の頂点をひとつながりにする必要がなく、青マスを経由せず直接部屋内の頂点同士を手書きの辺で繋げてよいという状況を考えます。青の頂点を経由せず、分断した白マス同士に直接辺を引いてやれば外部有効辺は4本あれば足りるので e_1 - c_out = 4 となります(この図の場合はc_out = 0)。このとき、実際の盤面で青の頂点の接続に使っている、部屋内頂点の接続から見て不要な数が e_2 = 3 (= v_out) となります。

上記ではv_in = 5となる（へや内の分離した白マス領域を数える）
頂点を数えるとv=e+1からこの状態では外部の有効辺e_1が4本あれば足りることもわかる

　このあたりまでの内容を理解できれば、ペナルティ計算を意識しなくても、「今の状態からどれだけ有効辺数の得をしたらひとつながりになるのか？」という考え方だけでペナルティへやわけは解けるので、基本的には各種式や細かいペナルティの分類等の諸々を覚える必要すらなくなります。
　本記事でこれ以降①~⑧式あたりに何度も言及するのでスクロールしないで済むようにウィンドウを複製するかメモ帳に式だけを張り付けるかしてウィンドウを並べておくことをお勧めします。

ここまでのまとめ

　注目していない領域には頂点がなく辺の役割だけ果たすとして盤面を見た時に、辺の数と注目している領域の非連結成分数で辺と頂点とループの関係式を書いたものが⑥です。注目してない領域にも頂点があるとみなした場合の式が⑤となります。また、v_in (= v_in_def + p_diff)は
v_in = 3N + v_b - e_b - 2X - Y + c_in
を使って各部屋について基準状態を使わず直接計算することができます。
また、より簡便に
3N + v_b - e_b = v_in_def + 2X_def + 2Y_def - c_in_def （⑨式）
を使えば適当に盤面に黒マスを埋めるだけで簡単にv_inがわかります。

ペナルティへやわけの雑な解き方について

　筆者はペナルティへやわけをだいたい⑤～⑧式あたりで解いています(有効辺数があといくつ必要としか考えていないのでどれとは意識していないが)。繰り返しになりますが、これを使うメリットはv_in_defは盤面をとりあえずでいいので埋めれば非連結な白マスの組を数えるだけで簡単に得られるため(大抵は数個程度)、サイズのある盤面でも初期盤面でへやの辺と頂点の数を計算する必要がないことです。結局⑦式の右辺の形で記されるように、ペナルティ発生がどれだけ許容されるか、あるいは外部に追加辺を確保するかがペナルティへやわけの趣旨になるので蛇足の面倒な計算はしたくない。
大体以下のようにいつも解いています。
1.とりあえず盤面の数字通りかつペナルティが最小化(+外部辺の数が最大化)されるように黒マスを埋める
→簡単に最適化が分からなければとりあえず適当に埋めてよい。部屋内部で完全に分断される白マスがあってもよい。（黒マス隣接だけは禁止）
ここで有効辺数最大化を考えた仮埋めが一意であれば唯一解性まで確認できるので部屋の外の残りの盤面まで埋めて解答終了
仮埋めが仮埋めで終わって解がわからない場合、引き続き以下の手順
2.埋めた結果の白マス領域分割数を数える
→ここで後どれだけペナルティを減らす必要があるか、あるいは有効辺を外部に確保する必要があるかがわかる。
3.仮埋めの過程でペナルティが発生しそうな場所がほぼわかるので理屈を確認しながら最低限発生するペナルティを数える
＋
外部に確保できる辺の位置と数(最大充填数)を確認する
→大抵の場合はペナルティ最小化と辺の数の最大化はどこかで両立しないので有効辺確保の最大値をここで精査する。
5.盤面で確定しない部分までは全部消してから残りを埋めなおす。
→1.の手順でペナルティ最小化、辺の数最大化で一意に確定するところがあればそれはわかるようにしておくとよい(例えば確定黒マスに付随する白マスだけは埋めて置くなど)
これでほぼ引きみたいでも間違っていない楽な解き方ができます。文面だとわかりにくいと思うので最後に出す例題の解答手順を参考にしてください。

2.へやのグラフとしての考え方

　以下図のように盤面で長方形の盤面の全体に対して辺と頂点を数えるようなペナルティへやわけであれば辺と頂点の数は簡単に計算できます。

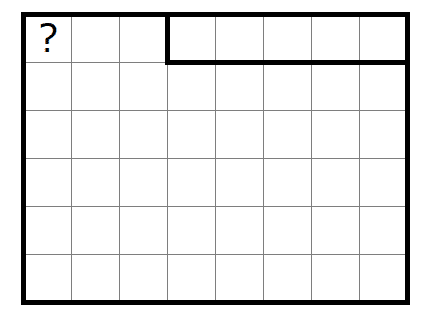
これが例えば以下のような盤面になると、盤面左上のへやに対してのみペナルティを考えたい場合には左上のへやとそれ以外のへやが白マスで接続している、白マスが接続しても一部に行き止まりがある、一部は右と下のへやがつながっている、など状況が複雑になるため簡単に辺の数が計算ができません。状況に応じて左上へやの辺をうまく数えてやる必要があります。

2.1.単純なへやの拡張

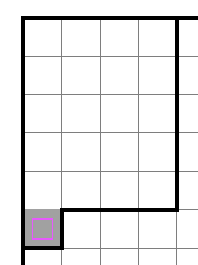
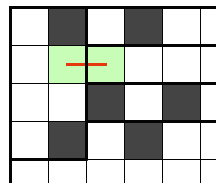
　以下のように単純にへやを拡張して一つのへやとして捉える方法があります。?のへやが1マス広いものと仮定し、代わりに広くした部分には?でカウントされる黒マスは置けない盤面として見てペナルティ計算を行います。
※画像で緑にした部分の外まで拡張しても結局はループの増加で相殺されて無意味なので、計算しにくくならないように必要最小限の1行1列拡張で止めておきます。

例題
　この例題で"雑な解き方"をする場合、部屋を拡張して考えてペナルティが最小化される置き方をします。とりあえず2*2が発生しないように置きつつ角辺に黒マスを充填します。2*2白マス回避と辺の黒マス最大充填が両立します。部屋の拡張をしたことで外部辺を考えなくてよいのがポイントで、⑥式の右辺が0になります。単に拡張した部屋内で全接続して頂点数1となればよいので、複雑な議論が不要になっています。有効辺数が最大化される置き方が一意になり、これ以上有効辺が少ないと分断することがわかるので他に解のパターンが存在しないことが確定します。つまり、作成した標準状態に対してそれと同等またはより効率的な黒マスの置き方：p_diff≦0 となる別の置き方は存在せず、効率が悪いp_diff>0となる置き方では分断が発生することから唯一解性まで確認できます。
　大体の問題はとりあえずこのパターンで部屋を一定の範囲拡張して考えれば解けます。一行一列全て拡張ではなく、数マス追加でくっつけるくらいの拡張も考えます。

2.2.盤面のつながり方を模式化したグラフとしての拡張

　これも使うことはありますが2.1.の拡張を部分的に行うのが基本的にはよいです。外部辺とペナルティのバランスを考えるのは面倒なので、言っていることが同じなのであれば見やすい部屋拡張の方が楽。2.1.の例題での10のへや左下のように拡張時に角扱いのマスが減るのもへや拡張で解くと楽なポイント。
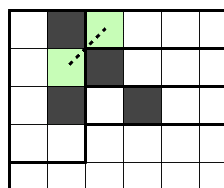
　以下の盤面で左上の部屋のペナルティを考える時、1のへやの黒マスがどこに入るのかがわからないため、2.1.の単純なへやの拡張では少し扱いにくくなりました。ここで図の右のような頂点と辺を仮想的に考えてみます。1のへや2つと外にあるへやもまとめて一つの頂点として扱っています。図で書いた緑の線がe_out、緑の円がv_outにあたります。1のへやの黒マスを左上へやと接するように置いた場合はe_outがその数だけ減ると考えます。

　注意点として、グレーアウトしていない一番右下のマス(？大部屋の右下角)は仮想頂点と2接続(マスの右辺と下辺が外部頂点に接続している)なのでこのループがどこかで切断段されないと有効辺のロス(ループペナルティ)が発生します。
　この考え方で問題を解く場合、①式の右辺を最大化することで左辺のNがより大きい値でも許容されることから右辺の各変数の兼ね合いを考えることになります。左辺は定数なので⑨式等を使うでもよいので計算します。

　以下は考え方の例として記載しますが、本来は図に書いていない角辺の黒マス充填数が何個になるかも考える必要があることに注意してください。
この例では辺の本数が絡む部分を抜粋しているだけです。

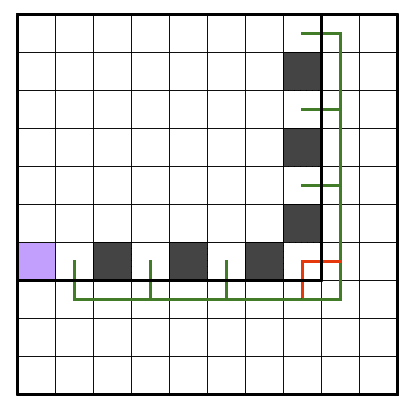
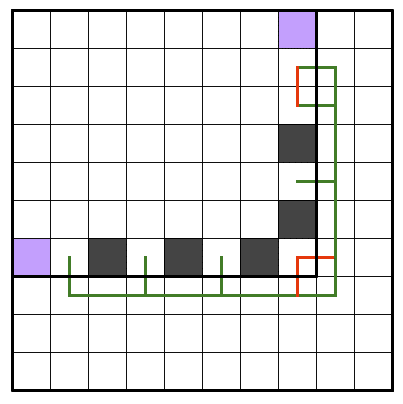
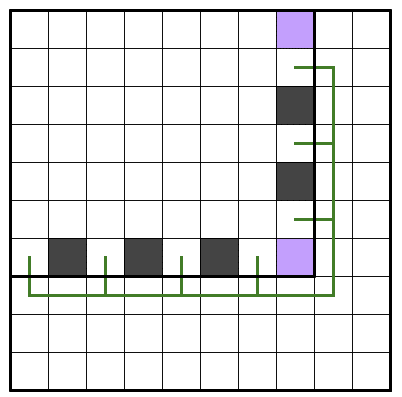
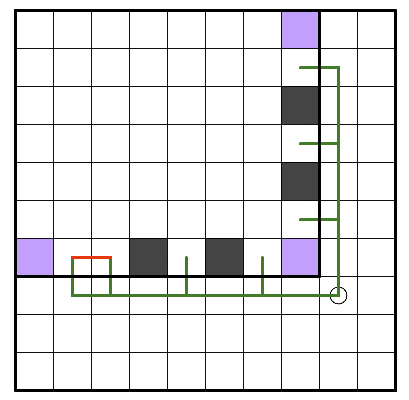
　上記4つの図を比べると、そのうち下二つのパターンが①式で右辺を最大化できることがわかります。最大化される場合だけ黒マスがもう一個入る、といった決まり方をします。
　実際の問題では例えば以下の図のような形で差別化されて片方に絞られることも多いです。

上記の例でわかるように、外部有効辺の数も絡む場合には部屋の角に黒マスを充填しなくても全体では損得が合計0になることがあります。部屋の辺の長さが偶数の時は特に注意しましょう。
　これについては特に例題は出しませんが、パズスクでcoggyさんがこの解き方で解ける日付ネタ問題を簡単なものも含めてたくさん出しているのでアゼンから選んで適当に解いてみてください。

3.川のグラフとしての考え方

　さて、やっと本題です。式を読み飛ばしてきた場合はここまでのまとめと雑な解き方だけでも読んでおいてください。
　ここでの話は⑤～⑧式のe_1、e_out、v_outがへやわけの川とどのような関係があって川がどのような特性を持つか、といった内容になります。

3.1. 川の白マスをグラフの辺/頂点に見立てて扱う際の白マス分類

　川に発生する白マスにはいくつかタイプがあるのでまずはその分類を行います。

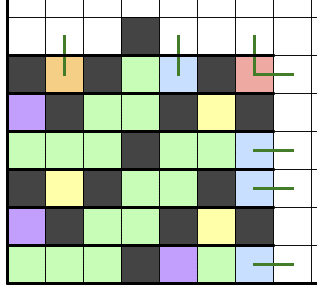
緑色：川のメインとなる白マス。青または紫で示した白マスとの間を繋ぐ辺の一部として扱う。白マスではあるが、後述青マスと緑マスのひとつながりの全体をまとめてグラフの辺扱いにするとわかりやすい。
紫色：川の緑マスがつながった先で盤面の壁(あるいは黒マス)に遮られてどこにもつながらない白マス。グラフの頂点として扱う。⑤式のv_outの一例。⑥式以降の形にして式の上では無視することになるが、後述の川の特性を考える上で数合わせとして川の末端にいることだけ意識しておく。
青色：川と外部領域の接合点。緑マスと同様にグラフ辺の一部として扱う。図のように青マスの末端部分は辺が飛び出していて川外部と接続するが、接続先未定の形で辺が存在して末端の頂点は存在しないイメージ。
黄色：川の途中にあるくぼみの白マス。グラフ連結には寄与しないので無視する。緑で色分けた白マスと辺でつながっているが、勝手にその辺を食いつぶしているため有効辺の観点で見る意味がない白マス。⑤式のv_outの代表例。見る意味がないので⑥式以降の形にして存在を完全に無視する。筆者はこの記事を書くまで存在を忘れていた。
橙色：川外部と直接つながっている頂点+辺扱いの白マス。頂点付きなので有効辺にはならない。有効辺0の役立たず白マスで、他の辺扱いとなる白マス(青マスなど)と接合しない限り単体での役割もないので黄色マスと同じく基本は存在を無視する。
赤色：文字通りコーナーケースの辺扱いマス。本来は上記の橙色マスと同じ立ち位置になるはずが、川の外部と2方向接続できるので辺扱い。

　川をグラフとして扱うとき、基本的に
・青マス→緑マス→青マスの形からなる辺（川外部の白マス同士をつなぐ辺)
・青マスから紫マスまでをつないだ辺と末端の紫マス頂点
（川外部の白マスから伸びる辺と頂点)
・赤マス単体の辺
これらの辺と頂点の集合として扱います。川と川の垂直接合等で川の成す辺が直接橙マスに刺さる場合は橙色の存在も意識します。黒マスはこれらの白マスの仕切りでしかないので、川のグラフとしての扱いに限って言えばあまり黒マスを意識する必要はありません。

3.2. 川の辺扱い白マスと川外部の接合点について

　以下の図では、川の出口の辺扱いマス(3.1.の青マス)が2マス使って外部に接続していますが、これは外部マスと合わせてループを形成しているため、川領域と外部の接合における有効辺の数は1となります。川の外側に黒マスがあればその場合もやはり有効辺数は1となります。よって、いずれの状況であれ川の白マスと川外部の白マスは有効辺数1で接続されます。(要するに川の出口の太さをグラフ辺としての扱いの考慮に入れなくてよいということです。)

川出口で白マス2つが川外部と接合している状況ではループが発生し、
2領域間を接続する有効辺数は1

3.3. 辺/角の川における白マスの再帰的発生とグラフ形式の対応

　川の特徴の一つとして、川の途中で脱出しようとすると白マスが脱出した反対側から再度川に発生するというものがありました。以下は3本川で盤面外周に接しているパターンです。

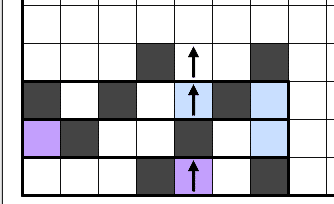
　3n本川をグラフとして見た際の有効辺の数を考えます。川の黒マス白マスが3マス先にコピーされる手筋があるので3n本の代表として3本川を例に取り上げて考えます。
上の図では辺の数e = 2、行き止まり(頂点) v = 2なので有効辺数は e - v = 0、下の図ではe - v = 1 - 1 =0です。
　盤面の辺に川がある場合、左の紫マスが青マスになると見てやればわかりますが、紫の頂点扱い白マスがいずれの場合も1つなくなるので有効辺数は上図で 2 - 1=1、下図で1 - 0 =1となります。
　盤面外周以外に川がある場合については後で扱うのでここでは割愛しますが、このように再帰的白マスが外周から発生したとしても3n本の川であれば頂点と辺が同時発生するので盤面全体から見て有効辺の数は変わらないことになります。辺の3n本川であれば有効辺の数はn+赤マス数になります。角の川であれば赤マス数が有効辺の数。

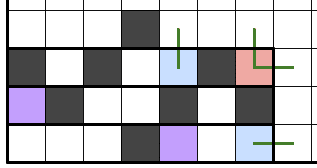
　以下の図のように川の白マスの出口に角の赤マスが一致する場合もやはりn+赤マス数となる。

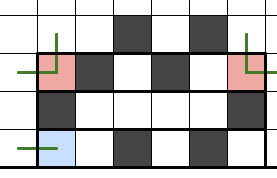
　また、川底の黒マスから両隣で再帰構造を作ることができますが、この場合も結局紫マスと青マスが対応していることは同じなので有効辺数はn＋赤マス数です。通常と本数は変わりません。

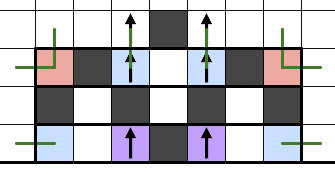
　3n + 1本、3n + 2本川だと再帰発生を起こした場合の有効辺カウントは複雑になります。再帰が出るパターンを辺に使った問題を作ったことがないのであまり検討していません。
・3n + 1本川の場合

一マス上流側で先に再帰発生が起こって下流側で脱出が起こるパターン
再帰発生した箇所の下流に川が続いていれば必ず脱出が起こる
有効辺数は辺の川であればnが基本で
上記の再帰が発生しないパターンを川の残り領域に組み合わせることで有効辺数が増えていく

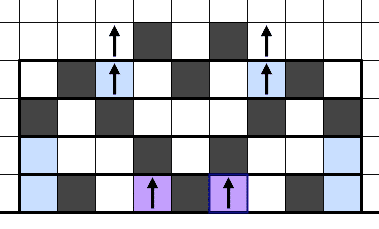
3n+1本川では川底黒マスから両側に再帰発生すると有効辺数はnが基本で、
上記の再帰が発生しないパターンを川の残り領域に組み合わせることで有効辺数が増えていく

・3n + 2本川の場合

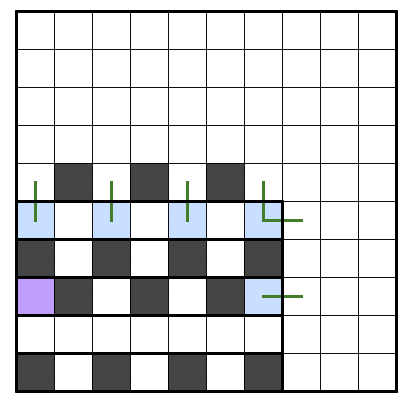
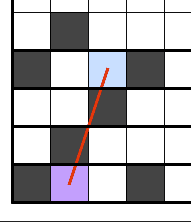
一マス上流側で先に脱出が起こって下流側で再帰発生が起こるパターン
脱出が起こったマスの横に黒マスがあれば、その黒マスの川底方向で脱出が起こっている
有効辺数は辺の川であればn+1が基本で
上記の再帰が発生しないパターンを川の残り領域に組み合わせることで有効辺数が増えていく

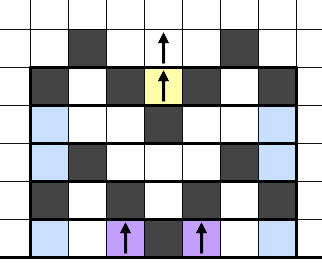
3n+2本川でも川底黒マスから両側に再帰発生すると有効辺数は基本数がnで、
上記の再帰が発生しないパターンを川の残り領域に組み合わせることで有効辺数が増えていく

　いずれの川の本数でも、川の脱出と再帰発生がリンクしないパターンで川全体が埋められると再帰発生を起こす場合より有効辺の数が多くなるので大抵こちらのパターンで埋めることになります。図を見てわかる通り川の長さや川の出口が角に来るかなど状況次第で有効辺の発生本数が変わるので実際の問題の状況に合わせて考えます。また、川が角ではなく辺にある場合、紫マスが青マスになることで有効辺の数が増えることも意識します。
　3n±1本川で再帰発生構造が絡むと辺の数が複雑になるので具体的にどのような埋め方があるか見てやって、この場合だから○本みたいな短絡はしない方が良さそうです。
※へやのグラフとしての考え方2.2.冒頭で書いた通り、グラフとしての模式化をするより単純なへやの拡張に落とし込んだ方が楽です。ということで、辺や角の3n±1本川を実際の問題に適用する場合には川の表面を川外部にあるへやの一部として拡張して解きます。大抵の場合は川表面と部屋の接面をほぼ全部白マスにしてへや側の有効辺を稼ぐことになるのでその方が簡単です。

3.3. 中空の川の辺充填

　3.2.では辺と角の川を見てきたので中空の川について考えます。3.2.で触れたように再帰構造を中途半端に絡めると複雑なので以下の例のような単純な場合だけここでは考えます。必要になったとしたら状況次第で以下2つの例の形を組み合わせること、川の構造単位毎に川を区切って考ればよいはず。

3.3.1　ジグザグ黒マス配置の中空川
　3n本川（図の緑）、3n+1本川（図の青）、3n+2本川（図の赤）と川の本数を増やしていった際の辺の増え方を図示します。川の上流下流を結ぶn本の辺を基本に、角マスなどで辺を獲得します。川が流れの方向に長い程に川の表面と底面に垂直な辺を追加で獲得します。

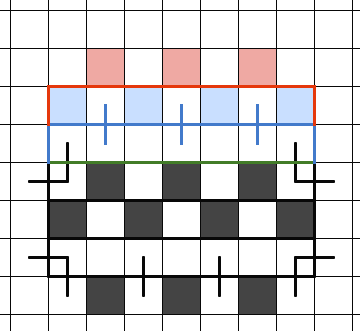
3.3.2　斜め一方向つながりの黒マスで埋められた中空川
　同じく3n本川（緑）、3n+1本川（青）、3n+2本川（赤）と川の本数を増やしていった際の辺を図示します。この構造の場合、川が流れの方向に長い程再帰構造の発生回数が増えて辺が増えます。3.3.1の構造の方がトータルの辺数は増えますが、辺によってつながる領域の位置関係が違うので状況次第でこちらを使います。たとえば川表面に接しているへやで有効辺が余っていれば3.3.1の構造を使ってもへやのループが増えるだけで辺の無駄遣いになります。その場合はこちらを使用することになります。

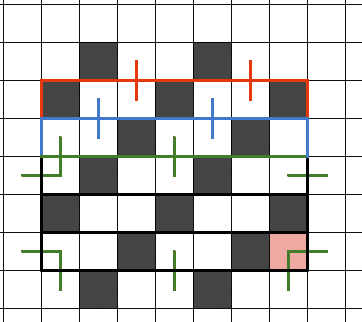
4.ここまでの考え方を使った例題解説

　以前パズスクに投稿したこちらの問題を解説します。例題と言えるか怪しい難易度ですが、考え方を網羅的に使ってかつ盤面がそれなりに見やすい例題としてこれ以上は用意できる気がしないです。

4.1.解答方針の把握

　まずは適当に大部屋に黒マスを指定された数だけ埋めて、有効辺が各部屋でどれくらい足りないか見てみます。盤面の川領域は本数を数えてやって、外周の4本川と5本川は最初からへや拡張に使うことにします。拡張部分に川の黒マスが入ると分断が発生してペナルティ発生です。あまり使いませんが意識の片隅にしまっておいてください。中央14のへや右辺と下辺で拡張した部分は白マス記入してあります。

　また、へやの内部で川と接しているところでは黒マスと白マスが交互にならないように配置しておきます。川をグラフ辺の集合としてみる、という考え方を使っていくわけですが、後の図のように川で用意した辺をへや側から塞いでしまうと盤面全体で有効辺のロスになるからです。この部分についても上記盤面でわかりやすいように白マス記入してあります。

　黒マスを埋めた結果を見ると、中央14のへやは単体では辺が全然足りていないことが分かります。へや拡張してもまだまだ分断が残っています。それに対して他の部屋は適当に置いた状態でひとつながりにできるのでペナルティ的には中央14より余裕がありそうです。この問題は中央14のへやをどのようにして盤面全体を使ってひとつながりにするかという解答方針で解くのが良さそうとわかります。

4.2.盤面全体の辺と頂点の数の概算把握

　現状での各へやのグラフ頂点数と川が成す辺を数えます。青で示した辺3本という数字について、川の流れ方向に2本のグラフ辺があり、更にそのうち川表面の1本が中央14へやの拡張部分とつながると見れば合計3本です。
盤面上辺の川で角白マスを使った辺が形成されればデフォルトの2本よりその数だけ辺が増える可能性があります。？の部分は後で見ていくのでここでは置いておきます。現時点では辺の数に余裕がありそうなのでどこかでロスが発生すると思われます。具体的に見ていきましょう。

基準状態での辺と頂点の数概算
赤が頂点数(v_in暫定値)、青が辺の数(e_1暫定値)
まだ概算なので不正確

4.3.へやのペナルティ最小化と外部辺(川)の両立可否

4.2.の概算だけで見ると辺の数に余裕がありそうだったので有効辺のロスが発生しないかを見ていきます。
　まず一つ目、4本川と5本川の平行な2辺についてのロスを確認します。以下の図のように、平行に走っている辺が同じ頂点同士をつないでいるので、へや間でループが形成されるか、辺が実際の盤面では何かしらの黒マスによって遮られているか、へやのペナルティで分断した領域を繋いでいるか、どの場合であっても4.2.で見た基準状態と比較して最低1ロスは発生します。

　続いて、4本川に実際に黒マスを埋めてみます。そうするとループによるロスどころか角の黒マスによって2本の辺が両方とも切断されて7と8のへやをつなげないことが分かります。川に接した角4つ全てに充填しないとして、7のへやの左辺に3つ黒マスを充填すれば下の川で破綻し、8のへやの左辺に3つ充填すると黒マスを詰めることで川の成す辺との切断で1ロスです。1つだけ黒マスを角ではなく部屋内部におくとすれば、へやの有効辺数に余裕がない（ループが残っていない、へやが既に木構造のグラフとなっている）これらの部屋ではどちらで角ペナルティが発生しても分断が発生します。よって、いずれの場合にせよへやのペナルティまたは川の辺の切断で1ロスが発生します。

14のへやを盤面拡張し、8と7のへやの角を全て充填した状態
ジグザグの向きが逆でも同様

4.4.中央14のへやの充填パターン比較

　中央14のへやの充填パターンはA面B面どちらに充填するかで大まかに2パターンあるのでこれを比較します。解説を称しておきながら申し訳ないですがここの14の部屋の決まり方をきれいに見通せるやり方はわかっていないです。右下の角を白マスにするパターンが7と8のへやの合わせ技で破綻するので、その過程をなるべく理詰めっぽく追っているだけになってしまいます。速い理詰めを思いついた方は教えてください。全体盤面の左半分にある11と14のへやはペナルティ負担押し付け放題のおまけ領域で制約は大したことないので右半分でどう決まるかを考える必要あり。

　右下角が白マスとなるパターンについて、以下の禁止系に気を付けて中央14のへやを分割充填すると上半分と下半分で7個ずつ入るとわかります。

　引き続き禁止系に気を付けながら更に細かく分割充填を行うと14のへやで以下の黒マスは確定することが分かります。すると7のへやの左に黒マスが最低二つ入ることになり、川による禁止系に気を付けながら黒マスを充填すると7の部屋が決まります。

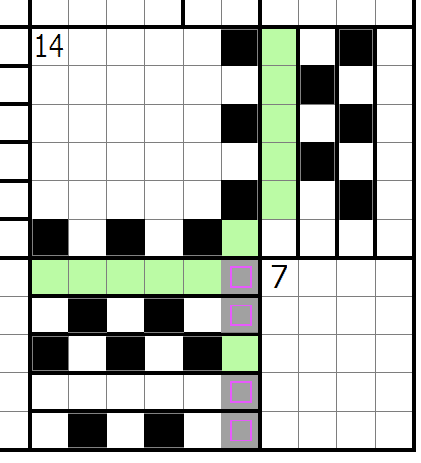
　7の部屋を埋めると8のへやの右下が白マスで確定します。ここから8のへやの充填パターンを試すと川の3連禁制約が絡んで全て破綻します。川に縦線が入ってるところの右側で黒マス合計12個入ることを使ってペナルティで行けたりしないかなとか、いくつか思うところはありますがわかりません。

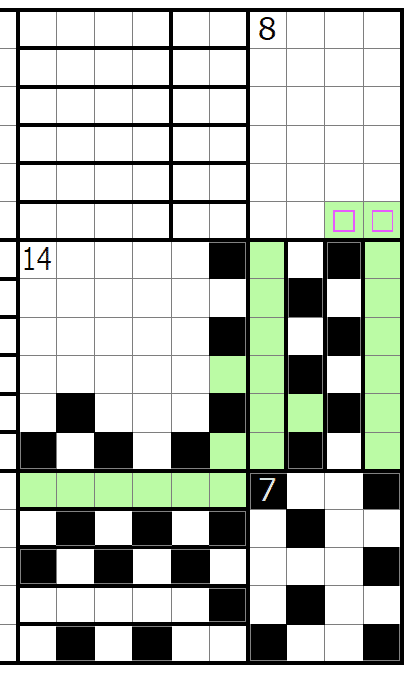
　14のへや右下白マスのパターンは破綻するので右下マスが黒になるパターンで解き進めます。
　逆面の充填パターンの左辺について、以下の充填が破綻することから14のへや左辺で最低1ペナが確定。

上辺の充填では以下の形の破綻系が上辺のどちらかに必ず発生してしまうので上辺についても1ペナ確定。（当然これら二つのペナルティは角に置けないという形でまとめて2ペナの可能性もあります）

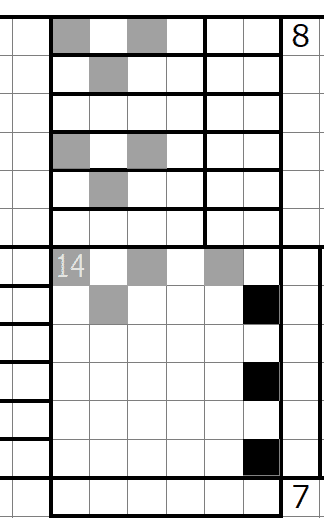
　中央14のへやは以下まで確定し、v_in = 4も確定します。左上領域で2つ、拡張領域同士はまだつながっていないのでそれぞれ1つで合計4つです。

4.5.上部川の角を辺として利用できるか

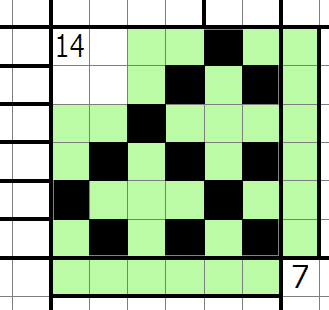
　~~上記で中央14のへやの充填パターンが確定したことで上部川の左側で辺の数を最大化しようとすると図の通り破綻することが分かります。~~
→すみません、ここの決まり方違いました。
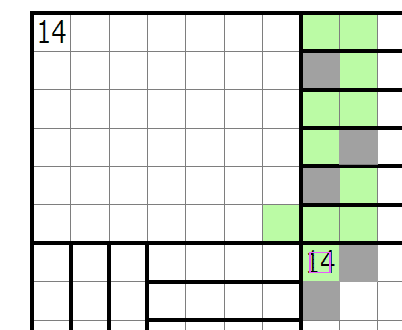
　左上14の部屋で右下の角に置けなくなるとペナルティで14のへやの頂点数が増えるので盤面全体でロスになります。仮埋めの盤面で下辺にこれ以上黒マスを詰め込むと左辺川との接続が途切れて1ペナルティ、右下角に置けず右辺に1個置くようにしても1ペナルティ、いずれにせよ仮埋めの状態と比較して1頂点増加します。

　上部川の右下を白マスにして右上8の部屋と接続したとしてもループが形成されるので無効辺になります。よって右下角も有効辺としての利用はできません。

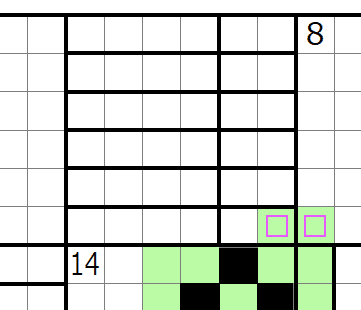
4.6.川の交差部分に発生するペナルティ

　続いて最初に概算の図で辺数を「？」とした川が交差している部分について、交差のせいでわかりにくいのでもう少し具体的に見てみます。盤面左側14と11のへやはペナルティに余裕があります。中空川をジグザグ黒マスで埋める方法で辺を稼ぐのは、これらのへやでは外部辺がなくとも頂点数1(ひとつながり)という仮定の下ではループが発生するだけで意味がないです。川を斜め黒マスで埋めて別のへや同士をつないで辺の数を稼ぐ配置を考えます。
　以下の図のよう垂直な川の接合を考えると、辺の役割を持つとした川の領域同士をつないでいることになるので、その接点には仮想的な頂点を考えてやる必要があります。よって、頂点の発生によって川同士で辺が接続した数だけペナルティが発生します。（今回は例を挙げませんが川の接続が垂直ではなく、同じ方向の川を途中で分割して考えた場合でも同様に間の仮想頂点が発生します）
　以下のように横向き川の角全てを白マスにしたとしても、川同士の接合は頂点発生によるペナルティが発生し、川の右上マスは14のへやの黒マス2パターンが1つに確定して切断されることからこの横向き川で角を白マスにすることによる有効辺の得はありません。よって、垂直に交わる横向き川では全ての角を白マスにして充填パターンとそれ以外のパターンで有効辺数は変わりません。角全てを白マスにしないパターンで考えれば頂点発生2、辺の数は3になります。

角を白マスにして辺を稼ぐ配置
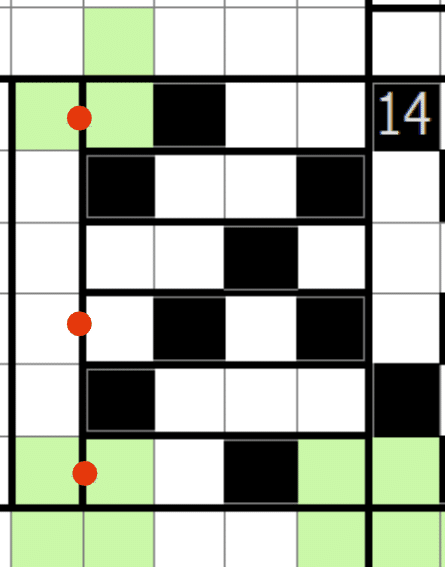
川と川の接合部（辺と辺の接合部）は頂点が発生する扱い

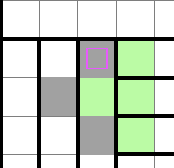
　補足ですが、以下の形が禁止系になるので、川の白マス分類色分けで示した橙マスと横向き川は接続しません。

4.7.頂点と辺の数、ペナルティ発生状況まとめ

　ここまで見てきたペナルティなどの情報をまとめたものが以下となります。赤が頂点数、青が辺数、茶色がペナルティ数や追加発生する頂点の数です。これらの数字で辺と頂点の収支を比較します。⑦式の各値について、
Σv_in_def = 1 + 1 + 1+ 1+ 4 = 8
e_1 - c_out ≦ 2 + 1 + 3 + 3 + 3 = 12
Σp_diff ≧ 2 + 2 + 1 = 5
⑦式：Σv_in_def = e_1 - c_out - Σp_diff + 1 よりこれ以上のペナルティ発生は許容されないことがわかります。あとは盤面全体をペナルティが発生しないように埋めていきます。

　この問題では特に意識する必要はないですが、上記の途中経過から、直行している川と図で記入済みのマスと14・11のへやとでループが形成されるとペナルティになります。例えば14のへやは内部のみでひとつながりになる頂点数1の領域にあたるので以下のような川の埋め方はループペナルティが確定します。

　14・11のへやで横向き川表面に充填すると斜め黒マス配置が実現できず今回の問題ではペナルティになるので禁止形です。

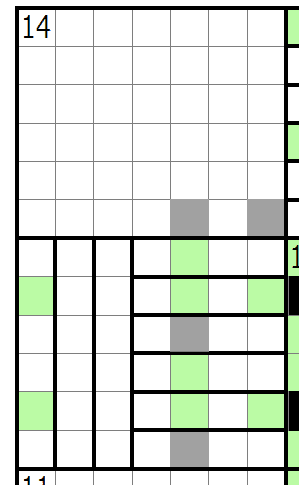
　ここから左上14のへやが決まります。外部辺による接続が0なので内部でペナルティや分断が発生しないように置いていくと一意に埋められることが分かります。

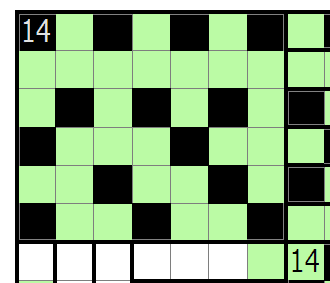
　左下11のへやでは左上角の黒マスを置くと破綻するのでここでペナルティが発生します。

　あとは11のへやが内部でひとつながりになること（つまり外部辺による接続が0であること）とペナルティに注意しながら埋めていけば一意に埋まります。これで完成です。

5.余談

　今回の記事では川を辺としてみなす、ということを行いましたが、別に川に限らずいくつかのへやをまとめて辺扱いしたあり頂点扱いしたりしても良いわけです。
　たとえば4 in 3*3のへやは折れ線型で2つのへやを繋ぐ、辺数1にあたるへやと捉えてもいいわけです。へやわけ盤面で部分毎にグラフとしての役割を設定してやることで見通しよく解ける問題もあるかもしれません。流石に川のように「この形ならこう」みたいな定型モノはもう出なさそうですが。

6.あとがき

　この記事を構想した元々の目的は最後の自作問題の解説でした。これだけの前提知識を用意しないと解説できないとは・・・適当にpzprRTで作ってこれ理詰めあるのかなってちょっと考えてみて、理詰め方針の概略だけ思いついた時はここまでとは想像もつかなかった。読み返し回数が少なくてミスの修正を全然やり切れてないのは気がかり。殆ど思い付きの文章で構成されてるようなレベル。
　読みにくい、わかりにくい、そもそも論理が誤っているところがあったら私のTwitterアカウント(@mukkitokonbu)にリプを飛ばしたりパズスクDiscordでmukki宛てにメンションするなりで伝えていただけると助かります。改善できるものは図を追加したり文面を変えたり対応したいと思います。