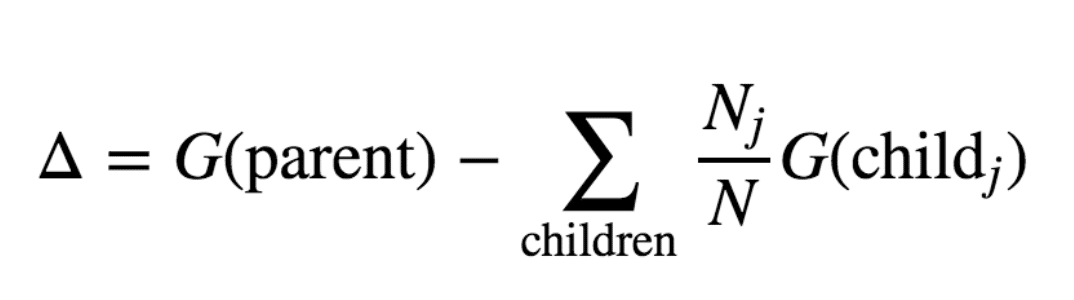決定木について
はじめに
みなさん、こんにちは。
今回は、機械学習のアルゴリズムの中でも、最も直感的で分かりやすい「決定木」について説明をさせていただきます。
機械学習とは
機械学習とは、ITによる新たな自動化を実現するための技術、或いは、学問です。
機械学習の説明については、以下記事に記載しておりますので、よければ参考にして下さい。
決定木とは
機械学習のアルゴリズムは多々ありますが、その中でも最も直感的で分かりやすいアルゴリズムが決定木かと思います。
或いは、最も基本的な機械学習のアルゴリズムとも言えるかもしれません。
決定木は、条件分岐によって、何かを識別するものです。
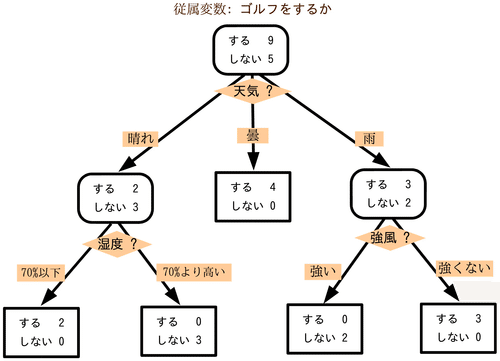
構造は以下のようになります。
(wikiに載っていた例)
例えば、とあるゴルフ場における、天気と来客状況の関係性について、決定木の学習アルゴリズムによって導出された決定木の構造が、上記図のような形になります。
これは、過去の状況と、それに紐づく結果が、上記図のようであったということです。
そして、その過去の傾向が、未来の傾向にも当てはまりそうであれば、過去の傾向から未来の予測をしてみようと、そういう運用を目指しているものになります。
もう少し具体的に説明をします。
例えば、とある期間14週の各週末について、とある調査対象のお得意会員様が、ゴルフ場に来場したかどうかを分析するとします。
それを先読みして、今後のゴルフ場運営における無駄を減らしたい、というモチベーションからです。
積み上げた経験則等から、どうも天候と関係がありそうな印象であったことから、特に、来場是否と天候との関係性を分析するにしました。
調査対象のお得意会員様が来場された日は、晴れていたか、曇っていたか、雨だったか。
湿度は高かったか、低かったか。
風は強かったか、弱かったか。
すると、傾向として、以下のことが分かりました。
曇りの週末は、必ず来場されていること。
晴れの日には、湿度が低ければ来場されていて、湿度が高ければ来場されいないこと。
雨の日には、風が強い場合には来場されておらず、風が強くない場合には来場されていること。
そして、これらの分析結果から条件分岐をまとめていくと、上記の決定木構造が導出されました。
もし、この決定木構造がロバスト(頑強・堅牢・強靭)に適用可能な法則性であったとしたら、この調査対象のお得意様については、来る週末の天気予報が出た時点で、来場予測が可能ということになります。
こんな形で導出された条件分岐による法則性が、決定木となります。
決定木の学習アルゴリズムについて
決定木という名称や表現方法でなくとも、決定木のような考え方を、人は普段から用いているかと思います。
そして、データを所望の形で分割できる条件を上手く見つけさえすれば、決定木構造は組むことができます。
つまり、手動でもその導出は可能であるということです。
しかし、データ数や、分岐条件対象のデータ項目などが増えてくると、その作業は困難となってくるかと思います。
それなりの時間は、一定必要となります。
或いは、分析方針や分析結果が、分析者の主観に寄ってしまうことなどもあろうかと思います。
そこで、決定木の学習アルゴリズムが有用です。
決定木の学習アルゴリズムは、多々ある機械学習のアルゴリズムの一種となります。
決定木の学習アルゴリズムは、コンピューターの計算速度を活かして、高速に決定木構造を導出してくれます。
計算速度が人に比べて圧倒的に速い為、分析時間も圧倒的に短縮されます。
また、基本的には極めて客観的に分析してくれます。
前提知識や思い入れなどが、コンピューター、或いは、決定木の学習アルゴリズム上には無い為です。
その為、人間の主観の外側にあるインサイト発掘にも、幾分かの期待が持てます。
或いは、アルゴリズムを調整して、ある程度の主観を持たせることも可能です。
実際に、決定木の学習アルゴリズムが、どのような計算手順によって、決定木を生成しているか、その手順を説明します。
学習アルゴリズムというと、高尚な印象を受けるかもしれませんが、実際に行っている計算は、意外と単純なものになります。
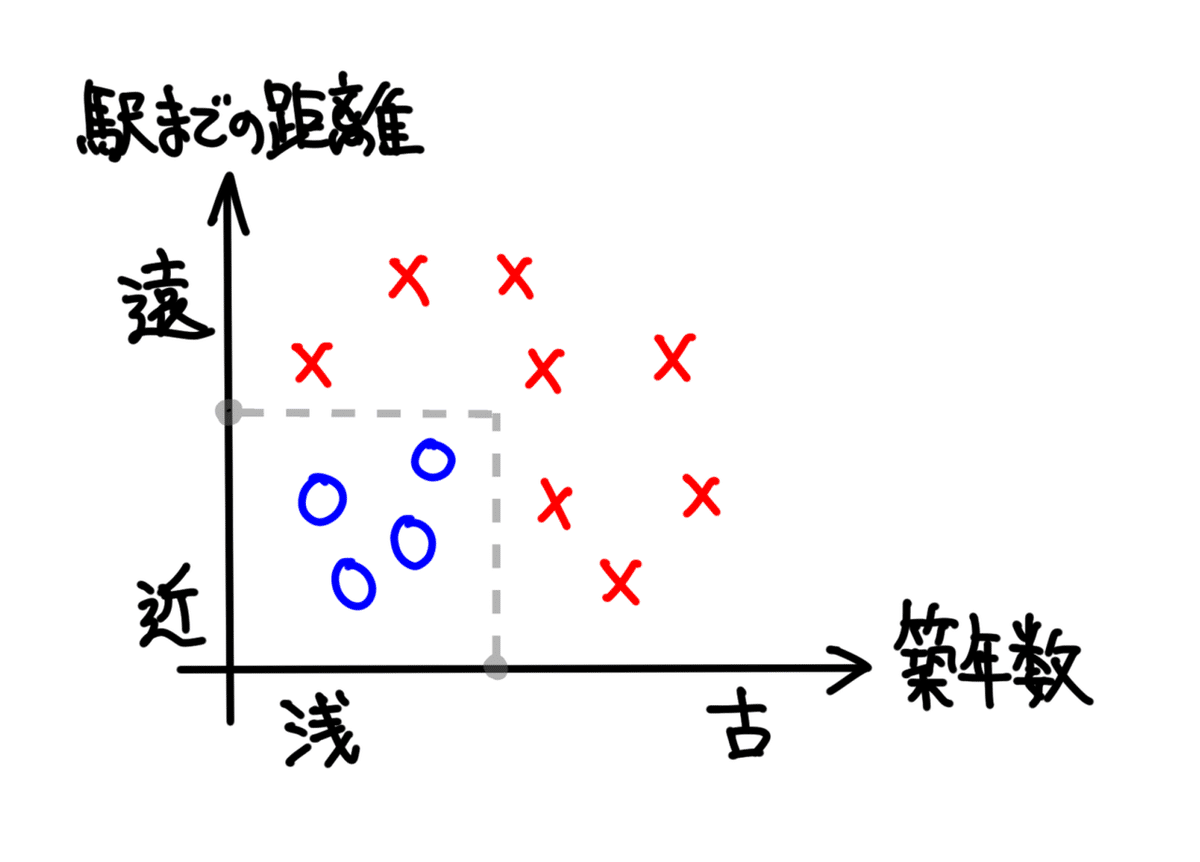
例えば、以下のようなデータがあったとします。

これは、すごくラフに設計した、不動産購入に関するデータです。
購入後に、賃貸運用や売却がしやすい物件を、青い◯で表しています。
逆に、賃貸運用や売却がしづらい物件を、赤い✕で表しています。
このデータを用いて、決定木の学習アルゴリズムを説明していきます。
◯となる条件は、「築年数」が浅いこと(いわゆる「築浅」)と、「駅までの距離」が近いこと(いわゆる「駅近」)とです。
その両方を満たした物件を、好条件の物件としています。
一方、✕となる条件は、「築年数」が古いこと(「築古」というそう)か、「駅までの距離」が遠いこと(「駅遠」というそう)かです。
この何れかを満たした物件を、好条件でない物件としています。
実際には、もう少し複雑な要素が絡み合うものだと思いますが、そんな感じに設定をしています。
或いは、集めたデータに関しては、そうであったという設定です。
人が、上記図のようなデータの分布を見た場合、好条件と判断される「築年数」と「駅までの距離」との線引はパッとできるかと思います。
例えば、以下のような形です。
一方、コンピューターは、人間のように図示化して客観的に眺めることなどはできません。
その為、ワビサビの効いた良い感じの境界線を直感的にパッと引く、ということはできません。
しかしながら、そこを上手いことやってのけるのが機械学習全般の考え方であり、決定木の学習アルゴリズムとなります。
あたかも人間がワビサビ効かせて引いたような境界線を、人間の指示通りにしか動作しないコンピューターでも引けるように、上手いこと計算指示を行う形でもってです。
具体的に、どうやってコンピューターが境界線を探索するかというと、仮説的に幾つかの境界線を適当(ランダム)に試し打ちしてみて、その中から最も良い感じにデータを分割できた境界線を採用するという方法で探索します。
つまり、「下手な鉄砲、数撃ちゃ当たる」という具合の力技です。
モンテカルロ法と言えば、ピンとくる方がいるかもしれません。
何度もランダムに、シミュレーションを繰り返して、得られた多数の結果から、最も良い結果を選別する形です。
ちなみに、モンテカルロ法については、別途以下の記事を記載していますので、よければ参照下さい。
ここで、決定木の学習アルゴリズムを、追いかけてみたいと思います。
先程の不動産データに対して、例えば、以下のようにランダムに条件を刻みます。

境界線は、◯と✕を上手く分断できるもの、或いは、比較的分断できているものが、良い境界線と言えます。
上の4つの境界線で言えば、左から2番目の境界線が、一番筋が良さそうです。
一番左の境界線は、「(左)◯:2、✕:1」と「(右)◯:2、✕:7」に分けられています。
左から2番目の境界線は、「(左)◯:4、✕:2」と「(右)◯:0、✕:6」に分けられています。
左から3番目の境界線は、「(左)◯:4、✕:5」と「(右)◯:0、✕:3」に分けられています。
一番右の境界線は、「(左)◯:4、✕:6」と「(右)◯:0、✕:2」に分けられています。
やはり、左から2番目が一番筋が良さそうです。
尚、この境界線の探索は、任意で別の軸でも行います。
境界線の試しもランダムならば、軸の試しもランダムという訳です。
別の軸というと、この図の場合には、「駅までの距離」になります。
例えば、以下のような形です。

一番上の境界線は、「(上)◯:0、✕:2」と「(下)◯:4、✕:6」に分けられています。
上から2番目の境界線は、「(上)◯:0、✕:5」と「(下)◯:4、✕:3」に分けられています。
上から3番目の境界線は、「(上)◯:2、✕:7」と「(下)◯:2、✕:1」に分けられています。
一番下の境界線は、「◯:3、✕:7」と「◯:1、✕:1」に分けられています。
中では、上から2番目の境界線が、最も良い境界線となりました。
しかし、その良さも、「築年数」の軸で探索した際の、左から2番目の境界線には負けました。
つまり、全ての探索の中で最も良かった境界線は、「築年数」の軸で探索した際の、左から2番目の境界線ということになります。
そうしましたら、それを決定木の最初の条件として採用します。

境界線が、晴れて1つ決定されました。
例えば、この条件の境界値を5年だとすると、グラフは以下のようになります。

この結果、決定木の条件分岐としては、以下の形となります。

こうして見ると、上手く条件分岐できていることが、改めて確認できます。
そして、ここから更に条件を切っていきます。
多段に条件を重ねる形です。
但し、築年数5年超の場合は、もう✕しか存在しないため、これ以上条件を分岐させる必要がありません。
ですので、条件分岐によって得られた右側の分岐先は、ここで打ち止めです。
分岐が更に続くのは、左側だけになります。

残る探索対象に対しても行うことは同じく、任意の軸について、ランダムに条件を試してみて、最も良い境界を採用します。

そして、以下の境界を採用します。

これによって、全ての◯✕が、境界によって分断された為、学習アルゴリズムの実施が完了となります。
尚、採用された「駅までの距離」の値を、「徒歩5分」だとすると、グラフと条件分岐図は以下のようになります。


決定木の学習アルゴリズムは、こんな形で実践されていきます。
尚、学習アルゴリズムの実践、及び、条件探索の完了は、全てのデータを分け切るまでか、条件の深さや数に対して設定をしておいた上限に達するまでか、という制御が一般的です。
境界条件の良し悪しを判定するための不純度について
先程の説明までで、決定木の学習アルゴリズムの大枠は、理解頂けたかと思います。
ただ、境界の良し悪しをどう判定するかについては、説明が曖昧だった、或いは、不十分だったかと思います。
これから、そこに対して具体的に説明をしていきます。
ちなみに、人間であれば、◯と✕の数を見れば、直感的にバランスを推し量ることが可能かと思います。
一方の割合が多く、かつ、一方の割合が少ない、という具合の判定がパッと行えるかと思います。
学習アルゴリズムにおいては、その実践を計算指示によって、実現をする必要があります。
或いは、上手く計算指示を行うことによって、コンピューターにその人間的な判定を行ってもらう必要があります。
どういった計算指示で、それを実現させると良いでしょうか?
その判定をさせる為には、厳密な評価指標を設けることが一般的です。
決定木の学習アルゴリズムにおいては、「不純度」と呼ばれる評価指標を用いることが一般的です。
尚、必ずしも不純度という指標を使わなければ、決定木の学習アルゴリズムが成り立たない訳ではありません。
学習目標と整合していれさえすれば、評価指標は何でも大丈夫です。
しかし、考え方がシンプル、かつ、効能が高いのが、不純度という指標であり、広く一般的に好まれているものかと思います。
或いは、古くからその方針で研究が進められている為に、それが踏襲されている形かと思います。
機械学習のライブラリとして有名なscikit-learnにおいても、不純度という指標が用いられています。
その不純度が、どんなものかというのを説明します。
不純度は、あるデータ集合における、特定の2つ以上のデータ属性について、その属性がデータ集合内でどのくらい混じり合っているかを示す指標となっています。
より混じり合っていなければ不純度が低くなり、より混じり合っていれば不純度が高くなるような指標となります。
具体的に、例を上げて説明したいと思います。
例えば、皆さんは「白」「黒」「灰色」という色を御存知かと思います。
(リンクのサイトより、グラデーション図を拝借)
これらの色の混じり合いで言えば、純粋な「白」と「黒」という色味が、最も不純度が低い状態となります。
それらは、「白:黒」という形で色味を割合表記した時に、「白10:黒0」や「白0:黒10」などと表現される状態です。
つまり、一方の属性のみで構成される、混じり合っていない状態です。
これが、不純度が最も低い状態、或いは、最も純粋な状態で、この時に不純度はゼロとなります。
対して、「灰色」という色味は、不純度が高い状態となります。
特に、「白」と「黒」が同配分だけ混じり合っている「白5:黒5」の状態、即ち、中間的な「灰色」という色味が、最も不純度が高いものとなります。
「白5:黒5」の中間的な色に比べると、「白3:黒7」や「白7:黒3」といった、どちらかに寄った色の方が、不純度は低くなります。
つまり、いわゆる半々の時が最も不純度が高く、一方の属性の割合が増えていくに従って、或いは、減っていくに従って、不純度は段々低くなっていく形です。
そして、最終的に、一方の属性のみで構成されるに至れば、不純度は0になります。
不純度は、そういった指標となります。
如何に混じり合っているかどうかを計測する指標という訳です。
もう少し、具体例を上げてみましょう。
例えば、純粋な「豚骨スープ」や「魚介スープ」は、不純度が低い状態になり、それらを混ぜ合わせて作られる「Wスープ」は、不純度が高い状態になります。
或いは、遠心分離機にかける前の「牛乳」を、不純度が高い状態とするならば、遠心分離によって分かれた後の「水分」や「生クリーム」は、不純度が低い状態となります。
或いは、「牧場」や「リス園」は、不純度が低い状態になりますが、「動物園」は、不純度が高い状態になります。
実用上、属性は2つであるケースが多いかと思いますが、3つ以上あっても不純度は適用可能となります。
不純度の種類
不純度の種類は幾つかあります。
例えば、機械学習のライブラリとして著名なscikit-learnというライブラリにおいては、以下の2つの不純度が用意されています。
(1)ジニ係数
(2)エントロピー
この2つが、決定木の学習に用いられる一般的な不純度かと思います。
これらについて、説明をさせていただこうと思います。
先ず、前者の(1)ジニ係数ですが、以下の式で表される指標となります。
(リンクのサイトから拝借)
シグマ記号は、総和を表す記号になります。
シグマの下に「i=1」と書かれ、上に「n」と書かれているのは、繰り返し行われる足し算の際に適用される添字を表しています。
シグマ記号の配下に、Ciと書かれていますが、総和の際にはこれが、C1、C2、C3、…、Cnという感じで繰り返されるという意味です。
また、Ciの説明は、式の下のコメントにてクラスだと書かれているので、先程の説明の例であれば、◯と✕の2種類になります。
つまり、nは2となります。
また、p(Ci)は、クラスの確率/割合と表現されています。
p²(Ci)とは、p(Ci)を2乗するという意味になります。
例えば、先程説明に用いた不動産データにおける条件分岐にて、各状態におおけるGini係数を計算すると、以下のようになります。

計算した結果を眺めると、◯と✕が混在している場合に、Gini係数の値が高く、混在していない場合に、Gini係数の値が低いことが伺えると思います。
また、完全に◯のみか、✕のみに分けきられた状態においては、Gini係数が0であることが確認できるかと思います。
これが、先程説明させて頂いた不純度の、具体例となります。
白黒のグラデーションでも、Gini係数を計算してみましょう。
仮に、白と黒の混ぜ具合は8段階とし、お互いの色味の強さの合計値は8となるように調整します。
つまり、割合として捉えるということです。

こんな形になります。
ちょうど半々の際に、Gini係数が1/2となっています。
2つの属性を持つデータで言えば、Gini係数は、値が一番高い時、即ち、属性が一番混在している時に、1/2という最大値を取る考え方になっています。
つまり、Gini係数が1/2であれば、2つの属性が半々に混在していると判断できます。
また、片側の属性のみで構成され、全く混在していない場合は、Gini係数が0となります。
つまり、2属性のデータでは、Gini係数は 0〜1/2 の値を取る考え方となっています。
この不純度という考え方が、決定木の学習アルゴリズムに導入されています。
適当に条件を沢山試していく中で、このGini係数を極力下げるような境界条件を探索するのです。
それによって、機械的な判定を、人間の直感に近い形にします。
次に、後者の(2)エントロピーの説明をします。
式は以下のようになります。
(リンクのサイトから拝借)
実は、エントロピーという指標は、Gini係数とすごく似た形になります。
横軸に片側属性の割合、縦軸に不純度を取ってグラフで比較してみると分かりやすいです。

どうでしょうか?
すごく形状が似ているかと思います。
尚、不純度は、適当に引いた複数の境界線について、それらの良し悪しを判定することを目的とした、相対的に行うものになりますので、絶対値の大きさにはあまり意味がありません。
また、2属性のデータに対して、エントロピーは、0〜1の値を取る形となっています。
Gini係数は、0〜1/2の値を取る形となっています。
仮に、値域を合わせる形で、Gini係数を2倍してみると、グラフは以下のようになります。

こうすると、概念が近いことが更に分かるかと思います。
情報利得について
不純度を理解して頂いたところで、次に、その使い方について、説明をします。
良い境界線を選ぶ際には、境界線による不純度の下がり具合を求める必要があります。
分割後の不純度を見るだけでは不十分です。
境界線で分割する前の状態における不純度と、境界線で分割した後の状態における不純度との差を評価する必要があります。
また、分割後の状態は、2つ以上に分割されている各状態について、不純度を求める必要があります。
また、不純度そのものはデータ数に依らない指標となりますが、境界線を選別する際には、データ数についても配慮をする必要があります。
例えば、以下の例を見て下さい。

この条件分岐については、どちらの方が有効と言えるでしょうか?
分割パターンAでしょうか?
分割パターンBでしょうか?
これは、一般的な決定木の学習アルゴリズムによれば、分割パターンAの方が良い条件と判断されます。
或いは、分割パターンBは分割する意義があるでしょうか?
これは、一般的な決定木の学習アルゴリズムによれば、分割する意義がかなり低いと判断されます。
この判断はどう行われるかというと、情報利得という指標を計算して、それによって行われます。
この指標は、不純度の値を用いて、データ数にも配慮をしながら、分割条件の良し悪しを判定するものとなります。
情報利得の計算式は、以下となります。
(リンクのサイトから拝借)
△が、情報利得を表しています。
Gは、不純度を表しています。
Gの中でも、G(parent)というのは、決定木の条件によって分割される前の不純度を表しています。
特に、式を拝借させて頂いたリンクでは、不純度をGini係数にて説明されているようですので、Gというアルファベットで表されています。
サイトによっては、不純度を表す英単語のImpurityの頭文字を取って、I(parent)と表現していることもあります。
G(Child j)というのは、分割された後の各分割先における不純度を表しています。
Nは分割前のデータ数を表していて、Njは各分割先におけるデータ数を表しています。
Njを全て足し合わせると、Nとなる形です。
Σ childrenについては、全ての分割先におけるものの総和という意味になります。
先程の分割パターンの例に当てはめると、情報利得は以下となります。
かなりゴチャゴチャとしていますが、これが集大成という感じです。

childrenは、childのleftと、childのrightという表現にしました。
そのように説明をしているサイトも多いです。
図の表記上も、child jを、child 1→left、child 2→rightとしています。
最終的に求められた情報利得(△)は、分割パターンAが 1/9、分割パターンBが 5/72 でした。
大小関係は、1/9 > 5/72です。
この際、決定木の学習アルゴリズムでは、情報利得の大きい分割パターンAが良い境界線として採用されます。
実際には、パターンC、パターンDと、もっと沢山の境界線も試し、最終的に最も高い情報利得が得られた分割パターンを、最も良い境界線として採用します。
尚、情報利得について補足をすると、例えば、◯と✕が完全に分割できた場合、分割後の不純度 G(child j) が全て0になりますので、分割前の不純度 G(parent)の値が、そのまま情報利得となります。
これは、分割前の不純度を全て解消することができた、という意味になります。
一方、例えば、以下のような場合は最悪ケースで、情報利得が無いことになります。

不純度が、分割前と分割後で変わっていないケースです。
こういったケースは、情報利得を計算してみると、0 になります。
ひょっとすると、この後段にてビシッと分割するための、アシスト的な分割である可能性もなくはないのですが、少なくとも上記の分割そのものは意味がないものと判断がされる計算仕様となっています。
その為、このような分割条件は、採用されることがありません。
また、情報利得はどうも、マイナスとはなり得ないようです。
私の手元でもシミュレーションをしてみましたが、それを肯定する結果が出ました。
以下、シミュレーションコードと出力結果です。
(※但し、浮動小数点誤差による、マイナス側のブレは起こり得るようでしたので、ロジックによっては包囲網を敷く必要があるかもしれません。)
# set param
num_simulation = 1000000
gain_info_stock = - np.ones([num_simulation])
N = 100
# loop of simulation
for i_sim in range(num_simulation):
# make parent data randomly
y = np.random.randint(0, 2, [N])
# set number of left/right data
N_left = np.random.randint(1, N)
N_right = N - N_left
# make index of left/right data randomly
idx_tmp = np.random.permutation(np.arange(N))
idx_left = idx_tmp[:N_left]
idx_right = idx_tmp[N_left:]
# split to left and right
y_left = y[idx_left]
y_right = y[idx_right]
# calculate G(parent) and G(left) and G(right)
gini_parent = (1 - (np.sum(y == 0) / N)**2
- (np.sum(y == 1) / N)**2)
gini_left = (1 - (np.sum(y_left == 0) / float(N_left))**2
- (np.sum(y_left == 1) / float(N_left))**2)
gini_right = (1 - (np.sum(y_right == 0) / float(N_right))**2
- (np.sum(y_right == 1) / float(N_right))**2)
# calculate infomation gain
gain_info = (gini_parent - (N_left / N * gini_left)
- (N_right / N * gini_right))
# stock infomation gain
gain_info_stock[i_sim] = gain_info
# show result
plt.figure(figsize=(10, 6), dpi=100)
plt.hist(gain_info_stock, bins=50)
plt.grid()
plt.title('np.min(gain_info_stock) = %.10f' % np.min(gain_info_stock))
plt.show()
print('np.min(gain_info_stock) =', np.min(gain_info_stock))
以下のstack overflowでも、情報利得がマイナスになり得ない旨を説明をしてくれていますので、興味がある方は参照下さい。
また、補足ですが、決定木の境界線による分断については、今回説明させて頂いたのは条件の度にデータを2分割するものでした。
特に、この分け方をする決定木は、2分木と呼ばれるものです。
決定木の学習アルゴリズムとしては、或いは、生成される決定木の構造としては、3分割以上の分割を行うものもあり、そのように促すことも可能です。
ただ、3分割以上の分割を行う決定木は、そのアルゴリズムの複雑さに対しては、精度貢献が低いようで、あまり一般的でないかと思います。
例えば、scikit-learnなどは、2分木の決定木アルゴリズムのみを実装されています。
今回の説明、及び、scikit-learnが採用している2分木の決定木構造、及び、その学習アルゴリズムは、CARTと呼ばれる種類となります。
他にも種類はありますので、興味の有る方は、是非掘り下げてみて下さい。
以下は、画像のリンク先に紹介されている、CART以外の決定木のアルゴリズムになります。
決定木の構造から求められる、特徴の重要度について(explainable AI)
出来上がった決定木の構造は、なぜその判断に至るのかという理由が、とても追いやすいものとなっています。
更に、その説明性の高い構造を活かして、特徴の重要度を計算する方法、或いは、そういった考え方が存在します。
これは、決定木が深く複雑に分岐した場合などに、ざっくりと貢献度の高い特徴が何かを判断するのに役立ちます。
尚、特徴とは、データの軸のことです。
冒頭に説明に使用した、不動産購入に関するデータで言えば、「築年数」と「駅までの距離」が特徴となります。
説明変数と言ったりします。
ちなみに、それに対して、◯や✕といった、過去の結果値、及び、未来において予測をしたい属性のことを、目的変数と言ったりします。
重要度は、過去の特徴と結果の関係性において、重要であった特徴と、その度合を示すものとなります。
その意味では、精度が高い決定木の重要度は、信頼性の高い重要度となり、精度の低い決定木の重要度は、信頼性の低い重要度となります。
万能ではありませんので、そこのところは慎重にお取り扱い下さい。
あくまで、作られた決定木の構造において、特に重要視している特徴とその度合を示す、決定木のお気持ちとなります。
尚、重要度の計算方法は幾つかありますが、情報利得の考え方を応用したものが、恐らく一般的かと思います。
scikit-learnでも、情報利得の考え方を応用した計算方法にて、重要度を計算しています。
scikit-learnが実施している計算方法については、以下の記事に詳細に記載されていますので、よければ参照下さい。
記事にも書いてありますが、重要度の計算方法は、抽象的にザックリ説明すると以下です。
(1)決定木構造における上部の条件に多用される特徴が、重要度が高い
(2)より情報利得の高い分割を実現している特徴が、重要度が高い
(3)より多くのデータを分割している特徴が、重要度が高い
これを眺めると、「なるほど」「まあ、そりゃ、そうだよな」という風に感じるかと思います。
或いは、そう思ってもらえたら、もう半分は重要度の概念を理解しているかと思います。
言ってしまえば、これ以上でもこれ以下でもありません。
もう少し具体的に、重要度を説明すると、以下となります。
(1)分割条件毎に計算される情報利得に、分割前のデータ数を掛けたものを、全てストックしておく
(2)分割条件に用いられている特徴毎に、(1)の合計を求める
(3)(2)の各値を、全特徴の(2)の値の合計で割る
つまり、より多くのデータに対して、情報利得が高くなるような分割条件を作ることができた特徴が、重要度が高くなります。
かつ、(2)の計算仕様から、幾つもの分岐条件に複数回が用いられる特徴が、重要度が高くなることも読み取れるかと思います。
(3)の計算については、全特徴の重要度の総和が1になるように、値を正規化しているに過ぎません。
重要度がスケールの整っていない絶対値であると、直感的に意味が捉えづらい為、重要割合100%を各特徴で分け合うようなスケーリングをすることで、より直感的に捉えやすくしている形です。
ここから先は
¥ 10,000
この記事が気に入ったらチップで応援してみませんか?