機械学習「基本のき」、回帰分析について(前編)
はじめに
皆さん、こんにちは。
今回は、機械学習の「基本のき」である、回帰分析について、書かせていただこうと思います。
機械学習とは!?
機械学習とは何か、という話については、以下に書かせてもらっておりますので、よければ参照下さい。
回帰分析とは!?
回帰分析とは、機械学習の基本的な手法、或いは、アルゴリズムです。
また、多くの機械学習アルゴリズムの源流の一つと言えます。
昨今、大変流行しているディープラーニングも、回帰分析を端に発するものです。
回帰分析が進化した末に、ディープラーニングが存在します。
そんな回帰分析ですが、その目的は、過去のデータから、現象の傾向を掴むことにあります。
そして、その傾向を、これから起こる未知の結果に対して、予測することに使用します。
例えば、不動産価格などで考えてみましょう。
東京近郊の分譲マンションの価格を調べてみたところ、以下のようなデータが存在しました。
(※少し加工しています…。)
家の広さ:x₁ = 36.50㎡ 不動産価格:t₁ = 1,900万円
家の広さ:x₂ = 45.70㎡ 不動産価格:t₂ = 1,700万円
家の広さ:x₃ = 62.50㎡ 不動産価格:t₃ = 2,900万円
家の広さ:x₄ = 66.30㎡ 不動産価格:t₄ = 3,800万円
家の広さ:x₅ = 72.10㎡ 不動産価格:t₅ = 3,400万円
家の広さ:x₆ = 74.50㎡ 不動産価格:t₆ = 3,900万円
家の広さ:x₇ = 76.90㎡ 不動産価格:t₇ = 4,500万円
家の広さ:x₈ = 80.10㎡ 不動産価格:t₈ = 3,700万円
これを、プログラミング言語の python によって、グラフに描画してみると、以下となります。
# import basic library
import numpy as np
import matplotlib.pyplot as plt
# set x value and y value
x = np.array([36.50, 45.70, 62.50, 66.30, 72.10, 74.50, 76.90, 80.10])
y = np.array([ 1900, 1700, 2900, 3800, 3400, 3900, 4500, 3700])
# plot x and y
plt.figure(figsize=(8,5),dpi=100)
plt.rcParams["font.size"] = 12
plt.scatter(x, y, s=100, alpha=0.5)
plt.xlim(-10, 110)
plt.ylim(-700, 5700)
plt.xlabel('家の広さ(㎡)')
plt.ylabel('不動産価格(万円)')
plt.grid()

グラフに表したとことで、家の広さに応じて、不動産価格が上昇している傾向が見られると思います。
家が広くなるほど、不動産価格も高くなる傾向です。
そして、回帰分析は、このようなデータが与えられた時に、以下のような直線を引いてくれます。

概ね、人間がパッと見で想像した傾向がなぞられるような形で、直線が引かれているのではないかと思います。
回帰分析のアルゴリズムを適用すると、このような形で、データから直線が導出されます。
尚、直線の導出とは、y = ax + b という直線を表す式を導出することになります。
更に、具体的には、係数 a と b を導出することとなります。
ここで、x は、家の広さを表します。
y は、不動産価格を表します。
a は、いわゆる傾きと言われる係数です。
x が増えるにつれて、y がどのくらい増えていくかの、増加傾向を示すものです。
b は切片や、バイアスと呼ばれる係数です。
b は、x が 0 の時の y の値になります。
つまり、b の値が大きければ、グラフが全体的に上に押し上がり、b の値が小さければ、グラフが全体的に押し下がる形となります。
そして、x と y については、過去の実績として得られた結果が存在します。
その x と y を参考にして、傾向を示す直線の傾き a、切片 b は求められます。
尚、傾き a について、マイナスの値からプラスの値まで増やしていくと、直線は急峻な右肩下がりから、傾きが段々緩やかになっていき、最後は急峻な右肩上がりとなります。
ぐるっと直線が回転する感じです。

切片 b については、増やしていくにつれて、直線は下から上にスライドしていく形になります。
切片 b が 0 である場合には、直線は原点 (0, 0) を通る形になります。

それら、a と b の組合せを色々試してみると、以下のような形となります。

回帰分析は、これらの直線の中から、最も上手く傾向を示してくれていそうな直線を、探索し、見つけ出すアルゴリズムとなります。
回帰分析は誤差を評価して、直線を選定している
回帰分析が実現してくれている概念は、分かってもらえたかと思います。
次には、回帰分析がどうやって、直線を選定しているのかについて、説明をします。
結論から言うと、回帰分析は、誤差を評価して、直線を選定しています。
誤差とは、傾向の直線を予測値と捉えた場合の、その予測値のハズレ具合になります。
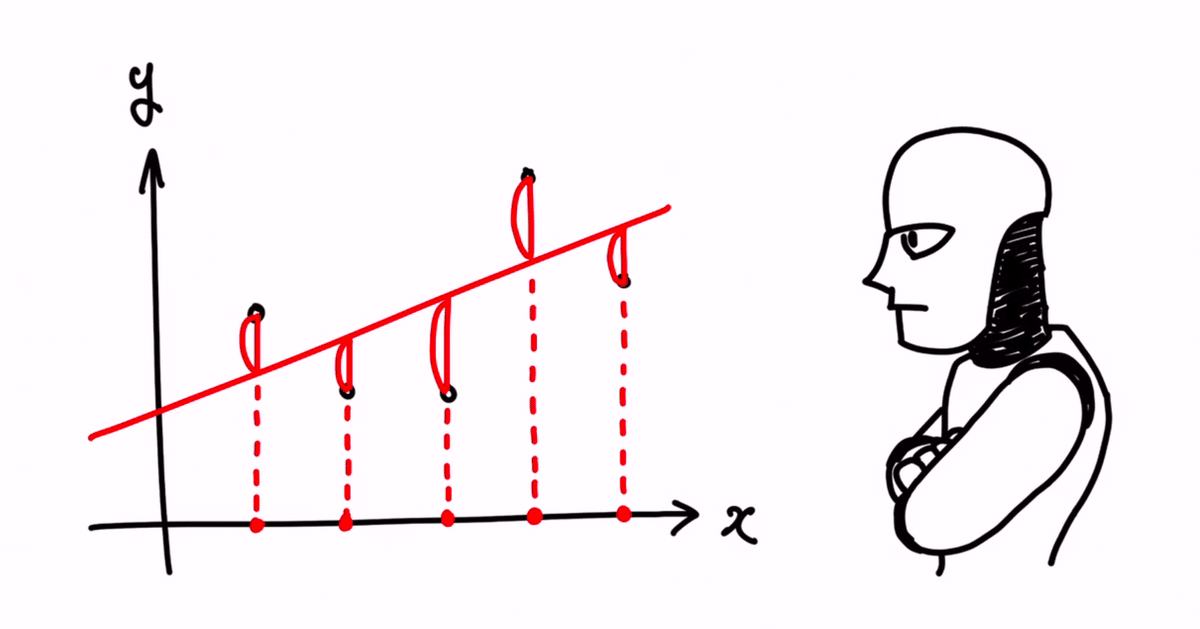
イメージとしては、以下です。

ここで、直線上の値を、ŷ = ax + b と表現することにします。
ŷ は、ワイハットと読み、y の予測値という意味です。
また、上記の黒い点は、過去の実績、つまり、既知の結果を表しているものとして、(xᵢ, yᵢ) と表すことにします。
よって、点が5つ存在する為、(x₁, y₁)、(x₂, y₂)、(x₃, y₃)、(x₄, y₄)、(x₅, y₅) という点が存在することになります。

また、そうした時に、xᵢ 上における予測値 ŷ を、ŷᵢ = axᵢ + b と表現することにします。
つまり、 yᵢ の予測値が、ŷᵢ という対応になります。

そうした時に、誤差とは、予測値と過去実績との差分になりますので、(ŷᵢ − yᵢ) と表せる形になります。
尚、誤差は、符号や向きといった概念を持たず、大きさを評価するものです。
その為、絶対値として扱うものとして、|ŷᵢ − yᵢ| という式とします。
数値として、ŷᵢ ≧ yᵢ の時、|ŷᵢ − yᵢ| = (ŷᵢ − yᵢ) であり、ŷᵢ < yᵢ の時、|ŷᵢ − yᵢ| = (yᵢ − ŷᵢ) となります。
縦棒の記号「|」で括られた値は、必ずプラスに変換するように配慮します。

回帰分析は、この誤差を評価します。
一般的には、誤差の平均、または、分散を、なるべく小さくするような、係数 a と b を探し当てようとします。
ここで、誤差の平均とは、誤差の合計値をデータ数で割ったものです。
式にすると、以下です。

これが、データが5個である場合における、誤差の平均を求める式です。
或いは、上記のような足し算の繰り返しは、Σ 記号を使うと、シンプルに表現することができます。
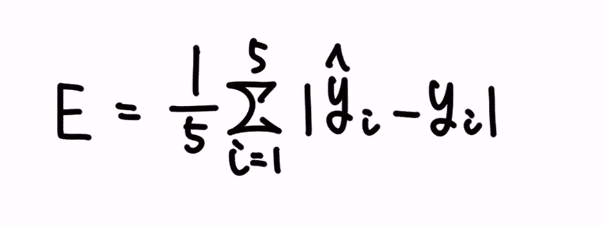
Σ 記号は、足し算を繰り返すというオペレーションを示しています。
i は、添字と呼ばれるインデックスで、データ毎に振られた番地のようなものです。
Σ 記号の下側にある「i = 1」にて、繰り返しの際に使う添字が i であり、それを 1 からカウントアップしていく、という意図が表現されています。
そして、Σ 記号の上側にある 5 は、添字のカウントアップの終了値となっています。
その為、上記ですと、i は {1, 2, 3, 4, 5} とカウントアップされていく形になります。

これが、誤差の平均の式です。
尚、式を眺めてみてもらうと分かりますが、誤差の平均を小さくすることと、誤差の合計を小さくすることは、同意となります。
平均が合計と比例している為です。
一方、分散とは、散らばりの大きさを表す指標となります。
分散の意味についてはご存知でない場合は、以下の記事が分かりやすいので、参照下さい。
一般的な、分散指標の求め方は、調査対象の値らの平均を取って、その平均を調査対象の値らから引いて、その上でそれらの値を各々2乗して、最後に合計して求める形になります。
このオペレーションは、前提として、平均値を軸に考えて、散らばりを測定することとしています。
つまり、平均値との乖離具合を、評価している形になるのです。
尚、回帰分析において、誤差の分散を求めるに当たっては、誤差の平均値は 0 として計算します。
誤差の平均値を 0 とした時、つまり、理想的な状況をベースとし、そこからの乖離の程を測定する形です。
尚、数式は、誤差の平均の式について、誤差項を、絶対値でなく2乗に変換して、出来上がりです。

尚、2乗という計算オペレーションは、必ず値がプラスになるものなので、各々の誤差を、絶対値記号で表す必要がなくなります。
という訳で、誤差の平均と、分散(誤差の平均を 0 と考えた場合の)の式が表現できました。
この2つは本質的には似ているものの、異なる結果を導き出します。
平均は、仮に、誤差の内のどれか1つが、すごく大きかったとしても、平均した誤差が小さくなりさえすれば、その大きな誤差は見過ごす形となります。
しかし、分散については、誤差を2乗するオペレーションですので、すごく大きな誤差は、2乗されて、更にとてつもなく大きなものとなってしまいます。
そうなると、平均の場合と比べて、突出するような大きな誤差を看過できなくなってしまいます。
よって、感覚的には以下です。
- 誤差の平均で評価する方針は、ある1つの大きな誤差が存在しても、看過できる余地がある
- 誤差の分散で評価する方針は、誤差の平均で評価する方針に比べ、ある1つの大きな誤差のことを、看過しずらい
尚、どちらがより正確な解を導いてくれるかは、やってみないと分かりません。
両方試して、より優秀な方を選ぶの形が望ましいです。
どうやって、直線の探索を行うか?
さて、「どの直線が良いか?」という評価基準については話をさせていただきました。
では、それをどうやって探せば良いでしょうか?
探索方法については、大きく、以下の2つが考えられます。
(1)総当り(brute-force)で探索する
(2)数学的な理論を用いて、効率良く探索する
或いは、(1)と(2)の中間にあるような考え方です。
この辺りの詳細な話は、以下の記事にも記載がしてありますので、興味があれば、参照願います。
さて、機械学習には、コンピューターの計算速度を活かして、強引に探索を行う、という基本方針があります。
問題を解く、という特徴があるものの、あまりに愚直の計算を行ってしまうと、それなりに時間がかかってしまう、という過渡期感があります。
先程、紹介した「(1)総当り(brute-force)で探索する」という方針は、正にコンピューターでも時間がかかってしまう計算方法になります。
一方で、どんな問題にも適用しやすいという利点があったりします。
総当りの対極にある考え方が、「(2)数学的な理論を用いて、効率良く探索する」という方針です。
