
機械学習の初歩、モンテカルロ法について
はじめに
皆さん、こんにちは。
今回は、機械学習の初歩技術であるモンテカルロ法についての記事を書きたいと思います。
モンテカルロ法とは
モンテカルロ法とは、機械学習の基本を抑えるのに、とても助けになるシミュレーション手法です。
コンピューターを用いた数多のシミュレーションを、乱数を用いて行うことで、現象の傾向や、確率が収束する様子を観察・分析する形です。
或いは、所望の解を探索する手法です。
まあ、要するには、シミュレーションです。
wikiに詳しい解説があります。
迷路をモンテカルロ法で解いてみる
モンテカルロ法を説明する上で、最も分かりやすい例は、迷路の探索でしょう。
先ず、それを紹介します。
例えば、以下のような迷路があったとします。
SがSTARTで、GがGOALです。
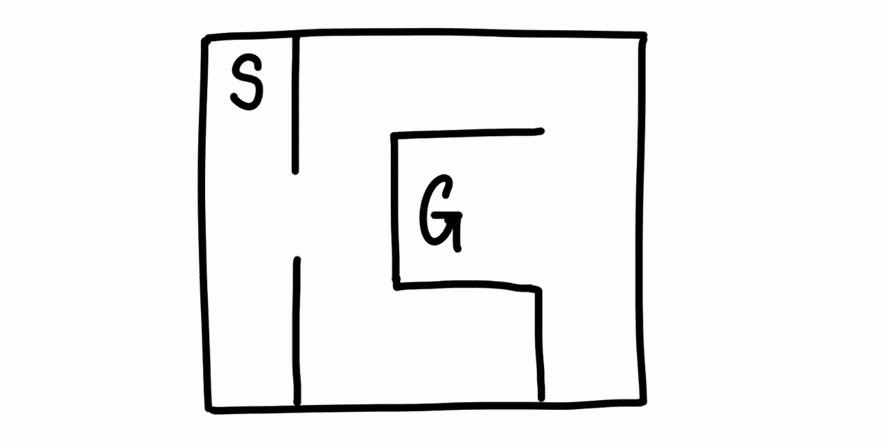
非常に、単純な迷路です。
これを人間が解こうとすれば、以下のようになります。

この位の迷路ですと、簡単に解けますね。
しかし、例えば、私の3歳の娘に、この迷路を解かせようとすると、試行錯誤を結構繰返した後、ようやくGOALへと辿り着きます。
何故、大人が簡単に迷路が解けるかというと、迷路のルールをシッカリ理解していることが1つと、脳の中でササッとシミュレーションが行える為です。
その思考に慣れているということです。
モンテカルロ法は、この手の問題を自動で解くためのシミュレーション手法です。
人間ほど高度な思考実現は難しいものの、計算の速度にモノの言わせて、愚直な思考を繰り返すことで、解の探索を試みます。
百聞は一見にしかず、ということで、先ずはシミュレーションの様子を見てもらいましょう。
以下の動画を御覧ください。

動画中、上に記載されている「step」というのは、コンピューターが迷路を解かんと、右往左往してるステップ数になります。
コンピューターは、STARTの位置から始めて、進める方向を探しながら、ランダムに上下左右に進んでいきます。
そうして、GOALが見つかったら、処理を終了します。
尚、コンピューターは、迷路を俯瞰してみることは出来ない設定で、GOALの位置はGOALに着くまで知りません。
何とも、愚直な方法ですね。
しかし、コンピューターの計算速度が早ければ、人間が解くよりも圧倒的に早く解くことができます。
例えば、上記の動画はDEMOとして可視化をしているために、処理に時間がかかっている様に見えますが、描画処理を抜きにして解くと、なんと0.1秒未満で解くことができます。
以下、プログラムを載せます。
言語は、pythonで書いています。
visualize_modeをTrueに設定するとDEMOが確認でき、Falseにすると計算にかかっている時間を正確に計測できます。
# define basic library
import numpy as np
from time import sleep
from IPython.display import clear_output
# define maze
maze = ['+-------+',
'|S| |',
'| | +-- |',
'| |G |',
'| | +-+ |',
'| | | |',
'+-------+']
# adjust maze...
for i in range(len(maze)):
maze[i] = [s for s in maze[i]]
maze = np.array(maze)
# define print state
def print_state(maze, cur_coord=None):
for vert_i in range(len(maze)):
for horz_i in range(len(maze[0])):
if (cur_coord is None):
print(maze[vert_i][horz_i], end='')
else:
if ((vert_i == cur_coord[0]) &
(horz_i == cur_coord[1])):
print('@', end='')
else:
print(maze[vert_i][horz_i], end='')
print()
# search start position and goal position
start_coord = np.where(maze == 'S')
start_coord = np.array(start_coord).T[0]
goal_coord = np.where(maze == 'G')
goal_coord = np.array(goal_coord).T[0]
# define work
wall = np.array(['|', '-', '+'])
direction = np.array([[-1, 0], # up
[0, -1], # left
[1, 0], # down
[0, 1]]) # right
# tic, toc refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# search route from start to goal
# set parameter
visualize_mode = True
random_seed = 0
# set random seed
np.random.seed(random_seed)
# set current coordinate
cur_coord = start_coord.copy()
# print state
sleep(0.1)
print('step 0')
print_state(maze, cur_coord)
sleep(0.5)
# loop of trial
tic()
for trial_i in range(1000000):
# fix direction to go
direction_tmp = direction[np.random.randint(4)]
# try to forward
next_state = (maze[cur_coord[0] + direction_tmp[0]]
[cur_coord[1] + direction_tmp[1]])
if (next_state not in wall):
cur_coord[0] = cur_coord[0] + direction_tmp[0]
cur_coord[1] = cur_coord[1] + direction_tmp[1]
# print state
if (visualize_mode == True):
sleep(0.05)
clear_output(wait=True)
print('step %d' % trial_i)
print_state(maze, cur_coord)
# judge finish or not
if (maze[cur_coord[0]][cur_coord[1]] == 'G'):
clear_output(wait=True)
print('step %d' % trial_i)
print_state(maze, cur_coord)
toc()
break人間ほど頭は良くないけど、計算が早い為、結果として人間よりも頭が良い感じになる。
これが、モンテカルロ法の肝であり、機械学習という技術分野における基本理論となります。
この原理を利用すると、例えば、ゲームのクリア方法を、コンピューターに見つけ出してもらうことも可能です。
私は趣味で、シューティングゲームなどを、モンテカルロ法でクリアすることに挑戦していたりしますが、結構うまくいきます。笑
或いは、囲碁や将棋などにて、勝つための指し方など。
Alpha Goなどの有名なAIは、モンテカルロの発展系になります。
Alpha Goとは囲碁を指すAIで、少し前に世界チャンピオンに勝利したことで有名になったものです。
詳細は、以下を参照してもらえたらと思います。
円周率をモンテカルロ法で求める
他に、モンテカルロ法で求められるものとして、円周率があります。
皆さん、円周率はご存知かと思います。
「π = 3.141592...」というやつです。
半径×半径×円周率で、円の面積が求まることは、小学校で学びますよね。
忘れていれば、思い出せば良いかと思います。
円周率をモンテカルロ法で求めるには、以下の考え方を適用します。

ランダムにダーツを投げて、以下の判定をします。
- 中心から、距離0.5以内に収まっているかどうか?
ランダム値としては、x座標とy座標の2つを生成します。
それを、ダーツが刺さった座標とします。
その上で、その座標が、上記の判定条件を満たすかどうかを判定します。
尚、正方形の面積は、1辺の長さを1とすると、「1 ✕ 1 = 1」となります。
対して、円の面積は、円周率を知っているとし、それを3.14とすれば、「0.5 ✕ 0.5 ✕ 3.14 = 0.785」となります。
その為、仮にランダムに無限のダーツを投げた場合、円の内側(上記図の「当たり」)に刺さる本数の割合は「78.5%」となります。
残る「21.5%」は、円の外側(上記図の「ハズレ」)に刺さることになります。
その考え方を逆手に取って、かつ、円の内側を中心からの距離で判定すれば、モンテカルロ法にて円周率が求まります。
それをプログラムで表現すると以下となります。
# import library
import random
import math
# refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# define method
def calc_pi(sim_num=10000):
# prep counter
inside_cnt = 0
# loop of simulation
for sim_i in range(sim_num):
# get the random value (0-1)
x = random.random()
y = random.random()
# calc Euclid distance from center
d = np.sqrt(((x-0.5)**2) + ((y-0.5)**2))
# inside or outside
if (d <= 0.5):
inside_cnt += 1
# calc pi from simulation result
p = inside_cnt / sim_num * 4
# return pi
return p
# set param
sim_num = 1000000
print('sim_num = %d' % sim_num)
tic()
# calculate pi and print
p_tmp = calc_pi(sim_num=sim_num)
print('pi = %.6f' % p_tmp)
toc()
プログラムの出力結果は、以下となります。
sim_num = 1000000
pi = 3.141064
elapsed time: 1.411354780 [sec]
試行回数1,000,000回にて、それなりの円周率が求まっています、という感じです。
計算にかかった時間は、2秒弱です。
尚、的の形を以下のような1/4円に変更すると、アルゴリズムが改善されて、少し計算速度が早くなります。

改善されたプログラムが以下です。
# import library
import random
import math
# refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# define method
def calc_pi(sim_num=1000000):
# prep counter
inside_cnt = 0
# loop of simulation
for sim_i in range(sim_num):
# get the random value (0-1)
x = random.random()
y = random.random()
# calc Euclid distance from center
d = (x**2) + (y**2) # math.sqrt((x-0)**2 + (y-0)**2) # for speed
# inside or outside
if (d <= 1):
inside_cnt += 1
# calc pi from simulation result
p = inside_cnt / sim_num * 4
# return pi
return p
# set param
sim_num = 1000000
print('sim_num = %d' % sim_num)
tic()
# calculate pi and print
p_tmp = calc_pi(sim_num=sim_num)
print('pi = %.6f' % p_tmp)
toc()プログラムの出力結果は以下です。
sim_num = 1000000
pi = 3.140220
elapsed time: 0.413794041 [sec]
精度は理論上変わりませんが、3倍強早くなりました。
総当たり(brute-force)とモンテカルロ法の違い
尚、円周率の問題については、モンテカルロ法でなくても、実は解けたりします。
例えば、x座標とy座標の組合せを、ランダムでなく計画的に配置するのです。
そのアルゴリズムで組んだプログラムは以下です。
# import library
import random
import math
import itertools
# refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# define method
def calc_pi(sim_num=1000000):
# prep counter
inside_cnt = 0
# get the random value (0-1)
coord_tmp = [(i / int(np.sqrt(sim_num))) for i in range(int(np.sqrt(sim_num)))]
xy_combi = list(itertools.product(coord_tmp, repeat=2))
# loop of x-y combi
for xy_combi_i in range(len(xy_combi)):
# set x, y
x = xy_combi[xy_combi_i][0]
y = xy_combi[xy_combi_i][1]
# calc Euclid distance from center
d = (x**2) + (y**2) # math.sqrt((x-0)**2 + (y-0)**2) # for speed
# inside or outside
if (d <= 1):
inside_cnt += 1
# calc pi from simulation result
p = inside_cnt / sim_num * 4
# return pi
return p
# set param
sim_num = 1000000
print('sim_num = %d' % sim_num)
tic()
# calculate pi and print
p_tmp = calc_pi(sim_num=sim_num)
print('pi = %.6f' % p_tmp)
toc()プログラムの出力結果は以下です。
sim_num = 1000000
pi = 3.145544
elapsed time: 0.430866241 [sec]
計算精度・速度、共に同様の結果が算出されました。
問題解決の仕様が、ランダム値よりも設計しやすいというのであれば、計画的な総当りで求めても良さそうです。
尚、総当たりのことを機械学習界隈では、よくbrute-forceと表現したりします。
尚、先に紹介した、迷路の課題も総当りでも解くことができますが、ポイントとして、何手で迷路をクリアできるかという見積もりが必要となります。
その分、分析設計がややこしくなるかもしれません。
シミュレーションと並列演算
モンテカルロ法を始めとして、シミュレーション手法は全般的に、並列演算に向いています。
シミュレーション1つ1つが独立している為に、別々のCPUを使って計算を行うと、CPU数分だけ計算速度が早くなるという話です。
尚、CPU並列演算については、以下の記事が分かりやすいです。
CPUなどの計算機構には、脳みそが複数搭載されていることが一般的です。
CPUの規格を調べた時に、コア数として表記されているものです。
その脳みその数を、上記記事ではシェフの数として表現しています。
要するに、脳みそが複数あるので、ある1つのタスクにおいても、上手く設計すれば、作業を分担して高速化できる、という訳です。
また、シミュレーションは、モンテカルロの場合、各シミュレーションの結果が、相互に影響を受けない設計が一般的ですので、シミュレーションの回数を、脳みそ毎に分担することができます。
シェフの例えで言えば、オーダー毎に、シェフを分担するような形ですね。
改めてですが、作業を並列化しない場合の速度を確認しましょう。
尚、処理回数が増えた方が、分散効果は如実に出やすいので、モンテカルロ法のシミュレーション数を先程の10倍、10,000,000回にしたいと思います。
プログラムは以下となります。
# import library
import random
import math
# refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# define method
def calc_pi(sim_num=1000000):
# prep counter
inside_cnt = 0
# loop of simulation
for sim_i in range(sim_num):
# get the random value (0-1)
x = random.random()
y = random.random()
# calc Euclid distance from center
d = (x**2) + (y**2) # math.sqrt((x-0)**2 + (y-0)**2) # for speed
# inside or outside
if (d <= 1):
inside_cnt += 1
# calc pi from simulation result
p = inside_cnt / sim_num * 4
# return pi
return p
# set param
sim_num = 10000000
print('sim_num = %d' % sim_num)
tic()
# calculate pi and print
p_tmp = calc_pi(sim_num=sim_num)
print('pi = %.6f' % p_tmp)
toc()出力結果は以下です。
sim_num = 10000000
pi = 3.141370
elapsed time: 4.035185099 [sec]
先程、シミュレーション実施した時よりも、シミュレーション回数が10倍増えていますので、処理時間もおよそ10倍かかっています。
上記が、CPUの並列処理をしていない計算速度です。
次に、CPUの並列処理をする場合です。
私のパソコンには、コアが2つ搭載された「Dual-Core Intel Core i5」が積んであるので、2並列処理が実施可能です。
それでは、2並列処理を実施してみます。
プログラムは以下です。
# import library
import random
import math
# for multi CPU
from multiprocessing import Pool
# refer from [https://qiita.com/daenqiita/items/be92e332fb029bacd795]
import time
def tic():
#require to import time
global start_time_tictoc
start_time_tictoc = time.time()
def toc(tag="elapsed time"):
if "start_time_tictoc" in globals():
print("{}: {:.9f} [sec]".format(tag, time.time() - start_time_tictoc))
else:
print("tic has not been called")
# define method
def calc_pi(sim_num=10000):
# prep counter
inside_cnt = 0
# loop of simulation
for sim_i in range(sim_num):
# get the random value (0-1)
x = random.random()
y = random.random()
# calc Euclid distance from center
d = (x**2) + (y**2) # math.sqrt((x-0)**2 + (y-0)**2) # for speed
# inside or outside
if (d <= 1):
inside_cnt += 1
# calc pi from simulation result
p = inside_cnt / sim_num * 4
# return pi
return p
# define method for multi thread
def through_darts(sim_num):
# prep counter
inside_cnt = 0
# loop of simulation
for sim_i in range(sim_num):
# get the random value (0-1)
x = random.random()
y = random.random()
# calc Euclid distance from center
d = (x**2) + (y**2) # math.sqrt((x-0)**2 + (y-0)**2) # for speed
# inside or outside
if (d <= 1):
inside_cnt += 1
# return inside count
return inside_cnt
# prep thread
sim_num = 10000000
thread_num = 2
# start watch
tic()
# calculate pi on multi thread
with Pool(thread_num) as pool:
inside_cnt = pool.starmap(through_darts,
[tuple([int(sim_num/thread_num)]) for i in range(int(thread_num))])
# stop watch
toc()
# print inside count
print(inside_cnt)
#
print(sum(inside_cnt) / sim_num * 4)出力結果は以下です。
elapsed time: 2.081275940 [sec]
[3926095, 3927103]
3.1412792
少し、プログラムの書き方が複雑になります。
プログラムの書き方が複雑になる点は、並列化処理のデメリットと言えます。
処理速度としては、並列処理を行っていない時の4秒と比べて、2倍の2秒とシッカリ高速化されています。
並列化がしやすいタスクについては、この様にハッキリとした高速化を実現することが可能です。
尚、CPUの中には、コアがもっと沢山搭載されているものもあり、それですと更なる高速化が期待できたりします。
pythonとC/C++言語
尚、ここまで紹介したプログラムは、pythonで書かせてもらっていますが、実は、pythonはfor文が苦手という弱点があります。
pythonのスクリプト上で、「for i in range(n):」などと書いて、繰り返す処理を実施すると、速度が遅くなってしまうのです。
その為、先程紹介したプログラムなどは、あくまで実験用として捉えてもらえると良いかと思います。
尚、速度が遅くなる、というのは、別のプログラミング言語と比較して、ということなのですが、例えば、C/C++言語などと比較すると如実です。
C/C++言語とは、省メモリ・高速化が実現しやすい言語となっています。
ただし、その長所と引き換えに、実装がかなり難しくなります。
対して、python言語は、非常に直感的なコード構成で、実装がしやすいという長所があります。
一方で、処理速度は遅くなりがちな面があります。
ただし、numpyなどのライブラリを上手く使用すると、処理速度の問題は緩和できたりします。
numpyによる処理速度緩和については、以下の記事を参考にしてもらえたらと思います。
(numpyに関する記事を書く)
ちなみに、上記の記事にも書いてありますが、pythonは実はC/C++言語を、コードの深いところで使用しています。
pythonは、C/C++言語をラッピングしている形になっているのです。
つまり、プログラムの深いところは、C/C++言語でプログラミングがされていて、それがpythonコードから呼び出されている形です。
さて、そんなpythonと密接な関係にあるC/C++言語、そして、pythonよりも高速なC/C++言語ですが、どのくらい早いのでしょうか。
試してみましょう。
以下、C/C++言語のプログラムとなります。
typedef signed char int8;
typedef signed short int16;
typedef signed int int32;
typedef signed long long int64;
typedef unsigned char uint8;
typedef unsigned short uint16;
typedef unsigned int uint32;
typedef unsigned long long uint64;
#include "stdio.h"
#include "stdlib.h"
#include <random>
#include <time.h>
int32 main()
{
int32 i, sim_num, inside_cnt;
double x, y, d;
sim_num = 100000000;
inside_cnt = 0;
srand((unsigned)time(NULL));
for(i = 0; i < sim_num; i++)
{
x = rand() / (double)RAND_MAX;
y = rand() / (double)RAND_MAX;
d = sqrt((x * x) + (y * y));
if(d <= 1.0){
inside_cnt++;
}
}
printf("pi = %.10f\n", ((double)inside_cnt / (double)sim_num / (0.5 * 0.5)));
}
pythonと文法が大分違いますが、大体やっていることは同じだと、理解できるかと思います。
ただ、文法の縛りなどが強く、やはりpythonよりは書きづらいです。
例えば、変数を最初に定義しなくてはならないなど、制約が強いのです。
そして、このプログラムの出力結果は以下となります。
# g++ montecalro.cpp -o montecalro
# time ./montecalro
pi = 3.1414458000
real 0m5.160s
user 0m5.105s
sys 0m0.019s
上の2行は、コンパイルコマンドと、実行コマンドになります。
処理時間は、約5秒かかっていますが、これは100,000,000回のシミュレーションをした結果となっています。
pythonの際は、10,000,000回のシミュレーションで4秒ほどかかっていましたので、大体10倍弱程の高速化がされています。
アルゴリズムが全く同じにも関わらず、言語が違うだけで、処理速度が10倍近く変わってしまう、という訳です。
尚、C/C++言語でも、CPU並列化は実現できます。
CPU並列化を実施しているC/C++言語のプログラムは以下となります。
typedef signed char int8;
typedef signed short int16;
typedef signed int int32;
typedef signed long long int64;
typedef unsigned char uint8;
typedef unsigned short uint16;
typedef unsigned int uint32;
typedef unsigned long long uint64;
#include "stdio.h"
#include "stdlib.h"
#include <random>
#include <time.h>
#include <omp.h>
int32 main()
{
int32 sim_num, inside_cnt;
int32 thread_num;
sim_num = 10000000;
inside_cnt = 0;
thread_num = 2; //omp_get_max_threads();
printf("thread_num = %d\n", thread_num);
srand((unsigned)time(NULL));
#pragma omp parallel num_threads(thread_num)
{
int32 thread_i;
thread_i = omp_get_thread_num();
printf("thread_i = %d\n", thread_i);
#pragma omp for reduction(+:inside_cnt)
for(int32 i = 0; i < sim_num; i++)
{
double x, y, d;
x = rand() / (double)RAND_MAX;
y = rand() / (double)RAND_MAX;
d = sqrt((x * x) + (y * y));
if(d <= 1.0){
inside_cnt++;
}
}
}
printf("pi = %.10f\n", ((double)inside_cnt / (double)sim_num / (0.5 * 0.5)));
}プログラムの出力結果は以下です。
# g++ -std=c++14 -fopenmp montecalro_omp.cpp -o montecalro_omp
# time ./montecalro_omp
thread_num = 2
thread_i = 0
thread_i = 1
pi = 3.1403928000
real 0m3.284s
user 0m3.775s
sys 0m2.564s
CPU並列化前は、5秒と少しかかっていた処理が、3秒と少しで終わるようになりました。
キッチリ倍という訳ではありませんが、高速化が実現されました。
機械学習への発展例、連立方程式の自動解答
さて、機械学習の初歩であるモンテカルロ法を紹介しました。
基本的には、コンピューターの計算速度を活かして、何かしらの解を探索するという手法になります。
尚、モンテカルロ法が機械学習の初歩だというのは、探索が単純な為です。
本腰入れた機械学習の世界は、もう少し探索に工夫が凝らされています。
特に、その探索の方針に、数学・統計学・物理学等々の考え方が適用されています。
その辺りは、連立方程式をモンテカルロ法っぽく(どちらかと言うと、総当たり的に)解いている記事を別で書いていますので、そちらも参考にしていただけたらと思います。
おわりに
以上で、モンテカルロ法の紹介を終えます。
ここまで読んでくださった方、本当にありがとうございました。🙇
