ガウス過程って結局なんなのか？

　正規分布からスタートしてガウス過程のおおよそを理解することを目的に記事を書きました。正規分布がどんな分布かなんとなく知っていれば理解ができると思います。

ガウス過程の定義

　多変量正規分布に従う確率変数の集合です。

　一応定義も書いておきましたが、定義だけではイメージがつきにくいとは思うので、詳しく見ていってみましょう。

まずは正規分布から

　ガウス過程はその名前が示す通りガウス分布（正規分布）と密接な関係にあります。そのため正規分布がどのようなものなのかを知ることは重要です。

　正規分布にはパラメータが2つあります。これはつまり2つのパラメータが決まればその分布を記述（表現）することができるということです。
　その2つのパラメータとは、（1変数の場合）
　　・平均（期待値）
　　・分散
です。
　確率変数が多変数の場合は、平均も変数の分だけ増えますので、
　　・μ：平均ベクトル
　　・Σ：共分散行列（分散共分散行列）
がパラメータです。

ガウス過程の解釈

ガウス過程を正規分布のように表記するとこちらになります。

　ガウス過程は、m(x)とk(x)によって分布を表現することができます。これらは式の形が示しているように関数です。
　　・m(x)：平均関数
　　・k(x)：共分散関数
　この2つの関数の名前は正規分布のパラメータとよく似ています。正規分布との最大の違いは、正規分布がベクトル or 行列であったのに対して、ガウス過程は関数になっている点です。その点が違うだけで、基本的には正規分布と同じと考えることができます。（これはつまり、ガウス過程は正規分布を一般化したものと見ることができます。）

　したがって、m(x)とk(x)に入力であるxを代入すると平均ベクトルと共分散行列が求まりますので、あとはそれらをパラメータとして正規分布からサンプリングすればよいのです。なお、入力xはガウス過程においては時間がよく用いられます。つまり、出力f(x)は時間の関数、時系列です。

Pythonのコードで実際にサンプリングしてみる

　実際にコードを書いて動作を実験してみるとよくわかります。
　まずは正規分布（1変数）です。以下は正規分布からデータをサンプリングするコードです。正規分布は2つのパラメータがありますので、平均を0、分散（標準偏差）を1と設定し、正規分布から5,000個サンプリングしています。

########################
## gaussian distribution
#########################

# parameter
mu = 0
sigma = 1

# sample size
sample_size = 5000

# draw samples from gaussian distribution
x = scipy.stats.multivariate_normal.rvs(mean=mu, cov=sigma, size=sample_size)

　このコードをガウス過程に拡張します。ガウス過程では平均と分散が関数になっているのでした。そこで今回は以下の関数を用いることにします。

（余談ですが、この共分散関数をRBF;Redial Basis Functionと呼びます）

　ガウス過程は入力であるxをそれぞれの関数に代入して平均ベクトルと共分散行列を算出し、正規分布でサンプリングするだけです。コード化してみると意外にシンプルです。

#########################
## gaussian process
#########################

# index(input)
x = np.arange(-5., 5., 0.2)

# mean function
f_m = lambda x: 0.25 * x **2

# covariance function
f_k = lambda x1, x2: np.exp(-0.5 * (x1 - x2) ** 2)

# mean vector
m = f_m(x)

# covariance matrix
k = np.array([[
   f_k(x1, x2)
   for x2 in x]
   for x1 in x])

# draw samples from gaussian distribution
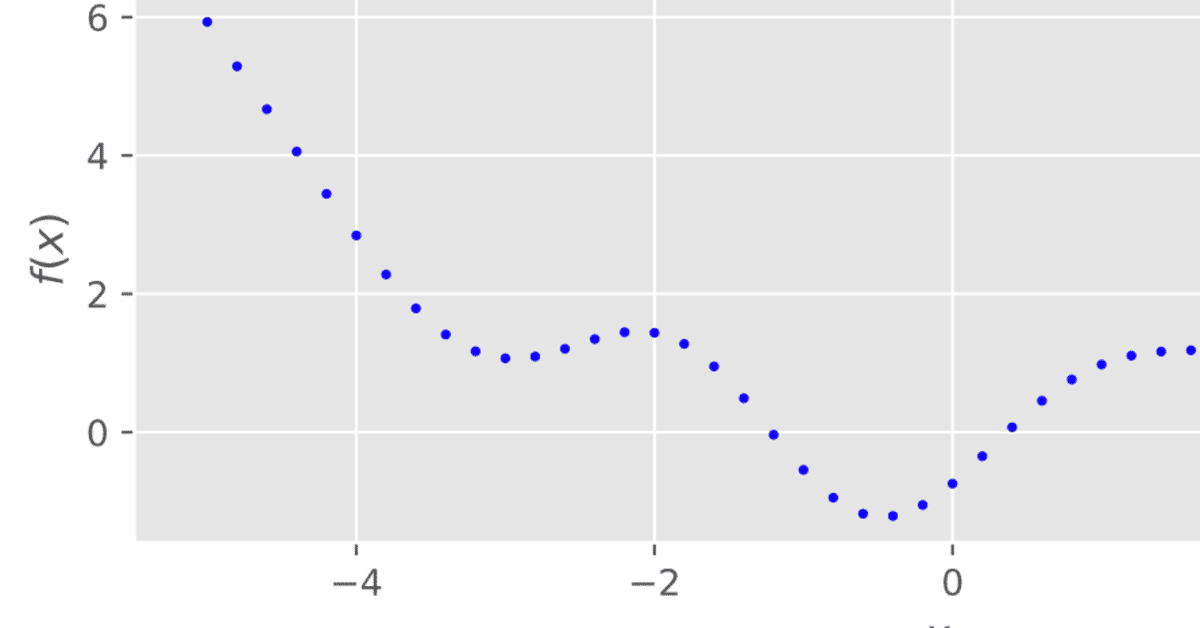
f = scipy.stats.multivariate_normal.rvs(mean=m, cov=k, size=1)

これをプロットすると以下になります。

　x軸は時間であると考えることができ、ガウス過程は変数の時系列的な変化を記述することができます。変数の各時点同士の関係が正規分布になっています。

　以上がガウス過程の基本です。ポイントは
　　・平均と分散が（時間の）関数
　　・関数から平均と分散が算出できたら正規分布からサンプリングするだけ
です。

今回の実験で作成したnotebookは以下のとおりです。

参考文献

１．Carl Edward Rasmussen, "Gaussian Processes in Machine Learning"
２．Carl Edward Rasmussen and Christopher K. I. Williams, "Gaussian Processes for Machine Learning"