ポアソン分布の確率母関数と期待値

ポアソン分布の概要

ポアソン分布は、ある一定の時間間隔において、事象が発生する回数の確率を表す分布です。事象が発生する回数が確率変数Xになります。確率分布を表す確率質量関数は下式です。

分布のパラーメータはλ(λ>0)です。これは一般に強度と呼ばれるもので、一定の時間間隔で事象が発生する平均の回数を表しています。たとえばλ=3のときのグラフは以下のようになります。平均(λ)が３ですから、3周辺の確率が比較的高くなっていることがわかります。

確率質量関数の和が1になることの証明

これには以下のeのマクローリン展開を用います。

ポアソン分布の確率の和が1になるのは、上のマクローリン展開を用いれば下式のようになります。二項分布の和の範囲は試行回数nまでであるのに対して、ポアソン分布は発生回数は無限まで（ほぼゼロですが）あることに注意してください。

確率母関数

次は確率母関数ですが、こちらにもeのマクローリン展開を用います。

モーメント母関数

確率母関数を求めているので容易に求められます。

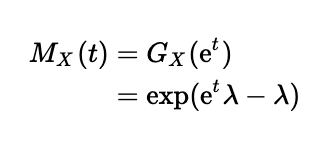
期待値と分散

期待値と分散は上で求めた確率母関数またはモーメント母関数から求めることができますが、比較的確率母関数からの方が容易です。まず期待値からです。期待値は確率母関数をsで微分し、sに1を代入することで求まります。

そもそも平均回数がλであることを考えると、期待値が一致するのは当然な結果と言えそうです。続いて分散です。まずは2階微分し、

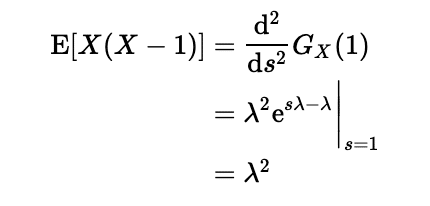
分散を求める公式を用いると

となります。期待値も分散もλとなりました。期待値と分散が等しいことはポアソン分布の特徴と言えます。

参考文献

現代数理統計学の基礎（久保川達也）