
マルコフの不等式をわかりやすく
期待値から大きく外れるような観測値が得られることは、ほとんどあり得ないと直感的にわかりますが、マルコフの不等式はこれを数学的に記述したものになります。
マルコフの不等式を導く
まずは以下のグラフを見てみます。

Xを非負の確率変数、cを非負の任意の定数とします。このとき破線(青色)と実線(赤色)は以下の式で表されます。

いわゆる、破線はステップ関数、実線は恒等関数です。
確率変数の和を考えたとき、破線は常に実線の下側にありますので
![]()
p(i)をiが生起する確率とすると期待値は

左辺はX≧cの確率にcをかけたもの、右辺は実線のXの期待値なので

これがマルコフの不等式です。
実際に使ってみる
理解するためには実際に使ってみるのが一番です。まずは指数分布の例で試してみます。
Q.指数分布(λ=1)について、X≧aの確率をマルコフの不等式で考える。
指数分布(λ=1)のX≧aの確率は下図の網掛けの面積です。

この値は積分すればわかるのですが、マルコフの不等式を用いることで簡単におおよその範囲を導くことができます。
まず、期待値を求めます。指数分布の期待値は1/λです。
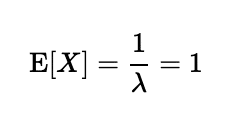
これをマルコフの不等式に代入すると

このマルコフの不等式が示すのは、X≧aの真の確率は1/a以下であるということです。本当でしょうか?では、真の確率はどうなるのか、実際に計算してみます。

不等式が成立しているかはグラフ化することでわかります。
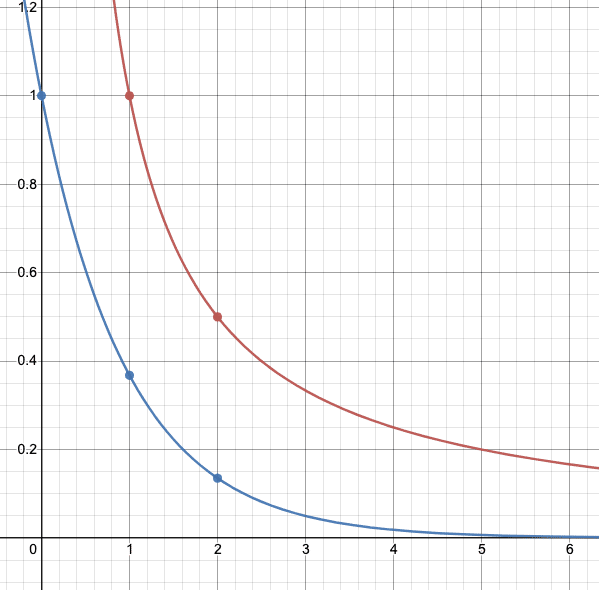
青色が真の確率(e^-a)、赤色がマルコフの不等式の確率(1/a)です。非負のaにおいては青色が常に下側に来るので、マルコフの不等式が成立していることがわかります。
これはマルコフの不等式が上界を示していることになります。

年収の例
年収は非負(年収がマイナスというのは考えにくい)な確率変数なのでマルコフの不等式が適用できます。たとえば、平均年収が5倍以上の人の割合を考える場合、c=5E[X]をマルコフの不等式に代入すると

よって、平均年収が5倍以上の人の割合は多く見積もっても20%であると推定できます。
参考
新装改訂版現代数理統計学(竹村彰通)
現代数理統計学の基礎(久保川達也)
Wikipedia Markov's inequality
The Markov Inequality, MIT OpenCourseWare
The Markov and Chebyshev Inequalities, Stanford Ben Lynn
