幾何分布の確率母関数と期待値
幾何分布の概要
幾何分布は成功の確率がpのベルヌーイ試行を独立に行っていき、初めて成功するまでの失敗の回数の分布です。失敗の回数が確率変数になります。確率分布を表す確率質量関数は下式です。
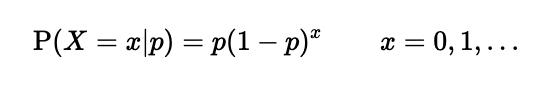
成功確率pに対して失敗の確率は(1-p)であり、x回失敗し1回成功するのでこのような数式になります。分布のパラメータは成功する確率pです。なお、幾何分布の表現方法はもう一つあり、初めて成功するまでの試行回数を確率変数とするものもあります。この場合の確率質量関数は下式です。
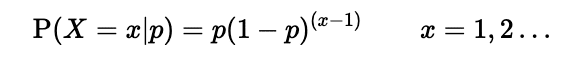
どちらを用いても本質は同じです。以降では前者の形式を用いていきます。
たとえば、成功確率p=0.3のとき、幾何分布は以下のようなグラフになります。
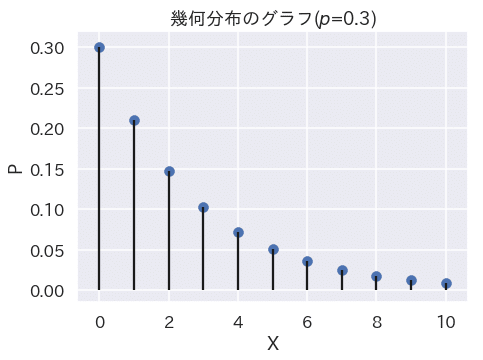
幾何分布という名前について
幾何分布という名前はちょっと変わっていますね。この名前の由来なんですが、幾何分布の確率の順序が等比数列であることから来ています。等比数列は英語で"geometric sequence"と言い、幾何分布は"geometric distribution"です。幾何的な数列の性質を持っているから幾何分布と言うようです。
確率質量関数の和が1になることの証明
これには無限等比級数の和の公式を用います。初項がa、公比|r|<1のとき以下が成り立ちます。
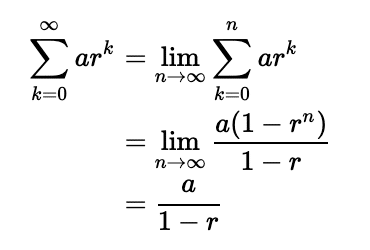
1行目から2行目は等比数列の和の公式を用いています。これを使えば、
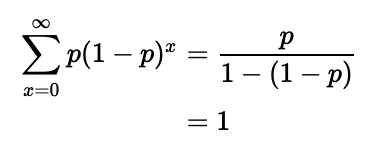
というように、しっかり"1"になります。
確率母関数
こちらにも無限等比級数を用います。
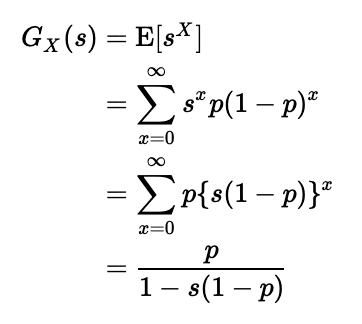
モーメント母関数
確率母関数を求めているので容易に求められます。
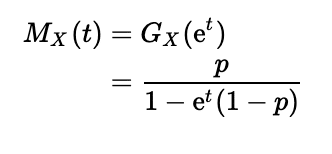
期待値と分散
期待値と分散は上で求めた確率母関数またはモーメント母関数から求めることができますが、比較的確率母関数からの方が容易です。まず期待値からです。期待値は確率母関数をsで微分し、sに1を代入することで求まります。
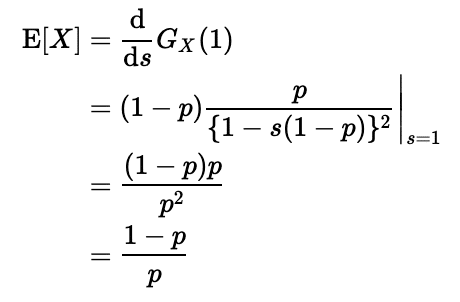
続いて分散です。まずは2階微分し、
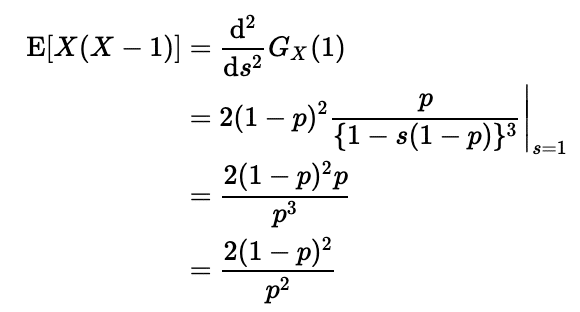
分散を求める公式を用いると
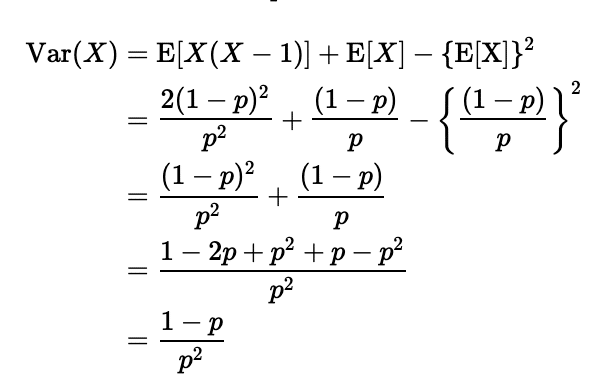
参考文献
・現代数理統計学の基礎(久保川達也)
・"Wikipedia" Geometric distribution
・"高校数学の美しい物語" 無限等比級数の収束,発散の条件と証明など
