現代数理統計学の基礎の演習問題（2章問4）：MSEとMAEの最小化

2021年5月30日 10:48

現代数理統計学の基礎（久保川達也）の演習問題、2章問4を問いてみました。

問題

この問題を解釈すると、前者はMSE(Mean Squared Error)、後者はMAE(Mean Absolute Error)について、それぞれを最小化する推定量は何かというものです。これらの評価基準は機械学習でも頻繁に見られるものですが、そんな問題が何気なく出ていることが興味深いです。

まずはMSEですが、これはtで微分して0と置いてtについて解けばよいです。

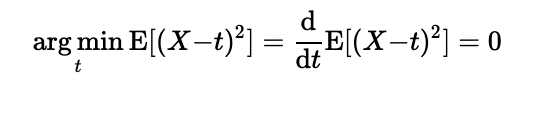
実際に計算すると

よって

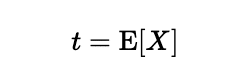
MSEを最小にする推定量は期待値（平均値）であることがわかりました。

次はMAEです。まずは期待値の定義から次のように書けます。

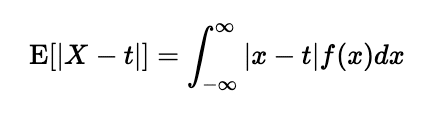
絶対値があると扱いにくいので外すことを考えます。
x−tが正になるためには以下の2パターンが考えられます。

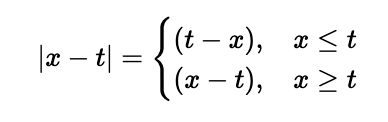
1つ目はxがt以下である場合で、これはt-xとすることで常に正になります。2つ目はxがt以上である場合で、これはx-tとすることで常に正になります。
したがいまして、xがtを境にして条件が変わることになりますので、この条件を用いることで積分の範囲を分けることができます。

この式を最小化することを考えますので、微分して0と置き解きます。

微分と積分が混在した複雑な式になりますが、ライプニッツの積分法則を使うことで整理することができます。（wikipediaリンクの4つ目の式）
それぞれの項を整理していきます。

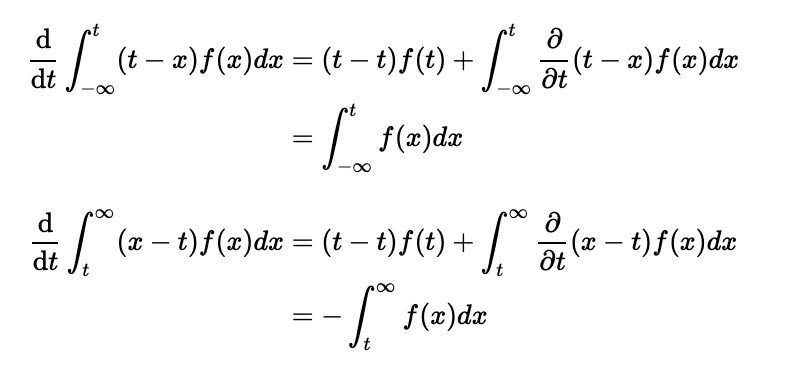
これらを元の式に代入すると

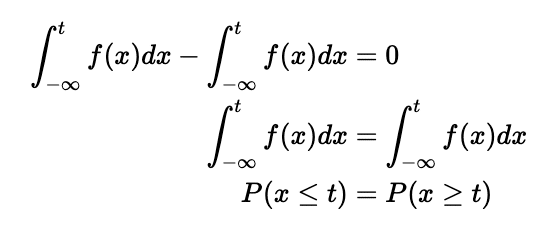
最後の式変形は確率密度関数の積分は確率（累積分布関数）になるためです。
ところで、確率の定義から以下が成り立ちますので（xがt以上になる事象とxがt以下になる事象は全事象なので確率は1になる）

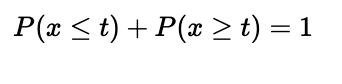
したがいまして

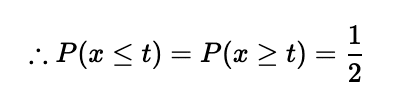
確率（累積分布関数）が1/2になるtは、その定義から中央値です。よてMAEを最小にする推定量は中央値と求まりました。