電験3種 2021年度 理論 問7 直流回路

内部抵抗のある電源による最大出力電力についての問題です。簡単な解き方があるのですがそれは(解法2)に回して,まずは正攻法で解いてみます。
(前提)抵抗で消費される電力
抵抗に電流を流したときに消費される電力P [W]は,電圧V [V],電流I [A],抵抗R [Ω]として,
P=V×I……⓵
P=R×I^2……②
P=V^2 / R……③
で表せます。②③は,⓵にオームの法則V=R×I,または,I=V/Rをそれぞれ代入したものです。
⓵~③どれを使ってもいいのですが,状況に応じて,問題文で与えられている文字や簡単に求められる文字の入った式を使うのがいいでしょう。
(解法1)正攻法
可変抵抗で消費される電力をP [W]とすると,
P=R×I^2……⓵
となります((前提)の3式どれでもいいですが,とりあえず問題文に出てくるRとIを使った式にしました)。Pを大きくするには,RとIの両方を大きくすればいいのですが,抵抗Rを大きくすると電流Iは小さくなってしまいます。
例えば,Rを∞[Ω]にすると電流は流れないのでIは0 [A]となり,P=0 [W]になります。一方,Iが最大になるのは抵抗Rが0 [Ω]の時なので,やっぱりP=0 [W]になってしまいます。
R,Iともにほどほどの時,Pが最大になるようです。
Pを求めるために,RとI,2つの文字を使っているので話がややこしくなっています。RとIには関係があるので,その関係を式で表し,どちらか1つの文字でPを表せば,中学校で習うような関数の最大値を求める問題になります。
どちらの文字で表してもいいのですが,最後に求めたいのがIなので,「R=Iの式」の形で関係を表し,これをP=R×I^2に代入してRを消すことにしましょう。
Iの式と書きましたが,E, r, nも問題文で与えられた決まった値=答えにそのまま使える文字なので「R=I, E, r, nの式」ということになります。
可変抵抗にかかる電圧をV [V]として,可変抵抗についてオームの法則の式を立てると,
R=V/I……②
となります。
ここで,Vは電池全体の電圧と等しいので,電池の方を考えます。
電池1個あたりの起電力はEですが,外に出てくる電圧は内部抵抗による電圧降下を差し引いたものになります。
この回路の電流はどこでもI [A]なので,内部抵抗r [Ω]による電圧降下はrI [V]となり,電池1個当たりの電圧はE-rI [V]になります。
この電池n個が直列につながっているので,電池全体の電圧(=可変抵抗にかかる電圧)V [V]は,
V=n×(E-rI)……③
となります。
ここからは数学の問題です。
③を②に代入して,
R=n×(E-rI)/I
これを⓵に代入して,
P=(n×(E-rI)/I)×I^2=n×(E-rI)×I……④
さらに計算(分配)すると,
P=-nrI^2+nEI……④’
となります。

④’を見ると,二次関数で,I^2の係数が負なので,Pは上に凸のグラフ(放物線)になります。

④の式をよく見ると,I=0の時と,E-rI=0の時(つまりI=E/rの時),P=0となるようです。これを踏まえてグラフを描くと次の図のようになります。

I=0の時とI=E/rの時にP=0となり,上に凸のグラフです。
放物線は対称なので,Pが最大となるのはIがちょうど真ん中の時,つまり,
I=(0+E/r)÷2=E / 2r
の時で,答えは④になります。
この問題では聞かれていませんが,もし最大出力を聞かれたら④式にI=E / 2rを代入,可変抵抗の大きさを聞かれたら②式にI=E / 2rと③式を代入すればいいでしょう。
お疲れさまでした。
(解法2)電源の内部抵抗と最大出力電力
(解法1)の正攻法でももちろん答えにたどり着けますが,結構時間がかかってしまうと思います。
知っておくと簡単に解ける知識があります。それは,
電源の内部抵抗と同じ大きさの外部抵抗をつないだ時,外部抵抗で消費される電力が最大になる。
ということです。
この問題では,電池全体の起電力はn×E [V],内部抵抗は合わせてn×r [Ω]なので,可変抵抗Rが内部抵抗と同じn×r [Ω]の時に可変抵抗で消費される電力が最大になります。
この時,回路に流れる電流I [A]は,電池の起電力に内部抵抗と外部抵抗が直列につながっているので,
I=n×E /(n×r+n×r)=n×E /(2×n×r)=E / 2r
となります。
簡単ですね。
(蛇足1)電源の内部抵抗と最大出力電力(証明1)
(解法2)で,
電源の内部抵抗と同じ大きさの外部抵抗をつないだ時,外部抵抗で消費される電力が最大になる。
と書きましたが,本当かどうかたしかめてみましょう(計算が面倒なので,電池は1個にしました)

外部抵抗で消費される電力 P [W]は,
P=R×I^2……⓵
(解法1)と同様にRを消去してIを求め,求まったIからRを求めてもいい(後述する突然の変形がないのでその方がわかりやすいかもしれません。蛇足2にて)のですが,今回はRについて知りたいので,Iを消去してみたいと思います。
回路全体でオームの法則を使うと,
I=E /(r+R)……②
②を⓵に代入して,
P=R×(E /(r+R))^2
=R×E^2 /(r+R)^2
=R×E^2 /(r^2+2rR+R^2)
=E^2×R/(r^2+2rR+R^2)
=E^2×1/(r^2/R+2r+R)

ここで,Eはあらかじめ与えられた定数(変わらない)なので,Pを最大化するには残りの部分1/(r^2/R+2r+R)が最大になればよく,1/(r^2/R+2r+R)を最大化するには,分母のr^2/R+2r+R……③が最小になればいいということになります。
ここで突然ですが,(r/√R-√R)^2……④について考えます。
(r/√R-√R)^2=(r/√R)^2-2×(r/√R)×√R+(√R)^2
=r^2/R-2r+R……④’
③と④’を比較するととよく似ています。③=④’+4rになっています。④’は④を変形しただけなので,
③=④’+4r
=④+4r
=(r/√R-√R)^2+4r

rは定数なので,③を最小化するには残りの部分(r/√R-√R)^2が最小になればよく,2乗なので最小になるのはかっこの中の部分がr/√R-√R=0……⑤の時になります。
⑤より,
r/√R-√R=0
両辺に√Rをかけると,
r-R=0
r=R
ということで,外部抵抗で消費される電力Pが最大になるのは内部抵抗rと外部抵抗Rが等しいときだということがたしかめられました。
ちなみに,このとき流れる電流は,②式にr=Rを代入して,
I=E /(r+R)=E /(r+r)=E/2r
外部抵抗で消費される電力 P [W]は,⓵式にr=RとI=E/2rを代入して,
P=R×I^2=r×(E/2r)^2=r×(E^2 / 4r^2)=E^2 / 4r
になります。
(蛇足2)電源の内部抵抗と最大出力電力(証明2)
電源の内部抵抗と同じ大きさの外部抵抗をつないだ時,外部抵抗で消費される電力が最大になる。
を,いったんRを消去してIを求め,求めたIを使ってRを求めるという手順で証明してみます(解法1と同様の手順です)

外部抵抗で消費される電力 P [W]は,
P=R×I^2……⓵
外部抵抗にかかる電圧をV [V]とすると,
V=E-rI
なので,外部抵抗についてオームの法則で
R=V/I
=(E-rI)/ I……②
②を⓵に代入して,
P=((E-rI)/ I)×I^2
=(E-rI)×I
Pは,I=0の時と,E-rI=0の時(つまりI=E/rの時)にP=0となる,上に凸の放物線なので,Pが最大となる時のIは,I=0とI=E/rの真ん中で,
I=(0+E/r)÷2=E / 2r……③
③を②に代入して,
R=(E-r×(E / 2r))/(E / 2r)
=(E-(E / 2))/(E / 2r)
=(E / 2)/(E / 2r)
=r
ということで,Pを最大化するのは,R=rの時だと証明できました。
(蛇足3)変域
(解法1)(蛇足2)で電流Iと消費電力Pのグラフを描くと,Pが負になってい部分があります。これは何でしょうか? 消費電力が負ということは,発電しているのでしょうか?
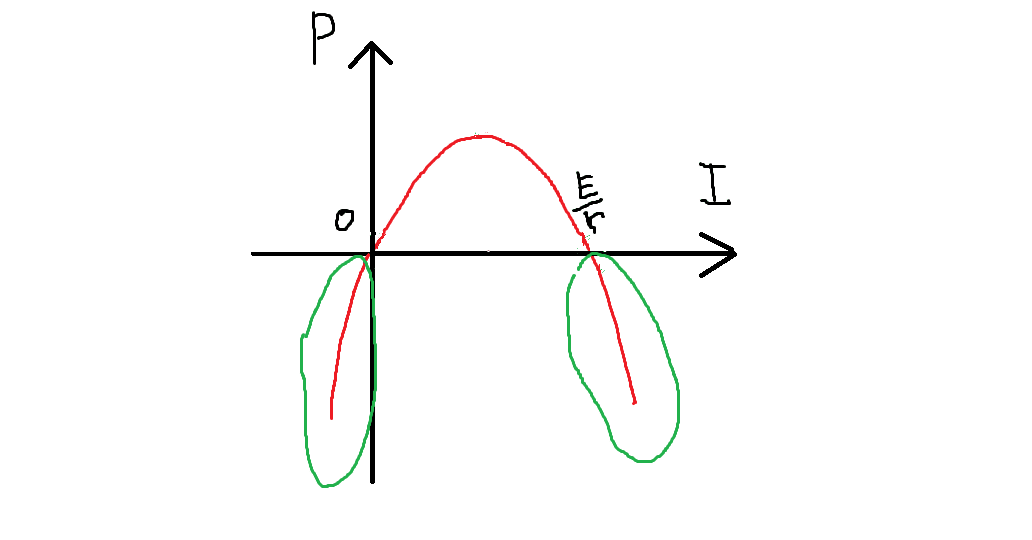
結論から言うと,この領域になることはありません。
なぜなら,この問題で自由に変えられるのは可変抵抗R [Ω]ですが,Rはどんなに小さくても0Ω(負にはならない)でその時の電流Iは電池の内部抵抗によりnE/nr=E/r [A]であり,逆にRをどんなに大きくしてもIは0より小さくはならないからです。
もしこの問題が記述式なら,「Iのとりうる値の範囲(値域)は0≦I≦E/rであり,その範囲での最大値を求める」と書くか,求まったIの時のRを求めてIが現実にありうることを確認するのが数学的には厳密です。
