電験3種 2021年度 理論 問14 ブリッジ回路

ブリッジ回路についての問題です。

（前提）ブリッジ回路とは

抵抗の大きさを測るには，抵抗に電源をつないで抵抗にかかる電圧の大きさと流れた電流の大きさを測り，オームの法則で求めるのが一般的です。しかし，電圧や電流の測定には誤差が伴い，それらを使って計算した抵抗値にも誤差が生じます。
一方，電流が流れたか流れていないかだけであれば，電流の大きさがどれくらいかに比べて精密に求めることができます。これを利用して，抵抗の大きさを精密に求めるのがブリッジ回路です。

ブリッジ回路では，測定対象の抵抗の他に，すでに抵抗値がわかっている抵抗2つと抵抗値を変化させられる可変抵抗1つ，そして電流が流れたか流れていないかを精密に測定できる検流計を使います。
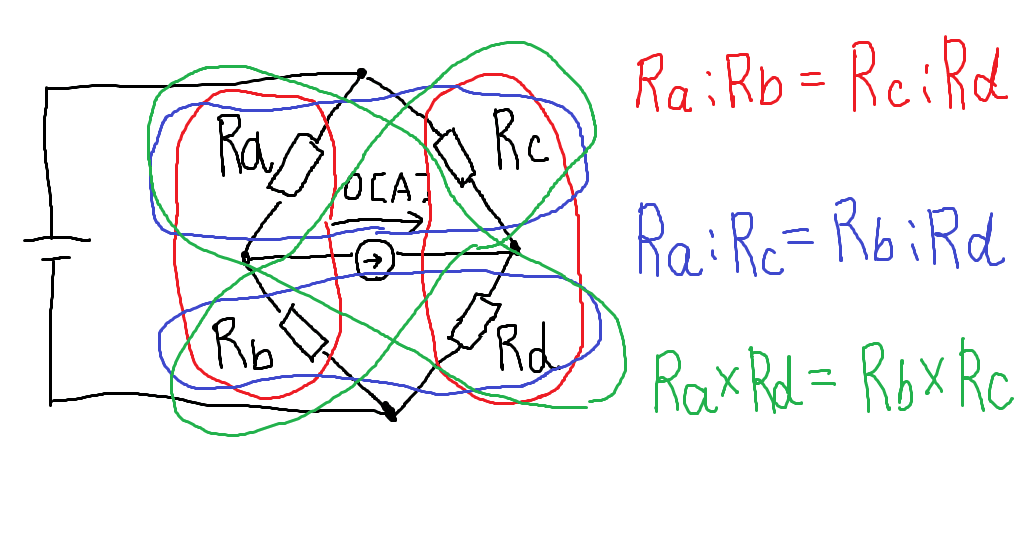
4つの抵抗と検流計を図のように電源につなぎます。検流計に電流が流れないように可変抵抗を調整すると，
　Ra：Rb＝Rc：Rd
となり，この式のうち3つの抵抗は分かっているので，測定対象の抵抗を求めることができます（どうしてこの式が成り立つかは蛇足1参照）

（誤差を考慮しないときのRx）

誤差を考慮しないで求めたRxは，ブリッジ回路の式より，
　R1：R2＝Rx：R3
　R1×R3＝R2×Rx
　Rx＝R1×R3/R2……⓵
となります。

ちなみに，ブリッジ回路と電源の間に抵抗r [Ω]がありますが，ブリッジ回路の式に影響はありません。抵抗rの電圧降下の分ブリッジ回路にかかる電圧は下がりますが，そもそもブリッジ回路の式は電圧にかかわらず成り立つからです。

（誤差を考慮したときのRx）

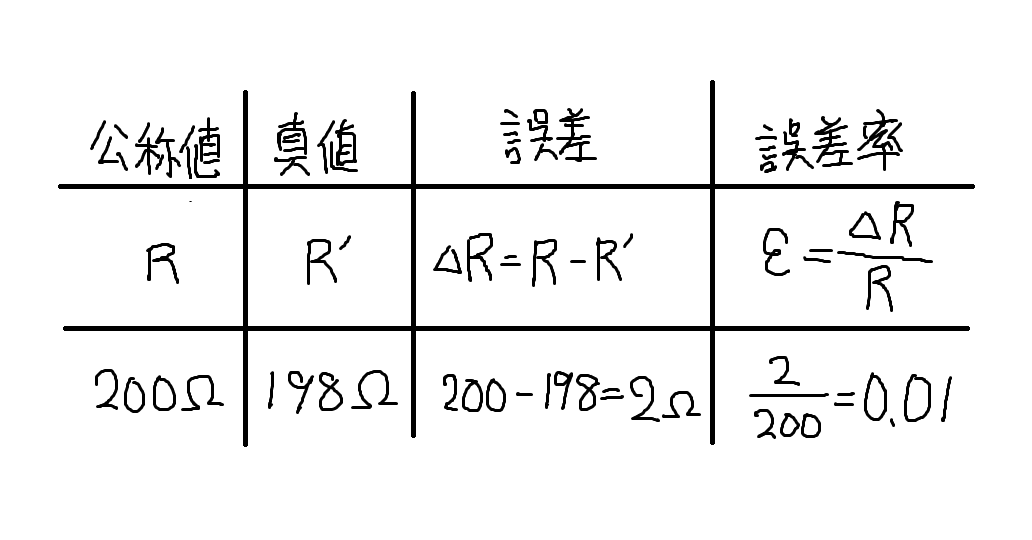
「Rkの真値からの誤差ΔRk……誤差率εk＝ΔRk/Rkが……0.01」とは，どういうことでしょうか？

例えば200Ωと書かれている抵抗（公称値200Ω）があったとします。この抵抗を厳密に測ってみたところ198Ωでした。
このとき，Rk＝200 [Ω]，真値は198 [Ω]となり，真値からの誤差ΔRk＝200-198＝2 [Ω]，誤差率εk＝ΔRk/Rk＝2/200＝0.01となります。
もし真値がわかる前に200Ωという値を使って何かを計算していたら，その計算結果には誤差が含まれています。200Ωの部分を198Ωに置き換えて計算しなおせば，正しい計算結果が出ることになります。

それでは，R1～R3の真値を求め，それを使ってRxの真値を求めましょう。
ΔRk＝Rk－（Rkの真値）なので，（Rkの真値）＝Rk-ΔRkです。
つまりR1 [Ω]だと思っていた抵抗は，実はR1－ΔR1 [Ω]でした。
ここで誤差率ε1＝ΔR1/R1＝0.01なので，ΔR1＝0.01×R1となります。
したがって真値はR1－ΔR1＝R1＋0.01×R1＝0.99×R1 [Ω]となります。
同様にして，R2の真値は1.01×R2 [Ω]，R3の真値は0.98×R3 [Ω]となります。

Rxの真値をR’xとして，これらの抵抗値で⓵式を置き換えると，
　R'x＝（0.99×R1）×（0.98×R3）/（1.01×R2）
　　　≒0.961×R1×R3/R2
となり，誤差は，
　ΔRx＝Rx－R'x
　　　＝R1×R3/R2－0.961×R1×R3/R2
　　　＝0.039×R1×R3/R2
誤差率は
　εx＝ΔRx/Rx
　　＝（0.039×R1×R3/R2）/（R1×R3/R2）
　　＝0.039
ということで，最も近いのは⑤の0.04になります。

（蛇足1）ブリッジ回路の式

ブリッジ回路の式，Ra：Rb＝Rc：Rdを導いてみましょう。

ブリッジ回路で検流計に電流が流れないということは，Raに流れた電流は分岐せずにそのままRbに流れるということです。
Raに流れる電流をI1とすれば，Rbに流れる電流もI1です。同様に，Rcに流れる電流をI2とすれば，Rdに流れる電流もI2になります。

検流計に電流が流れないということは，検流計に電流を流そうとする力，すなわち検流計両端の電位差がない（電圧が等しい）ということでもあります。

RbとRdの下側は導線でつながっているため電圧は等しく，検流計両端の電圧も等しいので，それぞれの抵抗による電圧降下が等しいということになります。それぞれの抵抗にオームの法則を使うと，
　I1×Rb＝I2×Rd
　I1＝I2×Rd÷Rb……⓵
となります。同様に，RaとRcによる電圧降下も等しいので，
　I1×Ra＝I2×Rc
　I1＝I2×Rc÷Ra……②
となります。

⓵＝②＝I1なので
　I2×Rd÷Rb＝I2×Rc÷Ra
両辺をI2でわって，
　Rd÷Rb＝Rc÷Ra
両辺にRa÷Rdをかけて（※），
　Ra÷Rb＝Rc÷Rd
　Ra：Rb＝Rc：Rd
ということで，ブリッジ回路の式を導けました。

（※）のところで，Ra÷Rdをかけましたが，これはRa：Rb＝Rc：Rdの式を導くための意図的なものです。この式を日本語で説明すると「ブリッジ回路の左右の回路それぞれで，上下の抵抗の比が等しいとき，検流計に電流が流れない」ということになります。
ここで，Ra÷Rdをかける代わりに，両辺を逆数にして，左辺と右辺を入れ替えるとRa：Rc＝Rb：Rdとなります。日本語にすると「ブリッジ回路の上下それぞれで，左右の抵抗の比が等しい」でしょうか。
もう一つ，Ra×Rbをかけると，Ra×Rd＝Rb×Rcとなります。日本語だと「対角線上にある抵抗の積が等しい」ですね。

単に式の変形をしただけで，本質的には全部同じなので，どれで覚えても問題ないです。個人的にはRa：Rb＝Rc：Rdが検流計両端の電位差がないということを表しているようで好きですが，Ra×Rd＝Rb×Rcが覚えやすくて間違いにくいかもしれません。