NIRSの信号処理について考えてみる〜②HPFとLPF〜

2025年2月3日 23:41

サンプルデータ

心理学の実験ではブロックデザインという一定の周期で刺激を呈示するデザインを採用することがあるが，この場合は刺激に対する脳の応答も周期的なものになる。ゆえに，計測時間と刺激呈示の時間間隔から脳応答がおよそ何 Hz の成分になるのかを予想することができる。

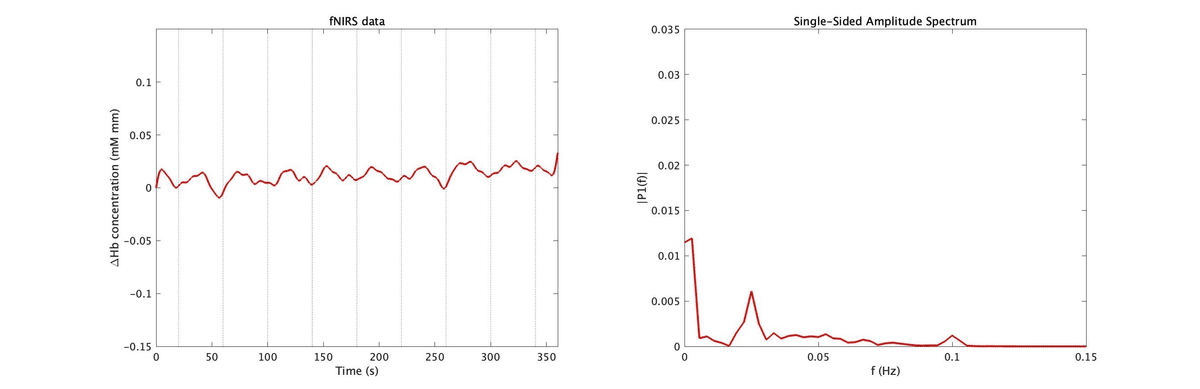
ここでは，「Rest (20 秒) → Task (20 秒)」という流れを 9 回繰り返したブロックデザインを想定したデータに，ノイズ除去の結果をわかりやすくするために線形トレンドと 0.1 Hz（振幅 0.02）の正弦波を加えたものをサンプルデータとする（図1）。

ここからは MATLAB のコードも記載するため，手元にデータがある場合は参考にされたい。その場合は，本記事のデータとは異なるものであると思われるが，「対象のデータ（oxy-Hb）」「時間情報」「サンプリング周波数」の 3 つがあれば同じように進めることができると思われる。

data = readmatrix('sampleData.csv');  % サンプルデータ

time = data(:, 1);  % 1 列目にある時間情報を抽出
oxy = data(:, 2);  % 2 列目にある oxy-Hb データを抽出
fs = 1/time(2, :);  % サンプリング周波数(ここでは 55.556 Hz)

なお，図1は以下のようなコードで作成することができる。なお，図1の縦波線は刺激呈示のタイミングを示すが，自作の関数を使用しているためここでは省略する。

plot(time, oxy, 'r');
axis tight
ylim([-0.2 0.4])
xlabel('Time (s)'); 
ylabel('\DeltaHb concentration (mM mm)');
title('fNIRS data');

サンプルデータでは 360 秒の中で 9 回の周期的な反応が得られることが期待されるため，脳の応答成分は 0.025 Hz だと予想することができる。ゆえに，0.025 Hz よりも低い周波数成分と高い周波数成分を除去することが求められる。

ここで，サンプルデータに含まれる周波数成分を調べてみる。付与したノイズと脳の応答成分が含まれていることがわかる（図2）。ここではフーリエ変換を行っているが，これについては次の記事で解説する。

なお，図2は以下のようなコードで作成することができる。

x = oxy';

L = length(x);
win = hann(L)';  % ハン窓を使用

xWin = x.*win;  % 窓関数の畳み込み

acf = 1/(sum(win)/L);  % Amplitude Correction Factor の算出

Y = fft(xWin);  % 高速フーリエ変換
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = fs*(0:(L/2))/L;

plot(f, P1*acf, 'r', 'LineWidth', 2)
title('Single-Sided Amplitude Spectrum')
xlabel('f (Hz)')
ylabel('|P1(f)|')
xlim([0 0.15])
ylim([0 0.07])

ハイパスフィルタで低周波成分を除去

まずは，ハイパスフィルタ（HPF）を使って応答成分よりも下の周波数成分を除去する。

ハイパスフィルタの設計には様々な方法があるが，ここでは "fir1" という関数を使用してフィルタを作成する [1]。ここでは次数を 3200，遮断周波数を 0.01 Hz とした（次数の設定理由は後述）。

HPF = fir1(3200, 0.01/(fs/2), 'high');
oxy_H = filtfilt(HPF, 1, oxy);

freqz(HPF, 1)  % フィルタの周波数応答を確認（図5を参照）

作成したフィルタを関数 "filtfilt" で適用すると，ドリフト補正ができていることがわかる（図3）。ただし，元のデータに含まれていた約 0.005 Hz 未満の成分の振幅が大きかったため，これの減衰には成功したが完全に取り除くことはできなかった。

これは，フィルタは遮断する周波数成分を完全に取り除くのではなく，その成分を減衰させるに留まるためである。なお，遮断周波数の周辺にもフィルタの影響が出ることにも注意されたい（図4）。

なお，今回のハイパスフィルタでは次数を 3200 としたが，これはサンプルデータで十分なドリフト補正ができるものを探した結果，適当な次数が 3200 程度であったためである。具体的には，"fir1" で設計したフィルタは遮断周波数における正規化ゲインが –6 dB（遮断周波数の部分の振幅を 0.5 倍にする）となるが [3]，設定した遮断周波数が極めて小さなものであったためか –6 dB の減衰を得るために次数を 3200 まで上げる必要があったいうものである（図5）。

ローパスフィルタで高周波成分を除去

次に，ローパスフィルタ（LPF）を使って応答成分よりも上の周波数成分を除去する。

手順は HPF とほぼ同じである。関数 "fir1" でフィルタを作成し，作成したフィルタを HPF を適用したデータに適用する。ここでは次数を 500，遮断周波数を 0.07 Hz とした。

LPF = fir1(500, 0.07/(fs/2));
oxy_HL = filtfilt(LPF, 1, oxy_H);

作成したフィルタを関数 "filtfilt" で適用すると，高周波成分がある程度取り除かれていることがわかる（図6）。

フィルタ適用後の手続き

実際に NIRS データを解析する場合は，フィルタ適用後にブロックごとのデータを切り出してベースライン補正，加算平均，標準化を行う。本記事ではフィルタの適用に焦点を当てたため，これらの手続きについては割愛する。これらの手順については小野先生のテキスト [1] などを参照されたい。

線形トレンドの除去について

上の LPF 適用後の波形が示す通り，本記事の方法では線形トレンドが除去しきれていないという問題が残っている。

これは，サンプルデータの応答成分の周波数が 0.025 Hz と極めて小さいものであることに加えて，トレンド成分が応答成分よりも小さく，さらにこれが応答成分に近い周波数であることが影響していると思われる。ゆえに，サンプルデータのトレンド補正には HPF では力不足であると考えられる。

トレンド補正を目的とした HPF の代替案として，MATLABが持つ関数 "detrend" が挙げられる。これの使用は HPF よりも容易であるが，"detrend" の場合は低周波成分を減衰させるのではなく線形トレンドを除去するという点には注意されたい（線形トレンド以外の低周波成分を考慮すると，"detrend" と HPF を併用してもよいかもしれない）。

以下に "detrend"の使用例を示す。第3引数（"on"）でブレークポイントを指定しているが [4]，これまでの図の縦波線同様に刺激が呈示されたタイミングがこれに該当する。

oxy_dt = detrend(oxy, 'linear', on)  % 第3引数は必須ではない

結果を見ると，線形トレンドが消えていることがわかる（図7）。

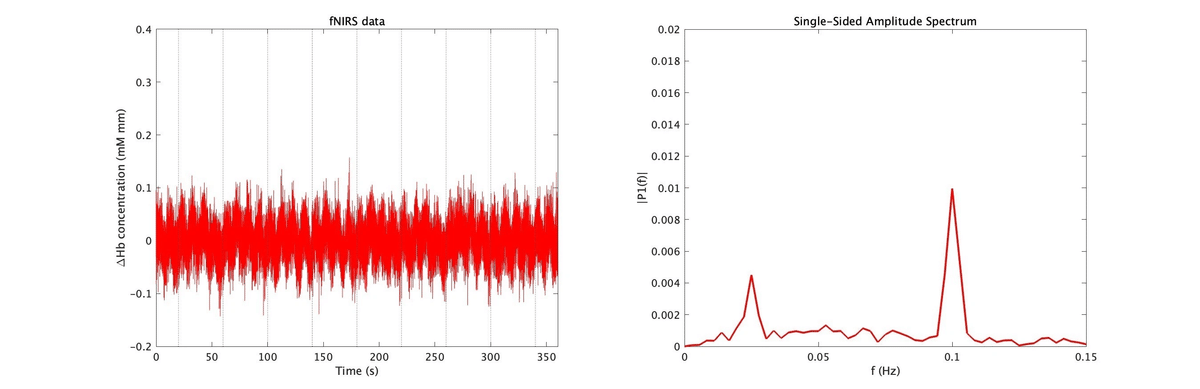
なお，図7にさらに LPF を適用すると以下のようになる（図8）。

図8　detrend + LPF 適用後の波形（左）とこれに含まれる周波数成分（右）

引用・参考文献

[1] 小野弓絵 (2018) MATLABで学ぶ生体信号処理，コロナ社，pp112-113
[2] しなぷすのハード制作記　「カットオフ周波数の解説」https://synapse.kyoto/glossary/cutoff_frequency/page001.html (2023年3月13日)
[3] MathWorksヘルプセンター fir1 https://jp.mathworks.com/help/signal/ref/fir1.html (2023年3月13日)
[4] MathWorksヘルプセンター detrend https://jp.mathworks.com/help/matlab/ref/detrend.html (2023年3月13日)